Task01 分治
Pow(x,n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25
说明:
-100.0 < x < 100.0
n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。
解题思路:幂函数也就是将x与相乘n次,可以直接使用for循环暴力求解,时间复杂度为O(n),下面思考如何将其优化,一般比O(n)还快的为O(logn),那么就要思考有什么算法是可以达到O(logn)的,我们可以想到x10其实是x5的平方,而x5是x2的平方再乘一个x,以这种方式可以使复杂度降为O(logn)。至于特殊情况,n为0时返回1,n为负数时计算的是倒数,可以把n取反得正后计算再取倒数。
方法一:递归
这里使用【快速幂算法】,本质是分治算法
当幂的次数是偶数时,比如说x^64,可以按照:
![]()
的顺序,从x开始,每次把上一次的结果平方。
当幂的次数为奇数时:
![]()
在计算偶次幂时还是直接把上一次的结果平方,在计算这些奇次幂时,把上一次的结果平方后还需要再乘上一个x。
如果从左往右看,我们并不知道下一次的结果需不需要额外乘一个x,但如果从右往左看,分治的思想就很明显了:
1.计算x^n时,先递归计算出m = ⌊n/2⌋,y = x^m,其中⌊⌋表示向下取整;
2.根据递归的结果,如果n为偶数,那么y^2,反之 y^2 * x;
3.递归边界为n = 0,任意数的0次方均为1。
class Solution:
def myPow(self, x: float, n: int) -> float:
def quickMul(N):
#0次幂返回1
if N == 0:
return 1.0
#递归处理
y = quickMul(N//2)
return y * y if N % 2 == 0 else y * y * x
#n为正数正常计算,n为负数计算的是倒数
return quickMul(n) if n > 0 else 1.0 / quickMul(-n)
时间复杂度:O(logn),即递归的层数
空间复杂度:O(logn),即递归的层数,因为递归时函数调用使用栈空间
方法二:迭代
上述的递归需要额外使用栈空间,可以试着将递归转写为迭代。我们从左往右找一下规律,看看哪些地方需要额外乘一个x,以x^77作为例子:
![]()
这里把需要额外乘上x的步骤打上了+标记,发现:
1.最初的x在后续的操作中被平方了6次,即 x^64
2.x^4 到 x^9中额外乘的x后续被平方了3次,即 x^8
3.x^9 到x^19中额外乘的x后续被平方了2次,即 x^4
4.x^38 到 x^77中额外乘的x后续没有被平方,即x
将上述每一步的结果称为贡献,将这些贡献相乘,x^64 * x^8 * x^4 * x = x^77。而这些贡献的指数部分恰巧是2的幂次,因为每次额外乘上的x都会在后续被平方若干次,而指数1,4,8,64恰好对于77的二进制(1001101)中的每个1。
因此借助整数的二进制拆分,可以得到迭代计算的方法,一般地,若整数n的二进制拆分为:

那么:
![]()
所以我们可以将x不断平方,得到x2,x4,x^8…,再计算n的二进制表示,如果n的第k个(从左往右,从0开始计数)二进制位为1,则将对应的结果计入答案。
class Solution:
def myPow(self, x: float, n: int) -> float:
def quickMul(N):
ans = 1.0
#初始贡献为x
x_contribute = x
while N > 0:
#进行二进制拆分,当前二进制位为1时,将贡献计入答案
if N % 2 == 1:
ans *= x_contribute
#将贡献不断进行平方
x_contribute *= x_contribute
#判断后舍弃二进制表示的最低位,每次循环只需判断最低位
N //= 2
return ans
return quickMul(n) if n > 0 else 1.0 / quickMul(-n)
时间复杂度:O(logn),即对n进行二进制拆分的时间复杂度
空间复杂度:O(1)
最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
当年的笔试题 现在还是不会
解题思路:
法一:动态规划
设nums数组的长度为n,下标从0到n-1
a_i表示nums[i],f(i)表示以第i个数结尾的【连续子数组的最大和】,那么我们要求的答案是:
也就是求出每一个位置的f(i),返回f数组中的最大值即可,对于f(i-1)和a(i),我们希望获得一个较大值,动态规划转移方程为:
步骤:
每加入一个元素就比较一次,pre维护当前最大值
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
maxAns = nums[0]
pre = 0
for x in nums:
pre = max(pre + x, x)
maxAns = max(maxAns, pre)
return maxAns
动态规划还有另一种较直观的做法:如果上一个值大于0,则与当前值相加。比如 [-2,1,-3,4,-1,2,1,-5,4]:
[-2]为第一个值;
[-2,1],上一个值小于0,不做改变
[-2.1.-2],上一个值为1大于0,将其与-3相加等于-2
[-2,1,-2,4],上一个值小于0,不做改变
[-2,1,-2,4,3],上一个值为4大于0,将其与-1相加得到3
[-2,1-2,4,3,5],上一个值为3大于0,将其与2相加得到5
[-2,1,-2,4,3,5,6],上一个值为5大于0,将其与1相加得到6
[-2,1,-2,4,3,5,6,-1,4],-5上一个值为6大于0,将其与-5相加得到-1,;4上一个值小于0不做改变。
此时取数组中最大值6为输出。
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
for i in range(1, len(nums)):
if nums[i-1] > 0:
nums[i] += nums[i-1]
return max(nums)
方法二:分治(没看懂)
多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
解题思路:分治。如果a是数组nums的众数,那么将nums分为两部分,那么a至少是其中一部分的众数(反证法可证)。因此可以使用分治的思想,将数组分为左右两部分,分别求出两边的众数,再确定最终的众数。
使用分治算法递归求解,直到所有的子问题都是长度为1的数组,其中的数即为众数;若回溯后某区间的长度大于1,则将左右子区间的值合并,如果这两部分的众数相同,该值即为众数,否则比较两个不同的众数出现的次数,大的为最终的众数。
class Solution:
def majorityElement(self, nums, low=0, high=None):
def majority_element_rec(low, high):
# 当数组只有一个元素时,该数即为众数.
if low == high:
return nums[low]
# 切片为左右部分,然后递归.
mid = (high - low) // 2 + low
left = majority_element_rec(low, mid)
right = majority_element_rec(mid+1, high)
# 两边的众数相同,该数即为众数.
if left == right:
return left
# 否则,比较两个众数的出现次数.
left_count = sum(1 for i in range(low, high+1) if left == nums[i])
right_count = sum(1 for i in range(low, high+1) if right == nums[i])
return left if left_count > right_count else right
return majority_element_rec(0, len(nums)-1)
时间复杂度:O(nlogn),函数majority_element_rec()求解2个长度为n/2的子问题,并做两遍长度为n的线性扫描,分治的时间复杂度为:
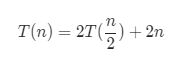
时间复杂度可以表示为:

此处的a为子问题数量,n/b为每个子问题的规模
空间复杂度:O(logn),递归使用了额外的栈空间,算法每次将数组分为两部分,需要进行logn次递归。
