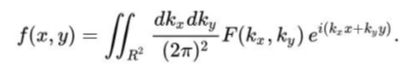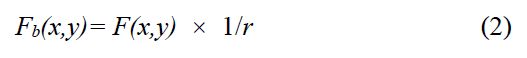CT图像重构方法详解——傅里叶逆变换法、直接反投影法、滤波反投影法

绪

      在做CT图像处理的时候遇到很多问题，对于滤波反变换有许多细节存在疑问，经过多天查找资料和利用MATLAB程序一步步实现后终于豁然开朗，于是想要总结成文，作为笔记方便今后查看。文中若有错误欢迎指出！

      CT图像的形成和重构，在数学上的描述分别为拉东变换和拉东反变换。简单点说，拉动变换是用于描述通过X射线扫描物体形成CT图像这个过程的一种数学表示，而拉东反变换描述的则是对CT投影数据进行重构，还原成物体图像的一种数学方法。本文章主要讲的是CT图像重构的方法，也就是拉动反变换的具体实现方法，当然可能也有小伙伴想了解一下什么是拉动变换，这里贴上传送门：拉东变换。

而拉东反变换在数学上的表达式如下：

由公式可看出拉东逆变换在数学上实际上是一个二维傅里叶逆变换，但由于二维傅里叶逆变换计算量大，耗时长，因此计算机对于拉东逆变换的具体实现方法主要为反投影法，反投影法又分为直接反投影法和滤波反投影法。由此可见CT重构方法主要为以下三种：

（1）傅里叶逆变换法

（2）直接反投影法

（3）滤波反投影法

下面具体看下这三种图像重构方法。

 

---

  （1）傅里叶逆变换法

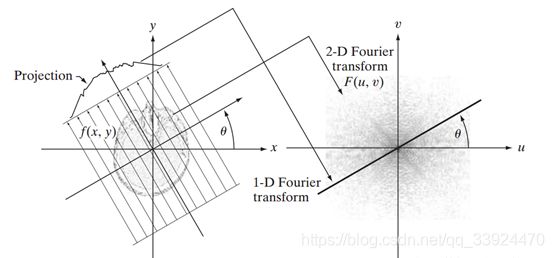
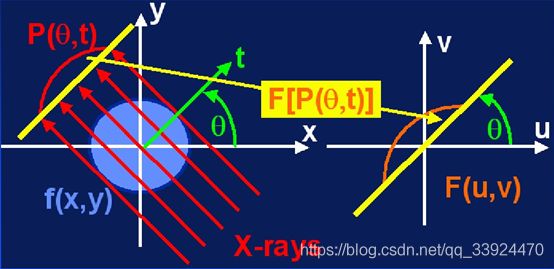
该方法基于一个重要的定理：中心切片定理。

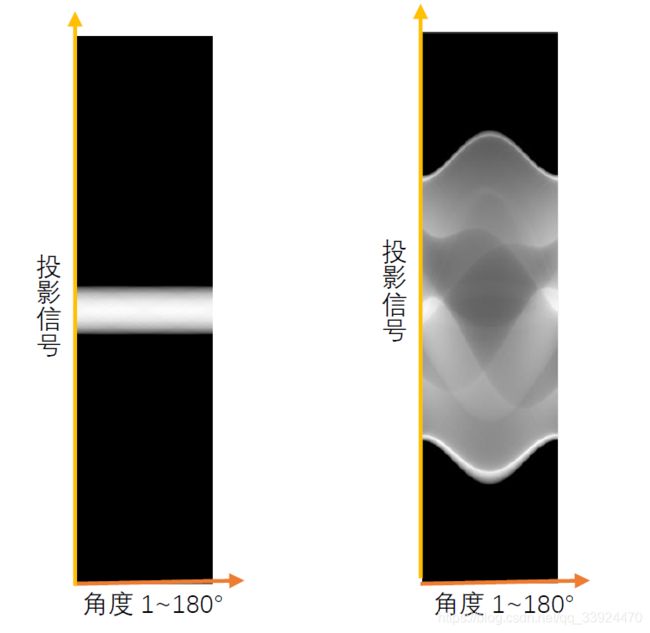
该定理简单地理解就是：通过角度为θ扫描得到的投影，该投影的一维傅里叶变换，与对整个图像二维傅里叶变换后，二维频域中对应θ角度的一个切片信号是相同的，下面两个图理解起来更直观。

图1

图2

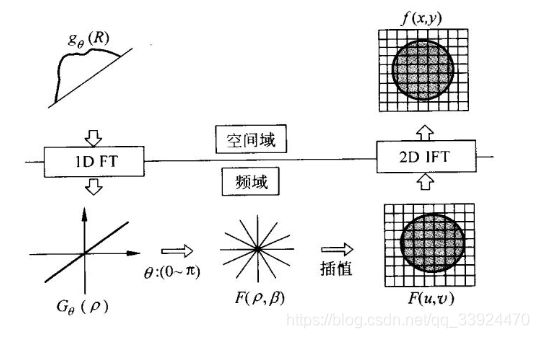
根据该理论，傅里叶逆变换法可以简单分成以下步骤：

① 假设每旋转1°就扫描一次，当对物体扫描了180°之后，我们就能得到180个投影信号（就是180根投影线）→在临床上，若使用平行扫描CT，我们拿到手的数据就是这个（在数学上，就是对图像进行拉东变换）

② 对180个投影信号进行一维傅里叶变换

③ 对②得到的180个一维频域信号，根据相对应的扫描角度，在空间中旋转排列，拼成一个二维频域空间（如图3）

④ 由于数据是离散的，直接按照角度进行排列难以铺满整个二维空间，因此还需要对空缺的地方进行插值（一般三次样条插值效果最好），但插值会带来一定误差。另外，由于中心的信号密集，周围的信号稀疏，显然会损失一部分高频数据，造成高频信号失真，这就是采用傅里叶逆变换法重构图像时会使得图像边缘模糊的原因。

⑤ 对④中拼接而成的二维图像进行二维傅里叶逆变换，就可重构原图

图3  傅里叶逆变换法

该方法的缺点有：

a/高频信号有所失真

b/在插值时还涉及到极坐标和直角坐标的变换，计算量大

c/需要用到二维傅里叶逆变换，总体耗费时间长

由于计算机处理二维傅里叶逆变换的计算量太大，因此很少直接使用该方法实现拉东逆变换。

 

（2）直接反投影法

反投影法的原理是将所测得的投影值，按照其原投影路径，平均地分配到经过的每一个点上，把各个方向的投影值都这样反投影后，在把每个角度的反投影图像进行累加，从而推断出原图。为方便理解，下面分别用两张图，通过MATLAB编程来还原一下该过程（程序在最后）：

原图如下：（图1简单，图2复杂）

①首先看一下图像经过拉东变换（即CT扫描）后的数据（图中每一列代表对应每一个角度的投影信号，在这里只是拼起来成一张图了）

②对每个角度的信号进行反投影（选了几个代表性角度）：

② 把以上角度发反投影图像叠加起来：

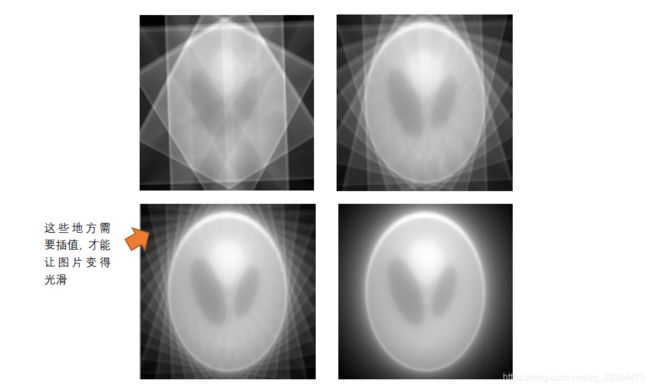
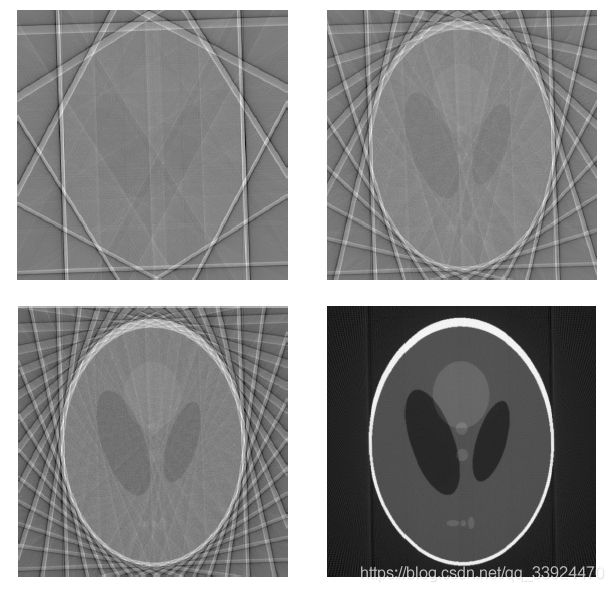
当越来越多的反投影图像加起来之后，可以看到：

到此，直接反投影法结束。值得注意的是，由于反投影图是离散叠加的，显然在中心处信号集中，边缘处信号稀疏，因此在最后需要在空缺的地方进行插值，才能得到最终的原图像。上面演示的过程中没有进行插值，仅仅是把反投影图叠加，因此能够看出每一张图都不是很光滑。

从以上过程可以很直观地看出直接反投影法出现伪迹的原因：

①在“回抹“过程中（就是把投影信号平均到每个二维空间点的过程中），会把原图像本来是0的像素点也”抹“上一个平均值，最终使得重构的图像中存在误差；

②插值过程中会带来误差，且周围信号稀疏，高频信号有所失真，导致图像边缘模糊；

③在反投影图不断叠加过程中，能够看到这种叠加方式会带来明显的“星状伪迹“，这是造成图像边缘模糊的最重要因素。在投影数据少的时候更明显（现实中投影数据的多少取决于机器）。

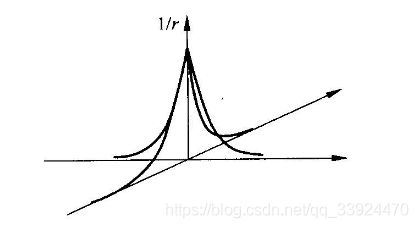
关于第③点，在数学上有研究表明，反投影重构后的图像fb(x,y)，和真实原图f(x,y)之间存在以下卷积关系：

如果要重构成真实的图像，就需要把这个由于反投影法本身带来的1/r效应去掉，由于1/r会使得图片变得模糊，因此1/r也称之为模糊因子。在实际操作中，把1/r影响去除的方法这就是下面这种最常用的（计算机、商业普遍使用）CT图像重构方法：滤波反投影法。

 

（3）滤波反投影法

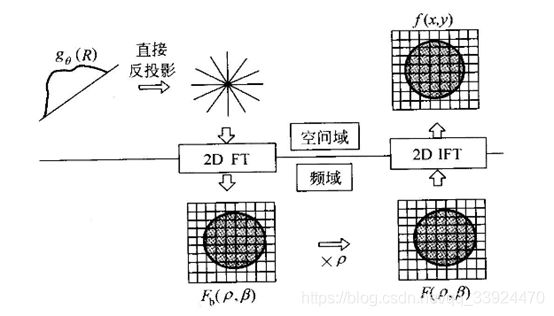
从上面的式（1）可以看到，1/r跟原图像是卷积关系，通过傅里叶变换转变到频域上后会变成乘积关系，这说明直接在频率上处理会更加简便。

在频域中，式（3）中的r称之为权重因子，其实就相当于一个滤波器，想要去除模糊因子的影响，重构成原始图像，只需要三步：

①把重构图像fb(x,y)进行二维傅里叶变换得到Fb(x,y)

②在频域中把Fb(x,y)与滤波器r相乘

③把r×Fb(x,y)进行二维傅里叶逆变换即能够得到原图f(x,y)

具体过程见下图，图中的ρ就是公式中的r。

      

图4  直接反投影法

 

这种先反投影，后滤波的方法需要用到两次二维傅里叶变换，计算量太大，因此也不是一个特别理想的矫正方法。

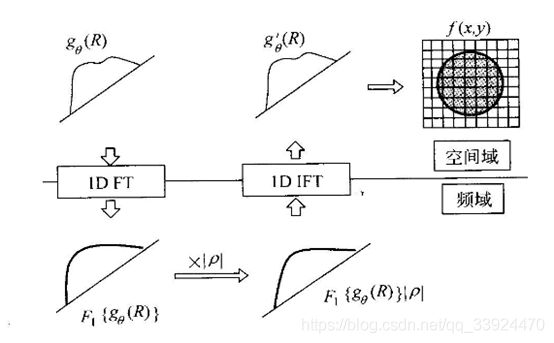
而滤波反投影法，顾名思义就是先滤波，后反投影的重构方法。具体步骤如下：

①对180个投影信号先分别进行一维傅里叶变换

②在频域中对所有投影信号进行滤波，也就是乘上权重因子r

③把所有滤波后的信号再进行一维傅里叶逆变换，还原到时域

④对每一个已经滤波的投影信号进行反投影，最后叠加（这一步跟前面的直接反投影法步骤完全相同，只是投影信号已经过了滤波）

具体流程见下图：

图5  滤波反投影法

这个方法的好处是，把两次二维傅里叶变换变成了两次一维傅里叶变换，计算速度大大提升。于是滤波反投影法的核心问题就变成了如何选择一个合适的滤波器r。数学中的滤波器r是一个理想化的滤波函数，现实中不存在，因此只能设计一个近似的滤波函数来代替r的作用。

下面常用的滤波函数有：R-L滤波函数和S-L滤波函数。

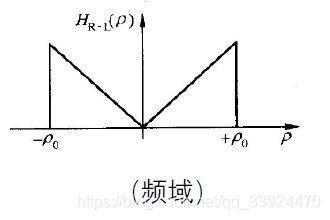
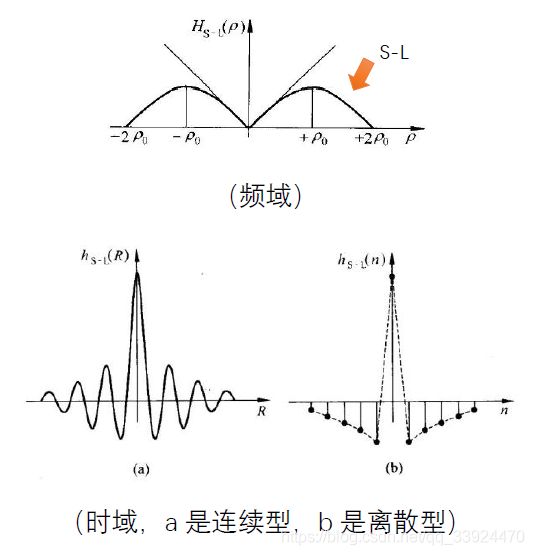
①R-L滤波函数（Ramp-Lak滤波器）

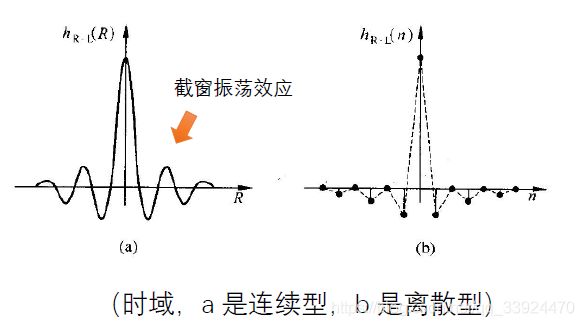
从频域图中可以看到该滤波器的作用是把低频信号减少，从而突出高频信号，因此经过该函数滤波后，重建图像的轮廓会更清晰，并且函数简单，实现起来更方便。但由于该函数在频域上有一个加窗处理（就是把高频部分直接截断了），因此在时域中会出现有许多振荡的小尾巴（截窗振荡效应），这将会让重构出来的图像存在Gibb’s现象（重构图像存在振荡，不连续）。

②S-L滤波函数（Shepp-Logan滤波器）

S-L滤波器在频域上不是直接加窗截断，而是通过一些比较平滑的窗函数对函数进行约束。因此经过S-L滤波后重构的图像振荡更少，重构的图像质量比R-L滤波器更好一些，但是因为S-L在高频段并没有直接截断，偏离了理想滤波器的效果，因此在高频段（轮廓）上的重构效果没有R-L滤波器好。

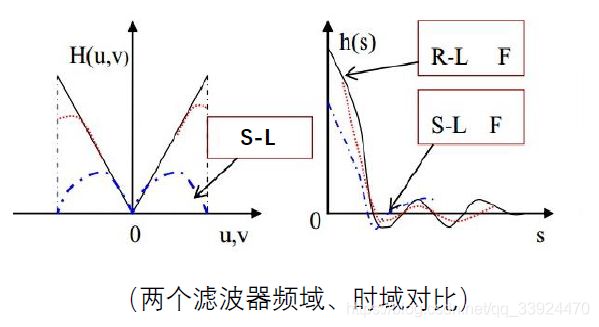
可以在下图更直观地看到两个滤波器之间的区别：

下面通过MATLAB编程来还原一下滤波反投影法的过程（程序在最后，只用复杂那个图进行展示）：

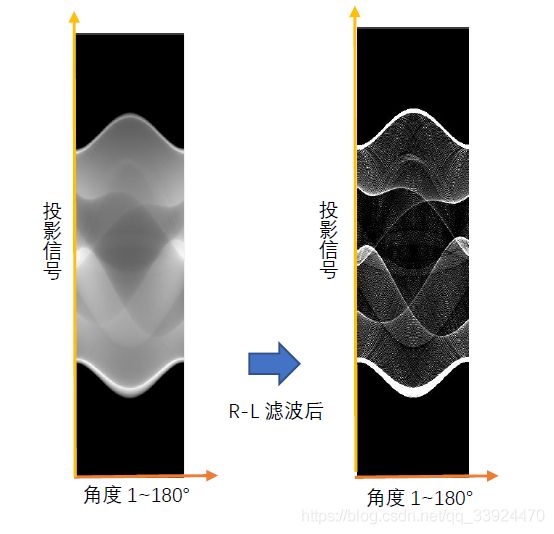
①对每一列投影信号分别在频域进行R-L滤波(高频信号明显突出了)

②对每个滤波后的投影信号反投影（这里开始与直接反投影法一样）

③ 把所有反投影图像叠加起来 

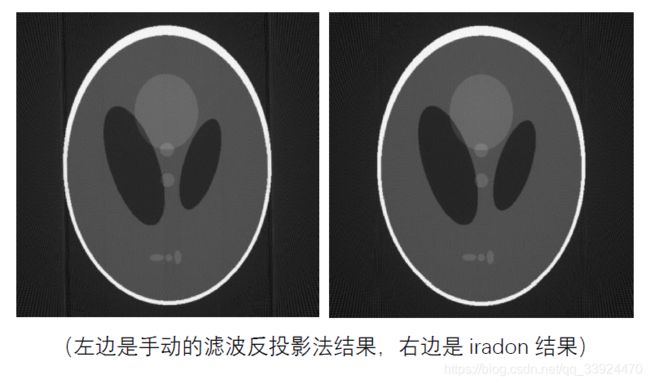
为了验证手动重构的效果，下面将使用matlab中的iradon函数直接对CT投影数据进行重构，把手动重构的图像和matlab自带函数重构的图像进行对比。

（iradon是matlab中的拉东逆变换函数，但是其实际采用的重构方法并不是对数据进行二维傅里叶逆变换，而是通过滤波反投影法实现的，且默认插值方法为“线性插值linear“，默认滤波方法为”R-L滤波函数“，这在matlab的help中可以直接看到。）

仔细观察两个重构结果，会发现iradon的重构结果更光滑一些，那是因为手动方法只是简单粗暴地把全部离散的反变换图片叠加起来，而iradon则会在最后对图像进行线性插值，使得图像更连续更光滑，重构效果更好。

最后把iradon重构的图像放大来看看图像细节：

可以看到重构的图像其实并不连续，甚至能够看出一些振荡的波纹，这就是R-L滤波函数截窗振荡效应所带来的Gibb’s现象。

 

（4）MATLAB程序

%% CT反投影法
%%==========================Part 1==========================
%% 1、直接反投影法
% 绘制一张简单的图，进行直接反投影法
clc,clear,close all
% ================================================
% 简单图
% I=zeros(512,512);
% for i=1:512
%     for j=1:512
%         if ((i-256)*(i-256)+(j-256)*(j-256))<1024
%             I(i,j)=1;
%         end
%     end
% end
% figure,imshow(I,[]);
% ===============================================

%============================================
% 复杂图
I = phantom(512); 
figure,imshow(I,[]);
%============================================

% 绘制代表角度的反投影图像
R=radon(I,0:179);  %对物体CT扫描180°的数据，每1°扫描一次
figure,imshow(R,[]);title('CT图像');
% 绘制1、45、90、135、180的投影信号和反投影图像
theta=[1 45 90 135];
for i=1:length(theta)
    r=R(:,i);
    II=iradon([r r],[theta(i) theta(i)],'linear','none')/2;%回抹（反投影）之前不滤波
    II1{i}=II;
    figure,
    subplot(1,2,1),imshow(r,[]);title([num2str(theta(i)) '°投影信号']);
    subplot(1,2,2),imshow(II,[]);title(['往' num2str(theta(i)) '°方向反投影']);
end
II2=II1{1}+II1{2}+II1{3}+II1{4};
figure,imshow(II2,[]);

% 对反投影图像进行叠加
r=R(:,1);
II_r=iradon([r r],[1 1])/2;
k=[30 15 10 1];
for j=1:4
    A=II_r;
    for i=2:k(j):180
        r=R(:,i);
        II=iradon([r r],[i i],'linear','none')/2;%回抹（反投影）之前不滤波
        A=A+II;   
    end
%     figure,imshow(A,[min(min(I)) max(max(I))]);
    figure,imshow((A),[]);
end



%% =========================Part 2=============================
%% 2、滤波反投影法
clc,clear,close all
% 复杂图
I = phantom(512); 
figure,imshow(I,[]);

% 对投影做傅里叶变换
R=radon(I,0:179);
width=length(R);
% 设计R-L滤波器
filter=2*[0:round(width/2-1), width/2:-1:1]'/width;
% 展示滤波前的CT投影信号
figure,imshow(R,[]),title('滤波前的CT投影信号');

% 每一列做傅里叶变换
r_fft=fft(R,729); 
% 每一列做傅里叶变换后滤波
r_fft_filter=r_fft.*filter; 
% 滤波后反变换(real取实部)
r_fft_filter_v=real(ifft(r_fft_filter));
% 展示滤波后的CT投影信号
% figure,imshow(r_fft_filter_v,[]),title('滤波后的CT投影信号');
figure,imshow(r_fft_filter_v),title('滤波后的CT投影信号');

% 绘制1、45、90、135、180的投影信号和反投影图像
theta=[1 45 90 135];
for i=1:length(theta)
    r=r_fft_filter_v(:,i);
    II=iradon([r r],[theta(i) theta(i)],'linear','none')/2;
    %由于iradon默认有滤波，因此关掉默认的滤波选项（none），直接用上面已经手动滤波的数据进行反投影
    II1{i}=II;
    figure,
    subplot(1,2,1),imshow(r,[]);title([num2str(theta(i)) '°投影信号']);
    subplot(1,2,2),imshow(II,[]);title(['往' num2str(theta(i)) '°方向反投影']);
end
II2=II1{1}+II1{2}+II1{3}+II1{4};
figure,imshow(II2,[]);

% 对反投影图像进行叠加
r=r_fft_filter_v(:,1);
II_r=iradon([r r],[1 1])/2;
k=[30 15 10 1];
for j=1:4
    A=II_r;
    for i=2:k(j):180
        r=r_fft_filter_v(:,i);
        II=iradon([r r],[i i],'linear','none')/2;
        %由于iradon默认有滤波，因此关掉默认的滤波选项（none），直接用上面已经手动滤波的数据进行反投影
        A=A+II;   
    end
%     figure,imshow(A,[min(min(I)) max(max(I))]);
    figure,imshow((A),[]);
end

% 上面是反投影叠加的分步计算，下面直接输入全部投影数据到iradon函数中进行验证
B=iradon(r_fft_filter_v,0:179,'linear','none');
figure,
imshow(B,[]);title('验证：滤波后图像');

 

---

以上就是对CT图像重构的整理结果，更多是自己在学习过程中的理解，若有表述不当的地方欢迎指出。