概率图模型（1）：CRF(conditional random field)线性条件随机场

概率图模型的综合叙述：

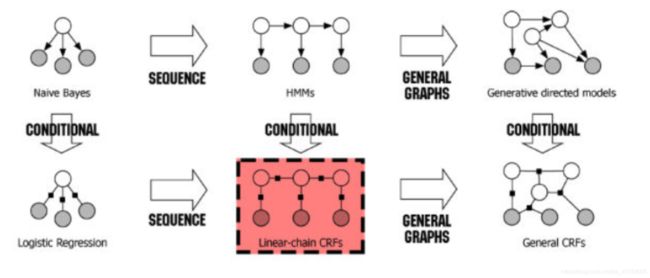
特征函数便是图中的conditional。对图简单的说明，综合概述Naive Bayes，Logistic Regression，HMM，Linear-chain CRF之间的关系。Naive Bayes经过条件参数的加入即为Logistic Regression，同时这两者经过序列化即特征函数加入了对相邻状态之间的判断即变为HMM和Linear-chain CRF，最后经过广义图模型的扩展变为最后两者。

CRF 综述

CRF(conditional random field)简单而又直白的讲，线性条件随机场，是只考虑概率图中相邻变量是否满足特征函数$F(y,x)$的一个模型。

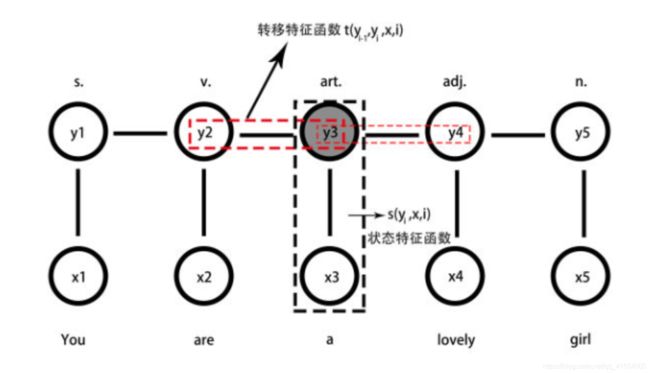
下面看一个词性标注任务的例子：

定义转移特征函数：$t(y_2=v.,y_3=v.,x,i)=-1$（两个动词相连我们可以给负分）（y2y3都是动词的时候扣分）

定义状态特征函数：$s\left(y_3=ar{t}_{\cdot },x,i\right)=1$（把 a 标注成不定冠词可以给正分）（y3是不定冠词的时候加分）

条件随机场的参数化定义为：
$$\begin{array}{l}P(y|x)=\frac{1}{Z(x)}\exp \left({\sum }_{i,k}{\lambda }_k{t}_k\left(y_{i-1},y_i,x,i\right)+{\sum }_{i,l}{\mu }_l{s}_l\left(y_i,x,i\right)\right)\\ Z(x)={\sum }_y\exp \left({\sum }_{i,k}{\lambda }_k{t}_k\left(y_{i-1},y_i,x,i\right)+{\sum }_{i,l}{\mu }_l{s}_l\left(y_i,x,i\right)\right)\end{array}$$
每一项的含义：

${\sum }_{i,k}{\lambda }_k{t}_k\left(y_{i-1},y_i,x,i\right)$共计$k$个转移特征函数条件下每一个函数针对不同的输入位置$i$给出的评分总和。

${\sum }_{i,l}{\mu }_l{s}_l\left(y_i,x,i\right))$共计$l$个状态特征函数条件下每一个函数针对不同的输入位置$i$给出的评分总和。

简化表达

当我们给每个特征函数（转移特征和状态特征）不同的权重$w$（转移特征的权重 ${\lambda }_k$与状态特征的权重${\mu }_l$统一用$w$表示)，把转移特征$t\left(y_{i-1},y_i,x,i\right)$和状态特征$s\left(y_i,x,i\right)$同一写成$F(y,x)$后：

$P_w(y|x)=\frac{1}{Z_W(x)}\exp (w\cdot F(y,x))$
$Z_w(x)={\sum }_y\exp (w\cdot F(y,x))$

理解：

满足特征条件越多越容易出现更高的概率，条件随机场模型在统计语料库中相邻词是否满足特征函数的频数，并依此给出$P_w(y|x)$。在给定的$(x,y)$，满足的特征函数越多，模型$P_w(y|x)$认为越大。