1.算法思想
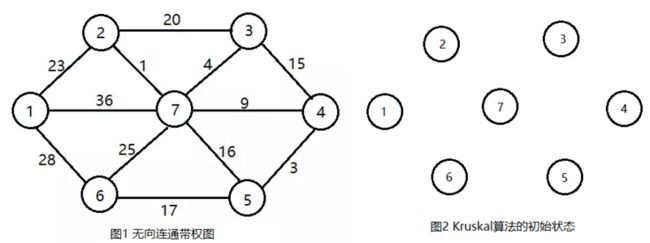
- 构造最小生成树除了Prim算法,还有Kruskal算法。设G=(V,E)是无向连通带权图,设最小生成树T=(V, TE), TE表示已经加入最小生成树的边的集合。
- Kruskal算法思想是:Kruskal算法将带权无向图中的n个节点看成是n个独立的连通分支。它首先将所有的边按权值从小到大排序,然后只要选中的边数不到n-1,就做如下贪婪选择:在边集E中选出权值最小的边(i, j),如果将边(i, j)加入集合TE中不产生回路,则将边(i, j)加入集合边集TE中,即用边(i, j)将这两个连通分支合并连接成一个连通分支;如果加入边(i, j)后出现了回路,将把边(i, j)从集合E中删去。继续上面的贪心选择,直到T中所有顶点都在同一个连通分支上为止。此时,选取到的n-1条边恰好构成G的一棵最小生成树T。
- 然而,如何判断加入某条边后最小生成树T会不会出现回路呢?
- Kruskal算法引入了连通分量来判断,简单地说,最小生成树在生成的过程中,已经加入到结合TE中的边和顶点属于一个连通分量,没加入的边和顶点属于其它连通分量,当新的一条边加入时,判断它的两个顶点是否属于一个连通分量,如果都是一个连通分量,则必然会成环,如下图所示,继续选择下一个权值最小的边,如果两个节点属于不同连通分量,则将这条边加入TE中。
2.算法设计
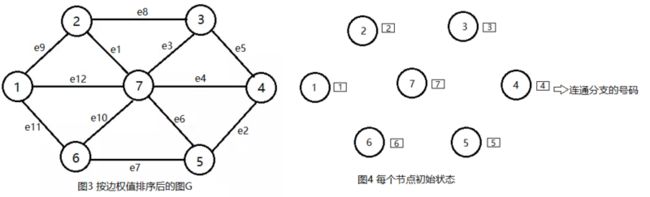
- 步骤1:初始化。将图G的边集E中的所有边按权值从小到大排序,边集TE = { },把每个顶点都初始化为一个孤立的连通分支,即一个顶点对应一个连通分量(支);
- 步骤2:在E中寻找权值最小的边(i, j);
- 步骤3:如果顶点i和j位于两个不同的连通分支,则将边(i, j)加入边集TE,并执行合并操作,将两个连通分支进行合并;
- 步骤4:将边(i,j)从所有边的集合E中删去,即E = E - {(i, j)};
- 步骤5:如果选取边数小于n-1,转步骤2;否则,算法结束,生成最小生成树T。
3.算法图解
(1) 初始化
将图G的边集E中的所有边按权值从小到大排序,初始化节点状态,一个节点对应一个连通分支,如下图所示,同时初始化最小生成树TE = {}。
(2) 找最小
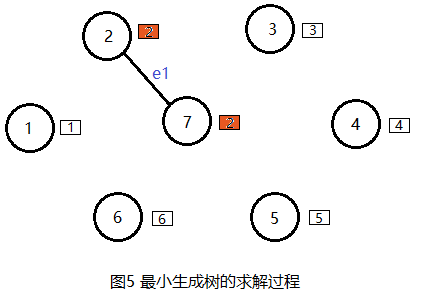
在边集E中选择最小的边e1(2, 7), 权值为1。
(3) 合并
节点2和节点7属于两个不同的连通分支,因此可以将边(2, 7)加入边集TE,执行合并操作后将两个连通分支合并成一个连通分支,同时我们规定连通分支号码小的取代连通分支号码大的,如下图所示。
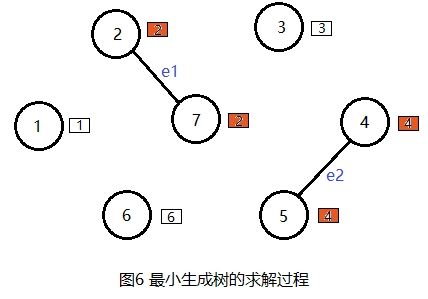
(4) 找最小
在边集E中选择最小的边e2(4,5), 权值为3。
(5) 合并
(6) 找最小
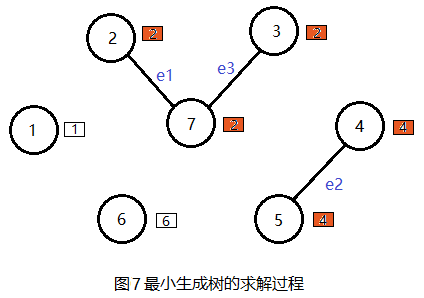
在边集E中选择最小的边e3(3,7), 权值为4。
(7) 合并
(8) 找最小
在边集E中选择最小的边e4(4,7), 权值为9。
(9) 合并
(10) 找最小
在边集E中选择最小的边e5(3,4), 权值为15。
(11) 合并
节点3和节点4属于一个连通分支,会产生回路,舍弃。
(12) 找最小
在边集E中选择最小的边e6(5,7), 权值为16。
(13) 合并
节点5和节点7属于一个连通分支,会产生回路,舍弃。
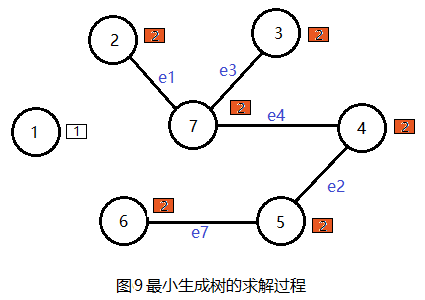
(14) 找最小
在边集E中选择最小的边e7(5,6), 权值为17。
(15) 合并
(16) 找最小
在边集E中选择最小的边e8(2,3), 权值为20。
(17) 合并
节点2和节点3属于一个连通分支,会产生回路,舍弃。
(18) 找最小
在边集E中选择最小的边e8(1,2), 权值为23。
(19) 合并
(20) 算法结束,TE选中的边即为最小生成树。
4.代码片段展示
(1) 数据结构
// 数据结构
struct Edge {
int start; // 起点
int end; // 终点
int weight; // 权值
// 自定义排序规则
bool operator < (const Edge& edge) {
return weight < edge.weight;
}
};(2) 初始化
// 初始化
vector Init(int m) {
vector edges(m);
cout << "请依次输入" << m << "条边的起点,终点和权值(用空格隔开):" << endl;
for (int i = 0; i < m; i++) {
cin >> edges[i].start >> edges[i].end >> edges[i].weight;
}
return edges;
} (3) 合并连通分支
// 合并操作
int Merge(vector& nodeSet, Edge& edge) {
int n = nodeSet.size() - 1;
// 分别表示边的起点和终点的连通分支的编号
int p = nodeSet[edge.start];
int q = nodeSet[edge.end];
// 如果两个边的起点和终点在一个连通分支中,直接舍弃,不做处理
if (p == q) return 0;
for (int i = 1; i <= n; i++) {
if (nodeSet[i] == q) {
// 编号为q的连通分支下的所有节点都合并在连通分支p中
nodeSet[i] = p;
}
}
return 1;
} 5.代码实现
// Kruskal实现最小生成树
#include
#include
#include
using namespace std;
const int N = 100;
// 数据结构
struct Edge {
int start; // 起点
int end; // 终点
int weight; // 权值
bool operator < (const Edge& edge) {
return weight < edge.weight;
}
};
// 初始化
vector Init(int m) {
vector edges(m);
cout << "请依次输入" << m << "条边的起点,终点和权值(用空格隔开):" << endl;
for (int i = 0; i < m; i++) {
cin >> edges[i].start >> edges[i].end >> edges[i].weight;
}
return edges;
}
// 合并操作
int Merge(vector& nodeSet, Edge& edge) {
int n = nodeSet.size() - 1;
// 分别表示边的起点和终点的连通分支的编号
int p = nodeSet[edge.start];
int q = nodeSet[edge.end];
// 如果两个边的起点和终点在一个连通分支中,直接舍弃,不做处理
if (p == q) return 0;
for (int i = 1; i <= n; i++) {
if (nodeSet[i] == q) {
// 编号为q的连通分支下的所有节点都合并在连通分支p中
nodeSet[i] = p;
}
}
return 1;
}
// 返回最小生成树中选中的边
vector Kruskal(vector& edges, int n) {
// nodeSet保存连通分支的编号
vector nodeSet(n + 1);
for (int i = 1; i <= n; i++) {
nodeSet[i] = i;
}
sort(edges.begin(), edges.end());
int m = edges.size();
// 保存最小生成树中选中的边
vector tree;
// 选最小并合并
for (int i = 0; i < m; i++) {
if (Merge(nodeSet, edges[i])) {
tree.push_back(edges[i]);
n--;
// 只要找到n-1条有效边选路就算完成
if (n == 1) return tree;
}
}
return tree;
}
void PrintTree(vector& tree) {
cout << "\n最小生成树中选中的边如下:" << endl;
int cost = 0;
for (const auto& edge : tree) {
cout << "\t" << edge.start << "<-->" << edge.end << " 权值:" << edge.weight << endl;
cost += edge.weight;
}
cout << "\n最小生成树的总权值为:" << cost << endl;
}
int main() {
int n, m; // n为节点数量,m为边的数量
cout << "请依次输入无向图节点数量和边的数量(用空格隔开):" << endl;
cin >> n >> m;
vector edges = std::move(Init(m));
vector tree = Kruskal(edges, n);
PrintTree(tree);
return 0;
} 6.实验结果
请依次输入无向图节点数量和边的数量(用空格隔开):
7 12
请依次输入12条边的起点,终点和权值(用空格隔开):
1 2 23
1 6 28
1 7 36
2 3 20
2 7 1
3 4 15
3 7 4
4 5 3
4 7 9
5 6 17
5 7 16
6 7 25
最小生成树中选中的边如下:
2<-->7 权值:1
4<-->5 权值:3
3<-->7 权值:4
4<-->7 权值:9
5<-->6 权值:17
1<-->2 权值:23
最小生成树的总权值为:57
E:\codeDir\algorithms\x64\Debug\algorithms.exe (进程 8232)已退出,返回代码为: 0。7.算法优化
显然,贪心法实现的Kruskal算法的时间复杂度是O(n^2),在合并两个连通分支的时候,我们可以用并查集的思想,直接将两个连通分支的根连在一起,这样合并操作时间复杂度将为O(logn),总体时间复杂度降为O(nlogn)。
8.代码实现(优化后)
// 运用并查集优化Kruskal实现最小生成树
#include
#include
#include
using namespace std;
const int N = 100;
// 数据结构
struct Edge {
int start; // 起点
int end; // 终点
int weight; // 权值
bool operator < (const Edge& edge) {
return weight < edge.weight;
}
};
// 找到节点r在连通分支中的根(新加!!!)
int FindRoot(vector& nodeSet, int r) {
int root = r;
while (nodeSet[root] != -1) {
root = nodeSet[root];
}
return root;
}
// 初始化
vector Init(int m) {
vector edges(m);
cout << "请依次输入" << m << "条边的起点,终点和权值(用空格隔开):" << endl;
for (int i = 0; i < m; i++) {
cin >> edges[i].start >> edges[i].end >> edges[i].weight;
}
return edges;
}
// 合并操作(修改!!!)
int Merge(vector& nodeSet, Edge& edge) {
int n = nodeSet.size() - 1;
// 分别表示边的起点和终点的连通分支的编号
int p = FindRoot(nodeSet, edge.start);
int q = FindRoot(nodeSet, edge.end);
// 如果两个边的起点和终点在一个连通分支中,直接舍弃,不做处理
if (p == q) return 0;
// 将连通连通分支的根相连
else nodeSet[q] = p;
return 1;
}
// 返回最小生成树中选中的边
vector Kruskal(vector& edges, int n) {
// nodeSet保存连通分支的编号,全部初始化为-1, 表示连通分支的根(修改!!!)
vector nodeSet(n + 1);
for (int i = 1; i <= n; i++) {
nodeSet[i] = -1;
}
sort(edges.begin(), edges.end());
int m = edges.size();
// 保存最小生成树中选中的边
vector tree;
// 选最小并合并
for (int i = 0; i < m; i++) {
if (Merge(nodeSet, edges[i])) {
tree.push_back(edges[i]);
n--;
// 只要找到n-1条有效边选路就算完成
if (n == 1) return tree;
}
}
return tree;
}
void PrintTree(vector& tree) {
cout << "\n最小生成树中选中的边如下:" << endl;
int cost = 0;
for (const auto& edge : tree) {
cout << "\t" << edge.start << "<-->" << edge.end << " 权值:" << edge.weight << endl;
cost += edge.weight;
}
cout << "\n最小生成树的总权值为:" << cost << endl;
}
int main() {
int n, m; // n为节点数量,m为边的数量
cout << "请依次输入无向图节点数量和边的数量(用空格隔开):" << endl;
cin >> n >> m;
vector edges = std::move(Init(m));
vector tree = Kruskal(edges, n);
PrintTree(tree);
return 0;
} 8.实验结构(优化后)
请依次输入无向图节点数量和边的数量(用空格隔开):
7 12
请依次输入12条边的起点,终点和权值(用空格隔开):
1 2 23
1 6 28
1 7 36
2 3 20
2 7 1
3 4 15
3 7 4
4 5 3
4 7 9
5 6 17
5 7 16
6 7 25
最小生成树中选中的边如下:
2<-->7 权值:1
4<-->5 权值:3
3<-->7 权值:4
4<-->7 权值:9
5<-->6 权值:17
1<-->2 权值:23
最小生成树的总权值为:57贪心算法这段旅程到这里就圆满结束了,我们下期分治算法再会~~~
我是lioney,年轻的后端攻城狮一枚,爱钻研,爱技术,爱分享。
个人笔记,整理不易,感谢阅读、点赞和收藏。
文章有任何问题欢迎大家指出,也欢迎大家一起交流后端各种问题!