Tensorflow卷积中Padding的两种方式
Tensorflow卷积中Padding的两种方式
两种Padding
- VALID:若不够滑动,则将右下的剩余部分全部舍弃,从原矩阵左上角开始卷积。
H ′ = ⌈ H − k + 1 d ⌉ H'=\left \lceil \frac{H-k+1}{d} \right \rceil H′=⌈dH−k+1⌉
- SAME:如果 H / d H/d H/d除不尽,会均匀地在左上、右下补0,令总长 L L L满足 L − k + 1 = d H L-k+1=dH L−k+1=dH,若补不够,则往右下补。
H ′ = ⌈ H d ⌉ H'=\left \lceil \frac{H}{d} \right \rceil H′=⌈dH⌉
H H H表示卷积前尺寸, H ′ H' H′表示卷积后尺寸, k k k为卷积核尺寸, d d d为步长, ⌈ x ⌉ \left \lceil x \right \rceil ⌈x⌉表示向上取整。
在 Tensorflow 的 nn_ops.py 中有关于卷积运算输出尺寸的定义。
If padding == "SAME":
output_spatial_shape[i] = ceil(input_spatial_shape[i] / strides[i])
If padding == "VALID":
output_spatial_shape[i] =
ceil((input_spatial_shape[i] -
(spatial_filter_shape[i]-1) * dilation_rate[i])
/ strides[i]).
举例
例一
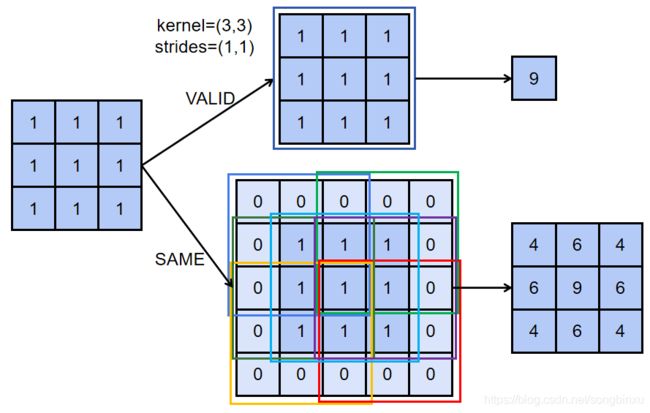
考虑大小为 ( N , 3 , 3 , C ) (N,3,3,C) (N,3,3,C)的输入,忽略 b a t c h s i z e batchsize batchsize 和 c h a n n e l channel channel,即考虑 ( 3 , 3 ) (3,3) (3,3) 大小的矩阵。现在用 ( 3 , 3 ) (3,3) (3,3) 大小的卷积核(方便起见,卷积核参数均为1)做步长 ( 1 , 1 ) (1,1) (1,1) 的卷积。padding=VALID 时,直接从矩阵左上角开始滑动,刚好 ( 3 , 3 ) (3,3) (3,3) 覆盖到了矩阵右下角,卷积结束,padding=SAME 时,先在周围补零,需要补零至长度 L L L,使 L − k + 1 = d H L-k+1=dH L−k+1=dH,故此处应补至5,即左上和右下各补一圈即可。最后再从补零后的矩阵的左上角开始滑动,直到右下角。
例二
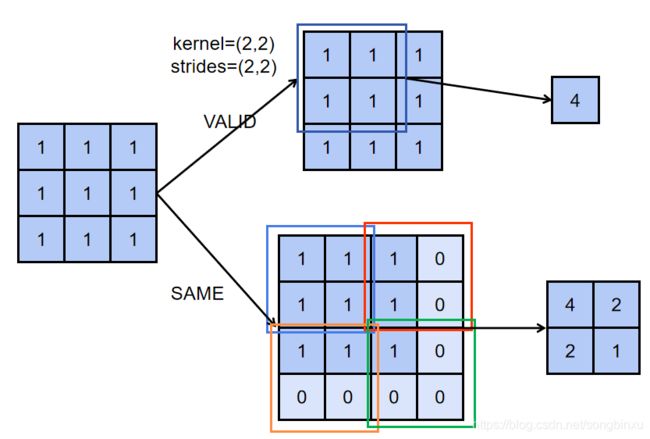
考虑大小为 ( N , 3 , 3 , C ) (N,3,3,C) (N,3,3,C)的输入,忽略 b a t c h s i z e batchsize batchsize 和 c h a n n e l channel channel,即考虑 ( 3 , 3 ) (3,3) (3,3) 大小的矩阵。现在用 ( 2 , 2 ) (2,2) (2,2) 大小的卷积核(方便起见,卷积核参数均为1)做步长 ( 2 , 2 ) (2,2) (2,2) 的卷积。padding=VALID 时,直接从矩阵左上角开始滑动, ( 2 , 2 ) (2,2) (2,2) 没有到达矩阵右下角,卷积就结束了,剩余的将直接舍弃掉。padding=SAME 时,先在周围补零,这里需要补长至4,优先补右下角,故在右下补一圈0。最后再从补零后的矩阵的左上角开始滑动,直到右下角。
参考
Tensorflow中padding的两种类型SAME和VALID
Tensorflow卷积与反卷积(目前看到的最详细的解释)
TensorFlow中CNN的两种padding方式“SAME”和“VALID”
tf.nn.conv2d_transpose
Tensorflow nn_ops.py