第六章 堆排序习题
6.1堆
堆节点的高度:为该节点到叶节点最长简单路径上#边的个数#。(因此,根节点所在位置高度为0)
6.1-1 在高度为h的堆中,元素个数最多和最少分别是多少?
6.1-2 证明:含n个元素的堆的高度为 ⌊lgn⌋ 。
证明:1)利用上面式子反推
2)数学归纳法证明即可
6.1-3 证明:在最大堆的任一子树中,该子树所包含的最大元素在该子树的根结点上。
最大堆的性质是指除了根节点以外的所有节点i都要满足:A[PARENT(i)]>=A[i]
而根节点又是所有节点的祖先节点,故最大元素必然在该子树的根节点上。
6.1-4 假设一个最大堆的所有元素都不相同,那么该堆的最小元素应该位于哪里?
某个叶子节点上,但不确定是哪一个叶子节点。
6.1-5 一个已排好的数组是一个最小堆吗?
是
6.1-6 值为<23,17,14,6,13,10,1,5,7,12>的数组是一个最大堆吗?
不是,因为7是6的孩子节点,并且比6大。
6.1-7 证明:当用数组表示存储n个元素的堆时,叶节点下标分别是 ⌊n2⌋+1,⌊n2⌋+2,…,n 。
下式中n的下标表示孩子个数的节点,其中拥有一个孩子的节点最多只能有一个,这是由堆的性质决定的;而叶子节点有0个孩子节点,且必然排在最后。
6.2维护堆的性质
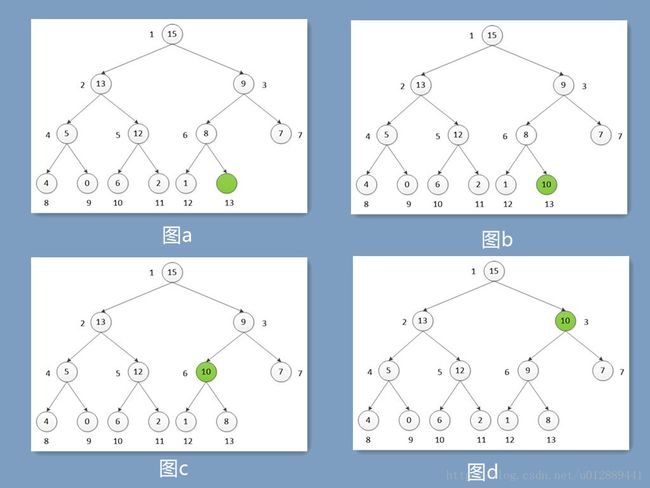
6.2-1 参照图6-2的方法,说明MAX-HEAPIFY(A,3)在数组A=<27,17,3,16,13,10,1,5,7,12,4,8,9,0>上的操作过程。
当A.heap-size=14时,MAX-HEAPIFY(A,3)的执行过程。a)初始状态,在节点i=3处,A[3]违背了最大堆性质,因为它的值不大于它的孩子。在b)中,通过交换A[3]和A[6]的值,节点3恢复了最大堆的性质,但又导致了节点6违反了最大堆的性质。递归调用MAX-HEAPIFY(A,6),此时i=6。在c)中,通过交换A[6]和A[13]的值,节点6的最大堆的性质得到了恢复。再次递归调用MAX-HEAPIFY(A,13),此时不再有新的数据交换。
6.2-2 参考过程 MAX-HEAPIFY,写出能够维护相应最小堆的MIN-HEAPIFY(A,i)的伪代码,并比较MIN-HEAPIFY与MAX-HEAPIFY的运行时间。
MAX-HEAPIFY(A,i)
i= LEFT(i)
r= RIGHT(i)
if l <= A.heap-size and A[l]<A[i]
smallest=l
else
smallest=i
if r <= A.heap-size and A[r]<A[smallest]
smallest=r
if smallest!=i
exchange A[i] with A[smallest]
MAX-HEAPIFY(A,smallest)运行时间相同
6.2-3 当元素A[i]比其孩子的值都大时,调用MAX-HEAPIFY(A,i)会有什么结果。
一次运行完毕,不会递归。
6.2-4 当 i>A.heap-size/2 时,调用 MAX-HEAPIFY(A,i)会有什么结果?
说明i是叶子节点,也会直接结束,不会递归。
6.2-5 MAX-HEAPIFY的代码效率较高,但第10行中的递归调用可能例外,它可能使某些编译器产生低效的代码。请用循环去掉递归,重写 MAX-HEAPIFY代码。
MAX-HEAPIFY(A,i)
while(1)
{
i= LEFT(i)
r= RIGHT(i)
if l <= A.heap-size and A[l]>A[i]
largest=l
else
largest=i
if r <= A.heap-size and A[r]>A[largest]
largest=r
if largest!=i
exchange A[i] with A[largest]
else
return
i=largest
}6.2-6 证明:对一个大小为n的堆,MAX-HEAPIFY的最坏情况运行时间为Ω(lgn)。(提示:对于n个节点的对,可以通过对每个几点设定恰当的值,使得从根节点到叶节点路径上的每个节点都会递归调用MAX-HEAPIFY.)
正如提示里所说,那么最坏的运行时间就是,树的深度。
6.3建堆
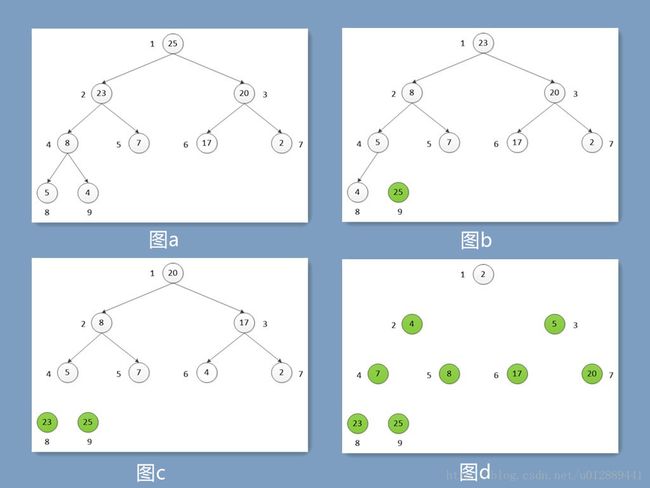
6.3-1 参照图6-3的方法,说明BUILD-MAX-HEAP在数组A=<5,3,17,10,84,19,6,22,9>上的操作过程。

BUILD-MAX-HEAP的操作过程示意图,显示了在BUILD-MAX-HEAP的第三行调用MAX-HEAPIFY之前的数据结构。a)一个包括9个元素的二叉树。图中显示的是调用MAX-HEAPIFY(A,i)前,循环控制变量i指向结点4的情况。b)操作结果的数据结构。下一次迭代,循环控制变量i节点指向3.c)、d)BUILD-MAX-HEAP中执行for循环的后续迭代操作。需要注意的是,任何时候在某个节点调用MAX-HEAPIFY,该节点的两个子树都是最大堆。e)执行完BUILD-MAX-HEAP时的最大堆。
6.3-2 对于BUILD-MAX-HEAP中第2行的循环控制变量i来说,为什么我们要求它是从 ⌊A.length⌋到1递减,而不是从1到⌊A.length⌋ 递增呢?
因为要保证:任何时候在某个节点调用MAX-HEAPIFY,该节点的两个子树都是最大堆。这个条件。
6.3-3 证明:对于任一包含n个元素的堆中,至多有 ⌈n/2h+1⌉ 个高度为h的节点。
6.4堆排序算法
6.4-1 参照6-4的方法,说明HEAPSORT在数组A=<5,13,2,25,7,17,20,8,4>上的操作过程。
6.4-2 试分析在使用下列循环不变量时,HEAPSORT的正确性:
在算法的第2~5行for循环每次迭代开始时,子数组A[1…i]是一个包含了数组A[1……n]中第i小元素的最大堆,而子数组A[i+1…n]包含了数组A[1…n]中已排序的n-i个最大元素?
i+1…n是取了n-i次最大堆顶部的结果,每次最大堆顶部的值一定是整个堆中最大的,所以子数组A[i+1…n]包含了数组已排序的n-i个最大元素,而剩下的元素一定比这些元素都小,所以包含了第i小元素。
6.4-3 对于一个按升序排列的包含n个元素的有序数组A来说,HEAPSORT的时间复杂度是多少?如果A是降序呢?
升序,最坏情况O(nlgn)
降序,不用进行第一次排序,θ(lg(n!))
6.4-4 证明:在最坏情况下,HEAPSORT的时间复杂度是Ω(nlgn)。
故时间富足度为nlgn
6.5 优先队列
6.5-1 试说明HEAP-EXTRACT-MAX在堆A=<15,13,9,5,12,8,7,4,0,6,2,1>上的操作过程。
6.5-2 试说明MAX-HEAP-INSERT(A,10)在堆A=<15,13,9,5,12,8,7,4,0,6,2,1>上的操作过程。
6.5-3 要求用最小堆实现最小优先队列,请写出HEAP-MINIMUM、HEAP-EXTRACT-MIN、HEAP-DECREASE-KEY和MIN-HEAP-INSERT的伪代码。
HEAP-MINIMUM
return A[1]
HEAP-EXTRACT-MIN
if A.heap-size<1
error "heap underflow"
min=A[1]
A[1]=A[A.heap-size]
A.heap-size=A.heap-size-1
MIN_HEAPIFY(A,1)
return min
HEAP-DECREASE-KEY
if key>A[i]
error "new key is larger than current key"
A[i]=key
while i>1 and A[PARENT(i)]>A[i]
exchange A[i] with A[PARENT(i)]
i=PARENT(i)
MIN-HEAP-INSERT
A.heap-size=A.heap-size+1
A[A.heap-size]=+∞
HEAP-DECREASE-KEY(A,A.heap-size,key)6.5-4 在MAX-HEAP-INSERT的第2行,为什么我们要先把关键字设为-∞,然后又将其增加到所需的值呢?
依然保持大顶堆的性质。
6.5-5 试分析在使用下列循环不变量时,HEAP-INCREASE-KEY的正确性:
在算法的第4~6行while循环每次迭代开始的时候,子数组A[1…A.heap-size]要满足最大堆的性质。如果有违背,只有一个可能:A[i]大于A[PARENT(i)]。
这里,你可以假定在调用HEAP-INCREASE-KEY时,A[1…A.heap-size]是满足最大堆性质的。
初始化:调用HEAP-INCREASE-KEY时,A[1…A.heap-size]满足最大堆性质。
保持:若加入节点所在位置A[i]< A[PARENT(i)],那么加入节点并不需要调换,而其他节点也处于平衡状态。
终止:大顶堆并没改变。
所以如果有违背只有一个可能A[i] > A[PARENT(i)]
6.5-6 在HEAP-INCREASE-KEY的第5行的交换操作中,一般需要通过三次赋值来完成。想一想如何利用INSERTION-SORT内循环部分的思想,只用一次赋值就完成这一交换操作?
exchange A[i] with A[PARENT(i)]
while i>1 and A[PARENT(i)]A[i]=A[PARENT(i)]
i=PARENT(i)
A[i]=key 6.5-7 试说明如何使用优先队列来实现一个先进先出队列,以及如何使用优先队列来实现栈。
栈:每次加入叶子节点,每次取叶子节点
队列:每次加入叶子节点,每次取根节点
6.5-8 在HEAP-DELETE(A,i)操作能够将结点i从堆A中删除。对于一个包含n个元素的堆,请设计一个能够在O(lgn)时间内完成的HEAP-DELETE操作。
HEAP-DELETE(A,i)
if i>n/2
A[i+1~n]向前挪一位
return
left=LEFT(A,i)
right=RIGHT(A,i)
if(A[left]>A[right])
A[i]=A[left]
HEAP-DELETE(A,left)
else
A[i]=A[right]
HEAP-DELETE(A,right)6.5-9 请设计一个时间复杂度为O(nlgk)的算法,它能够将k个有序链表合并为一个有序链表,这里n是所有输入链表包含的总的个数。(提示:使用最小堆来完成k路归并)
思路:
1.取k个链表的第一个元素,构成一个最小堆。
2.取掉最小堆的根元素,放入result数组,若取出元素所在链表不为空,在其所在链表取出一个元素继续维持平衡。
3、若取出元素所在链表为空,堆的数量减1。
3.重复步骤2~3,直到所有链为空。
stdafx.h中
#define N 3 //规定链表的内容
#define col 8 //每个链表中的元素个数StructChain.h中
struct Chain
{
int number;
Chain * next;
};
class StructChain
{
public:
StructChain();
~StructChain();
Chain* CreateChain(int *arr,int length);
void print(Chain * head);
};StructChain.cpp中
Chain* StructChain::CreateChain(int *arr,int length)
{
//根据传入的数组创建一个有头节点的数组
Chain*head = (struct Chain *)malloc(sizeof(struct Chain));
Chain *h;
h=head;
for (int i = 0; i < length; i++)
{
Chain* p = (struct Chain *)malloc(sizeof(struct Chain));
p->number = arr[i];
h->next = p;
h = p;
}
h->next = NULL;
return head;
}
//输出链表
void StructChain::print(Chain* head)
{
Chain *p = head->next;
while (p!=NULL)
{
printf("%d\t", p->number);
p = p->next;
}
}Heap.h中
struct HeapNode
{
int number;
int fromChain;
};
class Heap
{
public:
Heap();
~Heap();
void CreateHeap(Chain *head[]);//创建一个堆
int * GetResult(Chain *head[]);//得到链表合并的结果
void CreateSmallHeap(int n);//构建小顶堆
void Exchange(int i, int j);//调换两个节点
int GetNode(Chain *head[]);//得到一个节点,并让堆继续保持平衡
void MinHeapify(int i); //重新归为最小堆
void AddHeapify(int i); //加入一个节点维持大顶堆的平衡
int n; //堆节点的大小
HeapNode Node[N]; //建立与链表数目相同的节点
int result[N*col];
};Heap.cpp中
//构建初始堆;
void Heap::CreateHeap(Chain *head[])
{
n = N;
for (int i = 0; i < N; i++)
{
Node[i].number = head[i]->next->number;
head[i]->next = head[i]->next->next;
Node[i].fromChain = i;
}
}
int * Heap::GetResult(Chain * head[])
{
//构建堆
CreateHeap(head);
//构建小顶堆
CreateSmallHeap(N);
//构造结果集
for (int i = 0; i < N*col; i++)
{
result[i] = GetNode(head);
}
return result;
}
void Heap::CreateSmallHeap(int n)
{
int pNodeNumber = n / 2;
for (int i = (N/2-1); i >=0; i--)
{
if ((i + 1) * 2 - 11) * 2 - 1].number < Node[i].number)//左侧子节点与父节点比较
{
Exchange((i + 1) * 2 - 1, i);
}
if ( (i + 1) * 21) * 2].number.number)//右侧子节点与父节点比较
{
Exchange((i + 1) * 2, i);
}
}
}
//调换两个节点的位置
void Heap::Exchange(int i, int j)
{
HeapNode tmp;
tmp = Node[i];
Node[i] = Node[j];
Node[j] = tmp;
}
int Heap::GetNode(Chain * head[])
{
HeapNode tmp = Node[0];
//重新达到小顶堆的平衡状态
Node[0] = Node[n - 1];
MinHeapify(0);
//将堆中放入新值
if (head[tmp.fromChain]->next != NULL)
{
Node[n - 1].number = head[tmp.fromChain]->next->number;
head[tmp.fromChain]->next = head[tmp.fromChain]->next->next;
Node[n-1].fromChain = tmp.fromChain;
//继续维持小顶堆的平衡
AddHeapify(n - 1);
}
else
{
n=n-1;
}
return tmp.number;
}
void Heap::MinHeapify(int i)
{
if ((i + 1) * 2 - 1<(N-1) && Node[(i + 1) * 2 - 1].number < Node[i].number)//左侧子节点与父节点比较
{
Exchange((i + 1) * 2 - 1, i);
MinHeapify((i + 1) * 2 - 1);
}
if ((i + 1) * 2<(N-1) &&Node[(i + 1) * 2].number.number)//右侧子节点与父节点比较
{
Exchange((i + 1) * 2, i);
MinHeapify((i + 1) * 2);
}
}
void Heap::AddHeapify(int i )
{
for (; i >= 0; i--)
{
if ((i + 1) / 2 - 1 >= 0 && Node[(i + 1) / 2 - 1].number> Node[i].number)
{
Exchange((i + 1) / 2 - 1, i);
i = (i + 1) / 2 - 1;
}
else
{
break;
}
}
}
main函数
int main()
{
//规定给定的N个链表
int a[][col] = { {1,3,5,7,9,11,13,17} ,{1,2,3,4,5,6,7,8},{2,4,6,8,10,12,14,16} };
StructChain chain;
//构造链表
Chain *head[N];
for (int i = 0; i < N; i++)
{
head[i] = chain.CreateChain(a[i], sizeof(a[0]) / sizeof(a[0][0]));
}
int *result;
//传入head的值,构建最小堆
Heap heap;
result = heap.GetResult(head);
for (int i=0; i < N*col; i++)
{
printf("%d\t", result[i]);
}
return 0;
}