非极大值抑制算法NMS
非极大值抑制(Non-Maximum Suppression, NMS)是目标检测任务中一个重要的后处理步骤,只要是Anchor-based的检测方法,都需要经过NMS进行后处理。一个图片经过目标检测之后,会得到大量重复的anchor,而NMS就是去除掉这些重复的anchor。
如下图所示,左边是NMS处理之前,右边表示NMS处理后。
NMS主要有两种处理方式,分别为Hard NMS和Soft NMS,下面分布介绍。
Hard NMS
Hard NMS的步骤为
- 根据anchor的得分对anchor从高到低进行排序。
- 取出anchor列表(假设有100个anchor)中第一个anchor,计算剩下的所有anchor(99个anchor)与该anchor的iou,将该anchor添加到令一个列表中。
- 舍弃iou大于iou阈值所对应的anchor(认为是检测同一个物体)
- 重复2和3,直至anchor列表为空
代码如下所示
def bbox_iou(anchors1, anchors2):
lt = np.minimum(anchors1[:, np.newaxis, :2], anchors2[:, :2])
rb = np.maximum(anchors2[:, np.newaxis, 2:], anchors2[:, 2:])
inter_area = np.prod(rb - lt, axis=1) * np.all(rb > lt, axis=1)
area1 = np.prod(anchors1[2:] - anchors1[:2], axis=1)
area2 = np.prod(anchors2[2:] - anchors2[:2], axis=1)
return inter_area / (area1[:, np.newaxis] + area2 - inter_area)
def hard_nms(anchors, scores, iou_thresh=0.7, condidates_num=200):
"""
Params:
anchors(numpy.array): detection anchors before nms, with shape(N, 4)
scores(numpy.array): anchor scores before nms, with shape(N, )
iou_thresh(float): iou thershold
Return:
keeps(nump.array): keeped anchor indexes
"""
# if no anchor in anchors
if anchors.size == 0:
return
# sort by scores
idxs = scores.argsort(0)[::-1]
keeps = []
while len(idxs) > 0:
current = idxs[0]
keep.append(current)
# if keeped num equal with condidates_num or only one anchor left
if len(idxs) == 1 or len(keeps) == condidates_num:
break
idxs = idxs[1:]
ious = bbox_iou(anchors[current][np.newaxis, :], anchors[idxs]).flaten()
mask = ious <= iou_thresh
idxs = idxs[mask]
return np.array(keeps)
Soft NMS
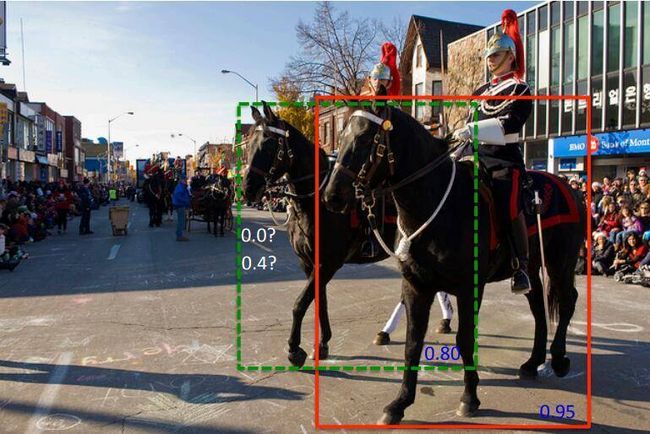
通常我们选择Hard NMS作为目标检测的后处理。但在存在密集物体的情况下Hard NMS会丢弃掉一些在置信度高的anchor周围的anchor。比如下方图片中的两匹马,红色框置信度最高,将会保留下来,假设Hard NMS的iou阈值为0.5,下面红色框和绿色框的iou可能大于阈值,这个时候绿色框将会被丢弃。但在我们看来,绿色框和红色框其实是在检测不同的两匹马,绿色框不应被丢弃。所以这就是Hard NMS所面临的问题。那有没有解决这个问题的方式呢
我们首先可能会想到修改iou阈值来缓解这个问题,那iou阈值到底设置为多少合适呢,设高了,会有产生误检;设低了,召回率会下降,所以这是一个不好抉择的事。
而Soft NMS刚好就是为了解决这个问题的,Soft NMS的过程可以用下图来表示
从上图可以看出NMS(Hard NMS)和Soft NMS唯一的区别在于,处理iou大于阈值对应的anchor的方式,在Hard NMS中,直接把iou大于阈值的anchor丢弃
$$s_i=\begin{cases} & s_i,\quad Iou(M,b_i)< N_t \\&0 ,\quad Iou(M,b_i)\geq N_t \end{cases}$$
而在Soft-NMS中。
$$s_i=\begin{cases} & s_i,\quad Iou(M,b_i)< N_t \\&s_i(1-Iou(M,b_i)) ,\quad Iou(M,b_i)\geq N_t \end{cases}$$
对于上式,它是一个跳跃性变化的函数(小于阈值,score不变,大于阈值,score乘上一个小于1的系数,相当于在$N_t$的位置发生了突变),作者认为该惩罚函数应该是连续的,否则会导致anchor排序的突变。具体参考
因此对上式进行一些改进,变成如下形式
$$s_i=s_ie^{-\frac{iou(M,b_i)^2}{\sigma}},\forall b_i \notin D$$
对于靠近M的anchor的score给予更大的惩罚(penalty),即乘上一个很小的系数,对于远离M的anchor的分值,给予小的惩罚,iou为0,则惩罚为0。
Soft-NMS代码如下
def soft_nms(anchors, scores, iou_thresh=0.7, condidates_num=200, sigma=0.5):
"""
Params:
anchors(numpy.array): detection anchors before nms, with shape(N, 4)
scores(numpy.array): anchor scores before nms, with shape(N, )
iou_thresh(float): iou thershold
sigma(float): soft nms hyper-parameter
Return:
keeps(nump.array): keeped anchor indexes
"""
# if no anchor in anchors
if anchors.size == 0:
return
keeps = []
while len(scores) > 0:
# get the maximum score index
max_idx = np.argmax(scores)
keep.append(max_idx)
# if keeped num equal with condidates_num or only one anchor left
if len(scores) == 1 or len(keeps) == condidates_num:
break
# get the left score indexes
mask = np.arange(len(scores)) != max_idx
scores = scores[mask]
# calculate iou
ious = bbox_iou(anchors[max_idx][np.newaxis, :], anchors[mask]).flaten()
# re-asign value, scores decay
scores = scores * np.exp(-ious * ious / sigma)
scores = scores[scores > iou_thresh]
return np.array(keeps)总结
Soft-NMS是非最大抑制的广义版本,传统NMS是具有不连续二进制加权功能的特殊情况。
从下图可以看出Soft NMS相比于Hard NMS在VOC以及Coco数据集上都有一定提升, 并且Soft NMS并没有增加太多的运算量和超参数,因此还是比较推荐使用的。