NLP --- 隐马尔可夫HMM(概念详解、三个基本问题详解)
本节将进入隐马尔可夫环节,再次提醒不懂马尔科夫过程的同学建议先搞懂什么是马尔科夫过程,什么是马尔科夫链,同时需要懂一点语言模型的知识,下面会用到一点点,本人打算详细总结隐马尔可夫算法思想,因此讲解的会很详细,就意味着我会分几部分来讲,大概思路是先通过浅显易懂的示例引入隐马尔可夫概念,然后给出语音识别的例子引出隐马尔可夫的相关概念和性质,在此基础上深入挖掘HMMs的算法原理和使用过程,以及学习算法思想等等,好,下面正式开始今天的内容。
HMM概念(Hidden markov model)
宗成庆的书里介绍了,利用语言模型进行语音识别的例子,这里我们来简单的看一下这个简单的语音识别是如何使用语言模型进行判别的,他有哪些缺点?这里我们输入是一句话的拼音,要求输出对应的汉子,这就是最简单的语音识别了:
输入: ta shi yan jiu wu li de
输出:塔 是 研究物理的
他式烟酒屋里的
![]()
利用语言模型怎么求呢?其实很简单,就是遍历每个发音多对应的字,然后求出一句话的概率,这样就会求出很多概率的集合,那么我们从中选择概率最大的句子作为输出,这里的难点在哪里呢?难点在计算量上,即每个发音都有很多候选项,例如ta的候选项就有他、它、塔、她、踏、塌、、、等等很多,整个句子的拼音每一个都对应很多的候选项,一旦组合就会出现很多种可能的情况,计算量可想而知,这还是简单的一个句子,如果是很多很长的句子,计算量会呈现指数级增长的,因此语言模型无法解决语音识别的问题,我们就需要研究出更适合语音识别的复杂模型,这时隐马尔可夫就顺势而生了,我们看看隐马尔可夫是如何解决语音识别的问题的。其实很简单,语言模型在计算概率时每个拼音对应的字是独立的即前后没什么关联性,我们知道,我们说的话都和上下文有关的,在常用5000汉子集了,这些汉字的组合大部分都是稀疏的即不能组合的,例如“我们”配对的概率很大,但是“我门”配对的概率很小,基于此HMM模型就根据前面一个或多个字进行对本时刻的发音进行识别,因此可用性很好,从常识中我们也可以很轻松的感受到HMM要比语言模型好很多。到这里我们知道了隐马尔可夫在语音识别的思想了,但是具体他是怎么工作的呢?我们下面就开始来看看。
这里先把隐马尔可夫的定义给出,然后在通过举例进行详细讲解:
一般的,一个HMM记为一个五元组![]() ,其中,S为状态的集合,K为输出符号的集合,
,其中,S为状态的集合,K为输出符号的集合,![]() 分别是初始状态的概率分布、状态转移概率和符号发射概率,为了简单,有时也将其记为三元组
分别是初始状态的概率分布、状态转移概率和符号发射概率,为了简单,有时也将其记为三元组![]() 。下面给大家解释定义都代表什么意思:
。下面给大家解释定义都代表什么意思:
首先你应该知道什么是马尔科夫链,知道什么是转移概率,什么状态,这是你理解下面内容的前提:
在马尔科夫链中,我们有状态转移过程,此过程是可见的即我们可以观察到,如上图的状态转移图,而在隐马尔科夫中的状态转移过程是不可见的如上图的隐藏序列,这里的状态转移概率使用矩阵![]() 表示(和马尔科夫链一样的) ,
表示(和马尔科夫链一样的) ,![]() 是初始的状态概率分布。但是我们在状态转移过程中每个状态会发射一个符合集合中的一个符号,这里我们把符合集合称为K,其中
是初始的状态概率分布。但是我们在状态转移过程中每个状态会发射一个符合集合中的一个符号,这里我们把符合集合称为K,其中![]() ,把状态集合称为S,其中
,把状态集合称为S,其中![]() ,这里还需要强调的是在状态转移的过程中,每到达一个状态就会发射一个符号,这个符号来自符号集合K的任意一个可能情况,因此这里把状态发射的符号的概率集合称为发射概率矩阵
,这里还需要强调的是在状态转移的过程中,每到达一个状态就会发射一个符号,这个符号来自符号集合K的任意一个可能情况,因此这里把状态发射的符号的概率集合称为发射概率矩阵![]() ,这个矩阵
,这个矩阵![]() 是什么样呢?如下:
是什么样呢?如下:
即每个状态都会发射符号集合K中的一个符号,这个符号和发射的概率有关,如在s1状态可能发射![]() 的概率为0.01,可能发射
的概率为0.01,可能发射![]() 的概率为0.08,,,,但是总的概率是1,如上图所示 。
的概率为0.08,,,,但是总的概率是1,如上图所示 。
这里需要强调的是在在隐藏序列里的状态可以发射符号,例如隐藏序列的s1状态发射的符号是![]() ,我们可以观察到的是
,我们可以观察到的是![]() ,但是我们不知道这是哪个状态发射的,这里有点绕,就我们从可观察的序列中的一个符号无法直接得到是哪个状态发射的,这里大家需要理解好。
,但是我们不知道这是哪个状态发射的,这里有点绕,就我们从可观察的序列中的一个符号无法直接得到是哪个状态发射的,这里大家需要理解好。
这里大家可能还会晕晕的,下面我们开始举例子,第一个例子是掷骰子,第二个例子就是我们刚开始简单的语音识别的例子。
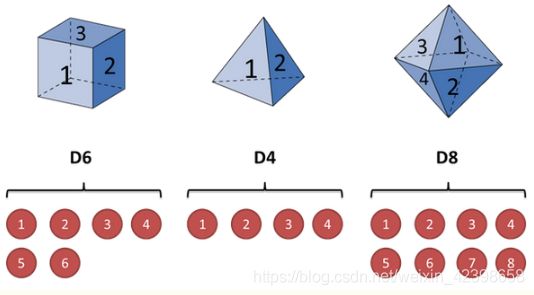
掷骰子:
假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子(称这个骰子为D6),6个面,每个面(1,2,3,4,5,6)出现的概率是1/6。第二个骰子是个四面体(称这个骰子为D4),每个面(1,2,3,4)出现的概率是1/4。第三个骰子有八个面(称这个骰子为D8),每个面(1,2,3,4,5,6,7,8)出现的概率是1/8。
假设我们开始掷骰子,我们先从三个骰子里挑一个,挑到每一个骰子的概率都是1/3。然后我们掷骰子,得到一个数字,1,2,3,4,5,6,7,8中的一个。不停的重复上述过程,我们会得到一串数字,每个数字都是1,2,3,4,5,6,7,8中的一个。例如我们可能得到这么一串数字(掷骰子10次):1 6 3 5 2 7 3 5 2 4
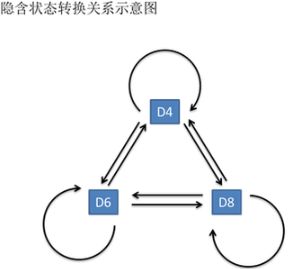
这串数字叫做可见状态链。但是在隐马尔可夫模型中,我们不仅仅有这么一串可见状态链,还有一串隐含状态链。在这个例子里,这串隐含状态链就是你用的骰子的序列。比如,隐含状态链有可能是:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
一般来说,HMM中说到的马尔可夫链其实是指隐含状态链,因为隐含状态(骰子)之间存在转换概率(transitionprobability)。在我们这个例子里,D6的下一个状态是D4,D6,D8的概率都是1/3。D4,D8的下一个状态是D4,D6,D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚,但是我们其实是可以随意设定转换概率的。比如,我们可以这样定义,D6后面不能接D4,D6后面是D6的概率是0.9,是D8的概率是0.1。这样就是一个新的HMM。
同样的,尽管可见状态之间没有转换概率,但是隐含状态和可见状态之间有一个概率叫做输出概率(emission probability)。就我们的例子来说,六面骰(D6)产生1的输出概率是1/6。产生2,3,4,5,6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如,我有一个被赌场动过手脚的六面骰子,掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。
上面就是简单的掷骰子的例子,这个例子在后续的讲解中还需用到,大家需要好好理解,下面在举一个例子是关于语音识别的,当然了下面的例子在后面也是会用到的,所以大家需要留意呀。
语音识别:
上面的例子没有实际意义,所以理解起来可能还是有点困难,这里使用语音识别的例子可能会更好的阐释隐马尔可夫的定义:
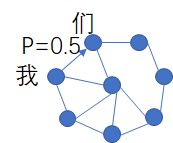
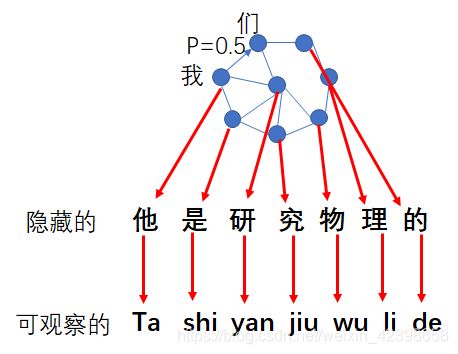
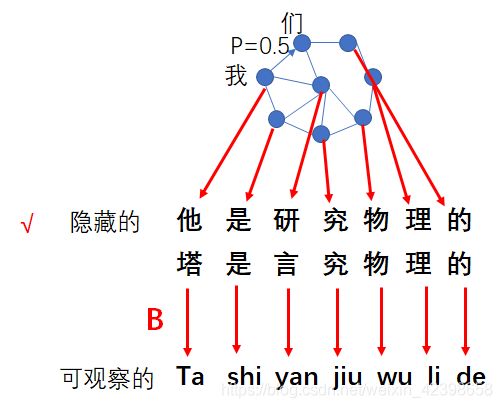
我们知道,所谓语意识别其实就是根据拼音推算出汉子,而常用的汉子有5000多个,这些汉字里的组合很多都是稀疏的,所谓稀疏就是不能组合的例如“天屎”、“霉丽”等,如下图,在常用的组合中我们通过语料库进行计算他们之间的概率,如下是比如汉字间的转移状态,这个状态大概有5000左右,他们之间有转移概率,这个概率是通过语料库计算得到的,例如“我们”,我和们的转移概率达到0.5,因此这些状态构成的转移矩阵将达到5000x5000的规模,其实下图就是我们之前说的概率图模型了又叫状态转移图。
好,上面我们就介绍完了语料库的问题,也就是说状态转移矩阵已经知道了,下面我们详细看看隐马尔可夫的是如何工作的:
上面的拼音是可观察的发射符号,隐藏的是我们未知的序列,现在我们需要通过可观察的符号序列去计算隐藏的序列,也就是去计算状态的转移过程,这就是其中一个隐马尔可夫需要解决的问题,这里大家通过这几个例子应该可以清晰的理解隐马尔可夫的工作过程了吧,这里为了方便,我把上面的定义在拿下来大家再看看:
一般的,一个HMM记为一个五元组![]() ,其中,S为状态的集合,K为输出符号的集合,
,其中,S为状态的集合,K为输出符号的集合,![]() 分别是初始状态的概率分布、状态转移概率和符号发射概率,为了简单,有时也将其记为三元组
分别是初始状态的概率分布、状态转移概率和符号发射概率,为了简单,有时也将其记为三元组![]() 。
。
当考虑潜在事件随机的生成表面事件时,HMM是非常有用的,假设给定模型![]() ,那么观察序列
,那么观察序列![]() 可以由下面的步骤直接产生:
可以由下面的步骤直接产生:
(1)根据初始状态的概率分布选择一个初始状态![]() ;
;
(2)设t=1;
(3)根据状态![]() 的输出概率分布
的输出概率分布![]() 输出
输出![]() ;
;
(4)根据状态转移概率分布![]() ,当前时刻t的状态转移到新的状态
,当前时刻t的状态转移到新的状态![]() ;
;
(5)t = t+1,如果t 上面我们知道了隐马尔可夫是什么,但是不知道隐马尔可夫是干什么的,下面将详细介绍HMM是干什么的,他有什么用,有什么优缺点等,首先就是先介绍隐马尔可夫是干什么的,他可以解决三种不同的问题,下面我们来看看: 三个基本问题: (1) 估计问题:给定一个观察序列 我们先从第一个问题开始讲解: 第一个问题 1) 估计问题:给定一个观察序列 这里把我们上一节的例子直接拿过来使用了,不懂的请查看NLP --- 隐马尔可夫HMM(概念详解),如果使用掷骰子的例子是什么意思呢?其实就是: 1)知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次 掷出来的都是哪种骰子(隐含状态链)。 上面的例子可能没有实际的意义,下面把语音识别的那个简单的例子拿过来进行解释: 这里的任务呢就是我们语音输入得到可观察的序列,但是存在这样一个问题就是如果说话者普通话不标准或者环境干扰大,此时假如把ta发音te了,那么我们需要计算得到的可观察序列的概率有多大,而且我们把最大的那个当做本次的正确输入,例如如果本次输入的是下面一行的语音,但是通过解码后发现上面一行的概率最大, 因此就把上面的一行当做正确的语音输入。因此这就是第一个基本问题了,用处在语音识别中很明显。 第二个问题 (2)序列问题:给定一个观察序列 先使用掷骰子的例子说明一下: 2)还是知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。 这里还是还是语音识别的例子进行解释更容易理解,如下: 这里先默认语音的输入是正确的,如可观察序列是标准正确的,那么我们现在想通过可观察的序列即拼音,去寻找一个对应的文字(这就是语音识别的任务了),那么对应的句子那么多,哪个才是正确的呢?其实就是转态转移概率最大的那个句子就是最优的 ,如上图,隐藏层的第一行的汉子就是很好的“解释”了拼音且概率是最大的,而第二行就不是很好的解释,概率当然不是最大的,因此第二个基本问题就是这个意思,至于如何求这个概率,我们后面会讲解。 第三个问题 (3)训练问题或参数估计问题:给定一个观察序列 掷骰子解释就是: 3)知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)。 使用语音识别的进行解释更形象点,在语音识别中对应着发射概率B,如上图中的B,这里有什么歧义的呢?最明显的是多音字如“给”既可以是读“gei”,又可以读“gi”,这各无法计算这个两个的概率,因此对应着发射概率问题,这个问题在后面通过期望最大化算法进行解决,当然也有可能是状态矩阵的参数不确定等问题,这里大家应该都可以理解了,这些问题将主导后面的学习,因为我们就围绕这三个问题解决而展开的。 下面应该进行这三个问题的求解了,本打算直接接着往下写的,但是想想内容太多了,如果写在一篇博客中会显得特别的庸长,所有打算单独开一篇博客进行总结,还有下一节会把前两个问题解决掉,前两个问题相对来说简单点,但是第三个问题就麻烦了牵扯到EM(期望最大化算法)算法,会很麻烦,想要理解EM首先就是需要理解什么是最大释然估计,所以后面的文章会把前两个问题解决了,然后简单提一下第三问的难点在哪里,指明为什么要使用EM算法,然后开始从最大释然估计讲起,在引入EM算法,最后在给出解决第三个问题的方法,这样会更好点。 所以本节内容有点少,下一节将进入难点。 参考书籍:宗成庆的《统计自然语言处理》 参考博客:http://www.cnblogs.com/skyme/p/4651331.html![]() 和模型
和模型![]() ,如何快速地计算出给定模型
,如何快速地计算出给定模型![]() 情况下,观 察序列
情况下,观 察序列![]() 的概率,即
的概率,即![]() ?
?
(2)序列问题:给定一个观察序列![]() 和模型:
和模型:![]() ,如何快速有效地选择在一定意义下“最 优”的状态序列
,如何快速有效地选择在一定意义下“最 优”的状态序列![]() ,使得该状态序列“最好地解释”观察序列?
,使得该状态序列“最好地解释”观察序列?
(3)训练问题或参数估计问题:给定一个观察序列![]() ,如何根据最大似然估计来求模型的参数值?即如 何调节模型
,如何根据最大似然估计来求模型的参数值?即如 何调节模型![]() 的参数,使得
的参数,使得![]() 最大?
最大?![]() 和模型
和模型![]() ,如何快速地计算出给定模型
,如何快速地计算出给定模型![]() 情况下,观察 序列
情况下,观察 序列![]() 的概率,即
的概率,即![]() ?其实这个问题称为解码问题。
?其实这个问题称为解码问题。
这个问题呢,在语音识别领域呢,叫做解码问题。这个问题其实有两种解法,会给出两个不同的答案。每个答案都对,只不过这些答案的意义不一样。第一种解法求最大似然状态路径,说通俗点呢,就是我求一串骰子序列,这串骰子序列产生观测结果的概率最大。![]() 和模型:
和模型:![]() ,如何快速有效地选择在一定意义下“最 优”的状态序列
,如何快速有效地选择在一定意义下“最 优”的状态序列![]() ,使得该状态序列“最好地解释”观察序列?
,使得该状态序列“最好地解释”观察序列?
看似这个问题意义不大,因为你掷出来的结果很多时候都对应了一个比较大的概率。问这个问题的目的呢,其实是检测观察到的结果和已知的模型是否吻合。如果很多次结果都对应了比较小的概率,那么就说明我们已知的模型很有可能是错的,有人偷偷把我们的骰子給换了。![]() ,如何根据最大似然估计来求模型的参数值?即如 何调节模型
,如何根据最大似然估计来求模型的参数值?即如 何调节模型![]() 的参数,使得
的参数,使得![]() 最大?
最大?
这个问题很重要,因为这是最常见的情况。很多时候我们只有可见结果,不知道HMM模型里的参数,我们需要从可见结果估计出这些参数,这是建模的一个必要步骤。