机器学习sklearn（11）神经网络

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import StandardScaler
%matplotlib inline

#导入数据集

data_MLP = pd.read_csv('data_MLP.csv', header=None)
print(data_MLP)

          0          1  2
0  -0.017612  14.053064  0
1  -1.395634   4.662541  1
2  -0.752157   6.538620  0
3  -1.322371   7.152853  0
4   0.423363  11.054677  0
5   0.406704   7.067335  1
6   0.667394  12.741452  0
7  -2.460150   6.866805  1
8   0.569411   9.548755  0
9  -0.026632  10.427743  0
10  0.850433   6.920334  1
11  1.347183  13.175500  0
12  1.176813   3.167020  1
13 -1.781871   9.097953  0
14 -0.566606   5.749003  1
15  0.931635   1.589505  1
16 -0.024205   6.151823  1
17 -0.036453   2.690988  1
18 -0.196949   0.444165  1
19  1.014459   5.754399  1
20  1.985298   3.230619  1
21 -1.693453  -0.557540  1
22 -0.576525  11.778922  0
23 -0.346811  -1.678730  1
24 -2.124484   2.672471  1
25  1.217916   9.597015  0
26 -0.733928   9.098687  0
27  1.416614   9.619232  0
28  1.388610   9.341997  0
29  0.317029  14.739025  0

data = np.array(data_MLP)
data_x = data[:,:-1]
data_label = data[:,-1]

#神经网络对数据尺度非常敏感，所以在训练前先进行标准化
scaler = StandardScaler()
scaler.fit(data_x)
X = scaler.transform(data_x)

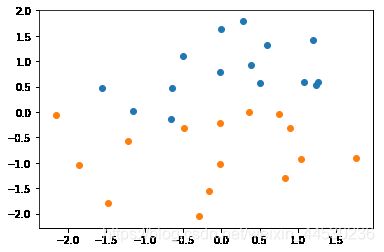
#对标准化后的数据集可视化

plt.scatter(X[data_label==0,0], X[data_label==0,1])
plt.scatter(X[data_label==1,0], X[data_label==1,1])
plt.show()

#训练数据集
clf = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(5,2), random_state=1)
clf.fit(X, data_label)
y_pred = clf.predict([[0.317029, 14.739025]])
print("预测结果: ", y_pred)

预测结果:  [0.]

y_pred_pro = clf.predict_proba([[0.317029, 14.739025]])
print("预测结果概率: ", y_pred_pro)

预测结果概率:  [[1.00000000e+000 6.63279745e-305]]

n = 0
for w in clf.coefs_:
    n += 1
    print("第%d层神经网络: "%n)
    print("权重矩阵维度: ", w.shape)
    print("系数矩阵: ", w)

第1层神经网络: 
权重矩阵维度:  (2, 5)
系数矩阵:  [[-1.09538274  0.36309949 -1.27227154 -0.39894637 -0.15406402]
 [-0.50033282 -1.97053658 -1.39997854  4.38015871  0.30071309]]
第2层神经网络: 
权重矩阵维度:  (5, 2)
系数矩阵:  [[-0.60507595 -0.25381544]
 [-2.00854543 -0.67673634]
 [-2.07756639  0.12092846]
 [ 2.90811389 -0.49062085]
 [ 0.22256248  0.64391743]]
第3层神经网络: 
权重矩阵维度:  (2, 1)
系数矩阵:  [[-3.68728924]
 [-0.88764417]]

#绘制分割区域
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 # 确定x轴的范围
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 # 确定y轴的范围

# meshgrid：常用于生成网格点采样点，根据传入的两个一维数组参数生成两个数组元素的列表。
# 如果第一个参数是xarray，维度是xdimesion，第二个参数是yarray，维度是ydimesion。
# 那么生成的第一个二维数组是以xarray为行，共ydimesion行的向量；而第二个二维数组是以yarray的转置为列，共xdimesion列的向量。
xx1, xx2 = np.meshgrid(np.arange(x_min, x_max, 0.01),np.arange(y_min, y_max,0.01)) 

#np.reavel()将多维数组降位一维
#np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等。
Z = clf.predict(np.c_[xx1.ravel(), xx2.ravel()])

Z = Z.reshape(xx1.shape) # 将输出结果转换为和网格点一样的矩阵形式，以便绘图

# 绘制区域网格图
plt.pcolormesh(xx1, xx2, Z, cmap=plt.cm.Paired)   #paired表示两个两个相近色彩输出，比如浅蓝、深蓝；浅绿，深绿这种
plt.scatter(X[:,0],X[:,1],c=data_label)
plt.show()