由于本人的算法基础较为薄弱,所以在这里整理一下自己的做过的题,使自己能够随时随地回顾温习。然后,本篇文章将会持续更新自己遇到的一些比较经典动态规划的题目,大家如果对代码有任何问题,直接在文章下面评论即可。我看到后会立刻回复。
1.我对动态规划的理解
网上对动态规划的介绍的文章已经很多了,那这里我还是要谈一下自己的理解,希望能够给大家带来一些灵感。
我所理解的动态规划,就两个词:动态、规划。动态我自己理解为:一个问题可以拆分为若干个子问题,然后通过逐步递推,得到最终的结果。规划就是最优问题,整体的最优细分到每个递推环节的最优。
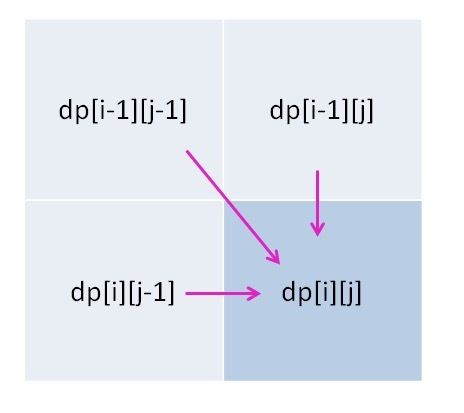
然后,解决动态规划问题,最重要的可以发现其中的状态转移方程,我理解的状态转移方程的意思就是:一个通用的方程,即任意中间一个状态能够由前面的状态所推导得到。比如下图的dp[i][j]状态,就可以由左上的3个状态推导得到。
很多动态规划的问题,具体解法大多都是通过一个二维数组来存储中间环节的最优解。最后求二维数组中的最大值或者最后一个值。还有一种情况就是:如果当前状态只跟前面的一个状态有关,那么二维数组是可以优化为一维数组的,这样空间复杂度就由O(n2)优化为O(n)了。
2.例题整理
2.1 经典01背包问题
题目描述:一个人去偷东西,他的背包容量最大为20kg,然后有重量、价值不等的物品,比如重量为2、价值为3的物品,每件物品只能拿一件,求小偷能偷到的物品最大的价值。
"""
物品重量与价值对应关系:
w v
2 3
3 4
5 8
9 10
背包容量:20
"""
import numpy as np
def func(pack, cap):
max_value_arr = np.zeros([len(pack)+1, cap+1])
# 第一列与第一排全为0,这样为后续能递推max_value_arr的值
max_value_arr[:,0] = 0
max_value_arr[0,:] = 0
# i代表pack物品的序号
for i in range(1, len(pack)+1):
# j代表包中剩余的空间
for j in range(1, cap+1):
# 第一种情况,包中剩余空间不足
if j < pack[i-1][0]:
max_value_arr[i, j] = max_value_arr[i-1, j]
# 第二种情况,包中空间足够
else:
# a代表放入当前物品后包中总价值,w是当前物品的所占空间
w = pack[i-1][0]
"""
下面这行是关键!!!为什么是i-1,这里必须用i-1才能推出当前的max_value_arr的值,
然后再加上单独的value
"""
a = max_value_arr[i-1, j-w] + pack[i-1][1]
# b代表不放当前物品包中的总价值,两者求最大值
b = max_value_arr[i-1, j]
max_value_arr[i, j] = max(a, b)
print(max_value_arr[-1, -1])
test_pack = [[2, 3],
[3, 4],
[4, 5],
[5, 8],
[9, 10]]
func(test_pack, 20)
2.2 最长公共子串
题目描述:a b两个字符串,求a b的最长公共子串。子串与子序列不同,子串必须是连续的,而子序列可以不连续。例如:
输入: a="abccbca",b="bccca"
输出: 3
解释: 最长公共子序列就是"bcc",为3# 动态规划:只有当a[i-1]==b[j-1]时,子串长度才会在i-1与j-1的基础上+1
# 如果不同,则不变。用变量来记录表中最大的子串长度
a = "abccccdd"
b = "abcabcbbccs"
la = len(a)
lb = len(b)
res = [[0 for i in range(lb+1)] for j in range(la+1)]
mmax = 0
for i in range(1, la+1):
for j in range(1, lb+1):
if a[i-1] == b[j-1]:
res[i][j] = res[i-1][j-1] + 1
mmax = max(res[i][j], mmax)
print(mmax)
2.3 最长公共子序列(Leetcode1143)
题目描述:a b两个字符串,求a b的最长公共子序列。这里与上一题要区分开,重点是子序列可以是不连续的。
输入: a="abccbca",b="bccca"
输出: 6
解释: 最长公共子序列就是"bccca",为6# 动态规划:相等就+1
# 如果不相等,则是max(a字符串少一个字符,b字符串少一个字符)
a = "abccccdd"
b = "abcabcbbcs"
la = len(a)
lb = len(b)
res = [[0 for i in range(lb+1)] for j in range(la+1)]
for i in range(1, la+1):
for j in range(1, lb+1):
if a[i-1] == b[j-1]:
res[i][j] = res[i-1][j-1] + 1
else:
res[i][j] = max(res[i-1][j], res[i][j-1])
print(res[-1][-1])
2.4 最大子序和(Leetcode53)
题目描述:给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。例如:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。# 每项为:以此项为结尾的最大子序和
# 如果前一项的子序和<0,那么此项结尾的最大子序和就是本身
# 如果前一项的子序和>0,那么此项结尾的最大子序和就是前一项加上本身
def maxSubArray(nums):
l = len(nums)
res = [0 for i in range(l)]
for i in range(l):
if i == 0:
res[i] = nums[i]
else:
if res[i - 1] <= 0:
res[i] = nums[i]
else:
res[i] = nums[i] + res[i - 1]
return max(res)
2.5 最长上升子序列(Leetcode300)
题目描述:给定一个无序的整数数组,找到其中最长上升子序列的长度。例如:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。# 最长上升子序列(动态规划)
# res[i]代表以此项为结尾的最大上升子序列的长度
# 关键是,拿当前值nums[i]与前面的值nums[j]相对比
# 如果比它大,那么就可以在res[j]的基础上加1。最后判断遍历完nums前j个元素后,加一的最大值,作为res[i]
def lengthOfLIS(nums):
l = len(nums)
if l == 0:
return 0
res = [1 for i in range(l)]
for i in range(l):
max_ = 1
temp = 0
for j in range(i):
if nums[i] > nums[j]:
temp = res[j] + 1
if temp > max_:
max_ = temp
res[i] = max_
return res
nums = [10,9,2,5,3,7,101,1]
print(lengthOfLIS(nums))
# 2,3,7,101 max为4
2.6 摆动序列(Leetcode376)
题目描述:如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。例如:
输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。# 这题分为,如果上一次的摆动时正时,那么如果此次为负摆动的时候,最长摆动序列为上一次的最长摆动序列加1,
# 如果此次为正摆动或者没有摆动时,最长摆动序列就是上一次的最长摆动序列数;如果上一次摆动为负时,那么
# 如果此次为正摆动的时候,最长摆动序列为上一次的最长摆动序列加1,如果此次为负摆动或者没有摆动时,最长
# 摆动序列就是上一次的最长摆动序列数。用数组来记录这些上一次的最长摆动序列,方便以后使用。
test_list = [1, 17, 3, 20, 15, 6, 7, 8]
def swing(test):
if len(test) < 2:
return len(test)
up = 1
down = 1
idx = 1
n = len(test)
while idx < n:
if test[idx] > test[idx-1]:
up = down + 1
if test[idx] < test[idx-1]:
down = up + 1
idx += 1
return max(up, down)
print(swing(test_list))
2.7 最小路径和(Leetcode64)
题目描述:给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。注意:每次只能向下或者向右移动一步。
这个题很常见,面试经常被问到。
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。def minPathSum(grid):
for i in range(len(grid)):
for j in range(len(grid[0])):
if i == j == 0:
continue
elif i == 0:
grid[i][j] = grid[i][j - 1] + grid[i][j]
elif j == 0:
grid[i][j] = grid[i - 1][j] + grid[i][j]
else:
grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j]
return grid[-1][-1]