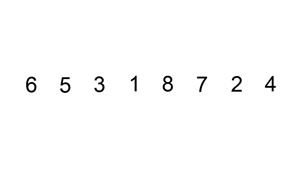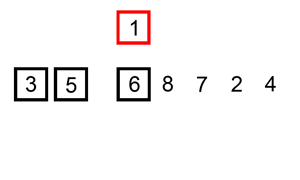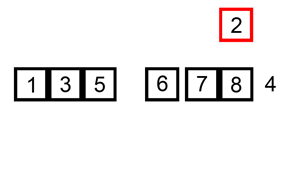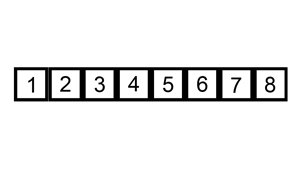python算法图解——快速排序和选择排序

分而治之

一种著名的递归式问题解决方法:分而治之。（divide and conquer，D&C）。
D&C的工作原理：
(1) 找出简单的基线条件；
(2) 确定如何缩小问题的规模，使其符合基线条件
基线条件的要求：编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素。陷入困境时，检查基线条件是不是这样的。
例题1：编写一个递归函数来计算列表包含的元素数的和

def sum(list):
    if list == []:
        return 0
    else:
        return list[0] + sum(list[1:])

合并两个列表 可以直接进行相加

快速排序

快速排序用一种分而治之的思想，
快速排序的步骤：
(1) 选择基准值。
(2) 将数组分成两个子数组：小于基准值的元素和大于基准值的元素。
(3) 对这两个子数组进行快速排序。
快速排序的例子(采用了递归的思想)：
算法简单描述：选择数组第一位元素位基准值，创建两个新数组，分别存放小于基准值和大于基准值的元素。然后这两个新数组递归进行上述操作，直到数组为空。然后将左右数组和基准值进行拼接

def quicksort(array):
  if len(array) < 2:
    # 基线条件：为空或只包含一个元素的数组是“有序”的
    return array
  else:
    pivot = array[0]
    # 由所有小于基准值的元素组成的子数组
    less = [i for i in array[1:] if i <= pivot]
    # 由所有大于基准值的元素组成的子数组
    greater = [i for i in array[1:] if i > pivot]

    return quicksort(less) + [pivot] + quicksort(greater)

选择排序

选择排序的步骤：遍历，找到一个最小的值，然后将其加入一个新的列表，循环
每次选择最小的元素，放在相应的位置上

@pysnooper.snoop()
def findSmallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(1, len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index


@pysnooper.snoop()
def selectionSort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = findSmallest(arr)
        newArr.append(arr.pop(smallest))
    return newArr

print(selectionSort([5, 3, 6, 2, 10]))

冒泡排序

相邻元素进行比较，每次选取最大的元素，进行下一次比较，因此可以将最大的元素像冒泡一样，从某一位置，到达最顶端。
冒泡排序算法的运作如下：
①比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
②针对所有的元素重复以上的步骤，除了最后一个。持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

@pysnooper.snoop()
def bubble_sort(alist):
    for j in range(len(alist) - 1, 0, -1):
        # j表示每次遍历需要比较的次数，是逐渐减小的
        for i in range(j):
            if alist[i] > alist[i + 1]:
                # 大的话交换位置
                alist[i], alist[i + 1] = alist[i + 1], alist[i]

li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
bubble_sort(li)
print(li)

插入排序

将数组分为前后两部分，前一部分是已排序的元素集合，后一部分是未排序的元素集合。每次选中未排序的第一个数组，插入到已排序集合中的合适的位置。
工作原理：是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，也就是进行比较，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。和冒泡排序类似

def insert_sort(alist):
    # 从第二个位置，即下标为1的元素开始向前插入
    for i in range(1, len(alist)):
        # 从第i个元素开始向前比较，如果小于前一个元素，交换位置
        for j in range(i, 0, -1):
            if alist[j] < alist[j - 1]:
                alist[j], alist[j - 1] = alist[j - 1], alist[j]
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
insert_sort(alist)
print(alist)

希尔排序

希尔排序就是插入排序的优化，插入排序，每次将当前元素与之前的每一个元素进行比较，然后插入，希尔排序，相当于先按照一定步长，将数组进行分组，对每一组进行插入排序，这样就可以大幅度的调整数据的分布情况，最后执行一次快速排序进行微调
基本思想：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样(竖着的元素是步长组成)：

def shell_sort(alist):
    n = len(alist)
    # 初始步长
    gap = int(n / 2)
    while gap > 0:
        # 按步长进行插入排序
        for i in range(gap, n):
            j = i
            # 插入排序
            while j >= gap and alist[j - gap] > alist[j]:
                alist[j - gap], alist[j] = alist[j], alist[j - gap]
                j -= gap
        # 得到新的步长
        gap = int(gap / 2)
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
shell_sort(alist)
print(alist)

归并排序

自顶向下：先通过递归分解数组，再合并数组
算法简单描述：
　　分解数组：如果数组长度不为1，从中间将数组分为两部分，继续分解
　　合并数组：将分解的数组融合，创建一个新数组，用于存放融合的数组元素。创建指针分别指向两个数组的首位，比较当前指针指向位置元素的大小，将较小的元素插入新数组中，指针向后移动，直到有一个数组元素全部移出。最后检查两个数组，将未移出的元素追加到新数组中，最后存放已排序的数组根据对应位置存入待排序数组中。
　　

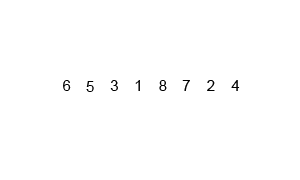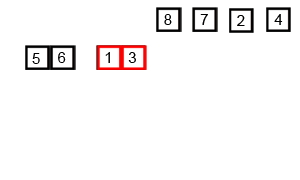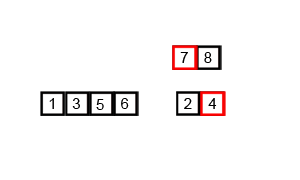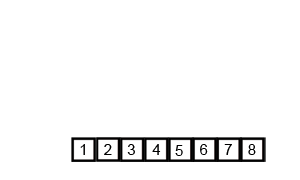
def merge_sort(alist):
    if len(alist) <= 1:
        return alist
    # 二分分解
    num = int(len(alist) / 2)
    left = merge_sort(alist[:num])
    right = merge_sort(alist[num:])
    # 合并
    return merge(left, right)

def merge(left, right):
    '''合并操作，将两个有序数组left[]和right[]合并成一个大的有序数组'''
    # left与right的下标指针
    l, r = 0, 0
    result = []
    while l < len(left) and r < len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]
    result += right[r:]
    return result
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
sorted_alist = merge_sort(alist)
print(sorted_alist)

链接: 几种排序算法.