零基础入门数据挖掘 Task02：数据的探索性分析（EDA）

Task02：数据的探索性分析（EDA）

赛题：零基础入门数据挖掘 - 二手车交易价格预测
地址：https://tianchi.aliyun.com/competition/entrance/231784/information

参考资料

探索性数据分析
数据处理之二——数据探索性分析（EDA）
探索性数据分析(EDA)

1 EDA目标

探索性数据分析（Exploratory Data Analysis，EDA）是指对已有数据在尽量少的先验假设下通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。常用的手段包括定量分析和可视化技术。

EDA常用的一些常见问题：

1. 数据的典型值是多少(均值，中位数等)？
2. 典型值的不确定性是什么？
3. 一组数据的良好分布拟合是什么？
4. 数据的分位数是多少？
5. 一个工程上的修改是否有作用？
6. 一个因子是否有影响？
7. 最重要的因素是什么？
8. 来自不同实验室的测量结果是否相等？
9. 将响应变量与一组因子变量相关联的最佳函数是什么？
10. 什么是最好的因子设置？
11. 我们可以将时间相关数据中的信号与噪声分离吗？
12. 我们可以从多变量数据中提取任何结构吗？
13. 数据是否有离群值？

通过EDA可以实现：

1. 得到数据的直观表现
2. 发现潜在的结构
3. 提取重要的变量
4. 处理异常值
5. 检验统计假设
6. 建立初步模型
7. 决定最优因子的设置

2 代码示例

2.1 载入各种数据科学以及可视化库:

• pandas是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。Pandas纳入了大量库和一些标准的数据模型，提供了高效地操作大型数据集所需的工具。pandas提供了大量能使我们快速便捷地处理数据的函数和方法。
• NumPy是使用Python进行科学计算的基础包, 代表 “Numeric Python”。它是一个由多维数组对象和用于处理数组的例程集合组成的库，多用在大型,多维数组上执行数值运算。
• Matplotlib 是一个 Python 的 2D绘图库，它以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形。直方图，功率谱，条形图，错误图，散点图等。pyplot是Matplotlib 软件包中子包，提供了一个类似MATLAB的绘图框架。
• Seaborn是在matplotlib的基础上进行了更高级的API封装，从而使得作图更加容易，在大多数情况下使用seaborn能做出很具有吸引力的图，而使用matplotlib就能制作具有更多特色的图。应该把Seaborn视为matplotlib的补充，而不是替代物。
• missingno库提供了一个灵活易用的可视化工具来观察数据缺失情况，是基于matplotlib的，接受pandas数据源

#导入warnings包，忽略警告语句
import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno 

2.2载入数据：

• read_csv读文件方式，默认是以逗号“，”作为分割符；若是以其它分隔符，比如制表符“/t”，则需要显示的指定分隔符。如：pd.read_csv(filename,sep=’/t’)

#载入数据集和测试集
#这里的sep=‘ ’指的是将分隔符设为空格
Train_data = pd.read_csv('used_car_train_20200313.csv', sep=' ')
Test_data = pd.read_csv('used_car_testA_20200313.csv', sep=' ')

• 简略观察数据（要养成看数据集的head()以及shape的习惯）

#简略观察数据(head()+shape)
#head():观察前五行数据; tail():观察后五行数据
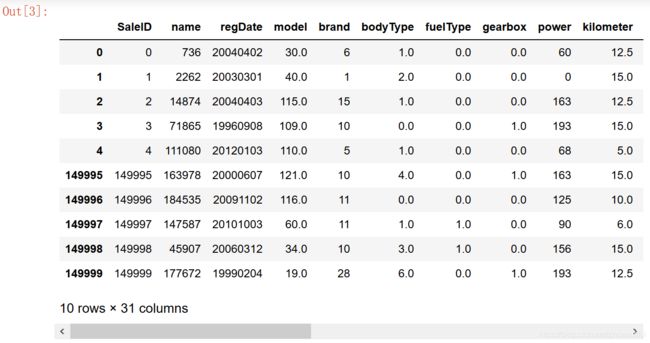
Train_data.head().append(Train_data.tail()) 

Train_data.shape

下面是查看测试集的head()以及shape，结果略。

Test_data.head().append(Test_data.tail()) 
Test_data.shape

2.3数据总览:

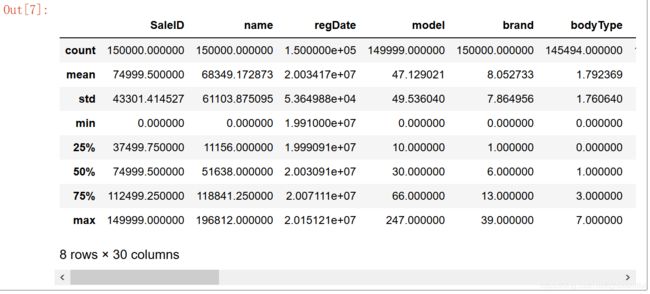
• describe中有每列的统计量，个数count、平均值mean、方差std、最小值min、中位数25% 50% 75% 、以及最大值 看这个信息主要是瞬间掌握数据的大概的范围以及每个值的异常值的判断，比如有的时候会发现999 9999 -1 等值这些其实都是nan的另外一种表达方式，有的时候需要注意下。
  • 格式：describe( percentiles=None, include=None, exclude=None)
  • 注：include=‘all’,代表对所有列进行统计，如果不加这个参数，则只对数值列进行统计
• info通过info来了解数据每列的type，有助于了解是否存在除了nan以外的特殊符号异常

#通过describe()来熟悉数据的相关统计量
Train_data.describe()

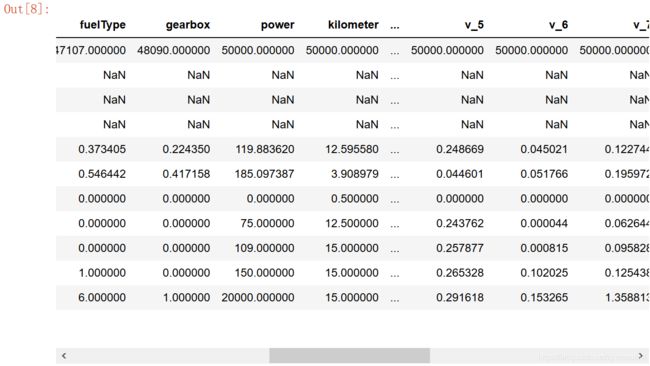
这里试了下用include='all’这个参数，得知describe（）统计出的列是不一样的，会将所有类型的列都进行统计，包括object类型。如没有，则只对数值列进行统计。

# include='all',代表对所有列进行统计，如果不加这个参数，则只对数值列进行统计(notRepairedDamage列是object类型)
Test_data.describe(include='all')  

#通过info()来熟悉数据类型
Train_data.info() 
Test_data.info()

结果略。

2.4判断数据缺失和异常

• .isnull().sum()将列中为空的个数统计出来，即，计算缺省值

#看每列的存在nan情况
#使用isnull()函数得到true或者false
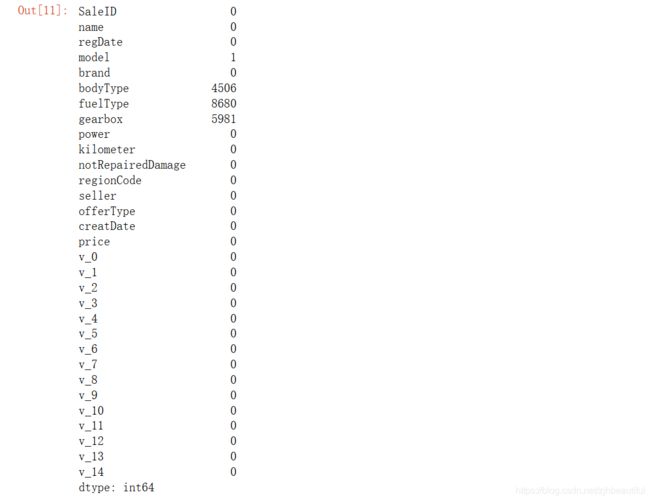
Train_data.isnull().sum()
Test_data.isnull().sum()

Test_data.isnull().sum()

• 接下来对含有nan的信息进行可视化
  • 这里使用了sort_value函数来进行排序，默认为升序排序；设置inplace=True用排序后的数据集替换原来的数据，默认False是不替换
  • 直观的了解哪些列存在 “nan”的主要目的在于看 nan存在的个数是否真的很大，如果很小一般选择填充，如果使用lgb等树模型可以直接空缺，让树自己去优化，但如果nan存在的过多、可以考虑删掉

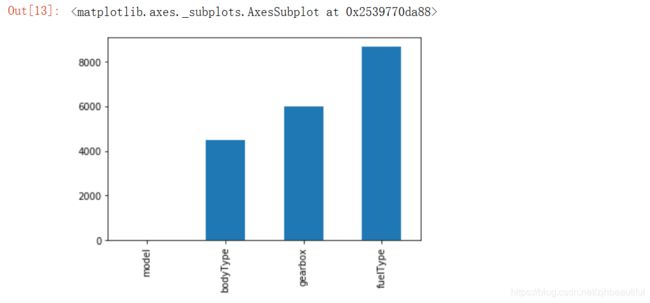
# nan可视化
missing = Train_data.isnull().sum()
missing = missing[missing>0]
missing.sort_values(inplace=True) 
missing.plot.bar()

• 可视化缺省值

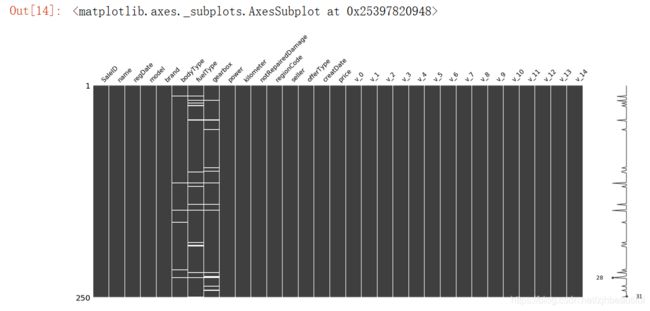
# 可视化看下缺省值
msno.matrix(Train_data.sample(250)) # sample（250）表示抽取表格中250个样本

上图是代码运行后得到的结果，白线越多，代表缺失值越多

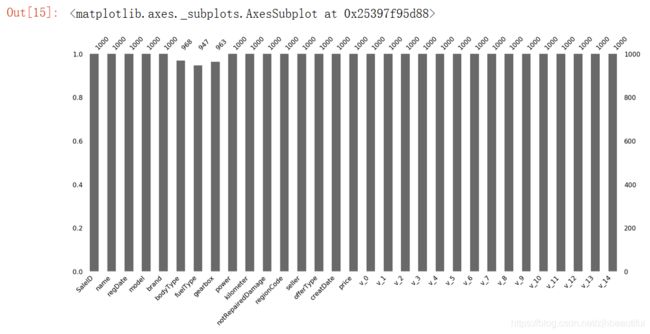
msno.bar(Train_data.sample(1000))

利用条形图可以更直观的看出每个变量缺失的比例和数量情况。

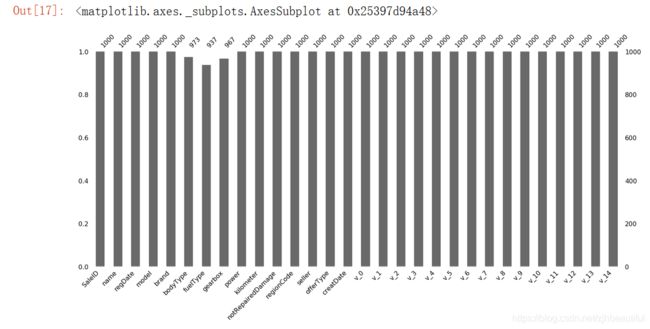
msno.matrix(Test_data.sample(250))

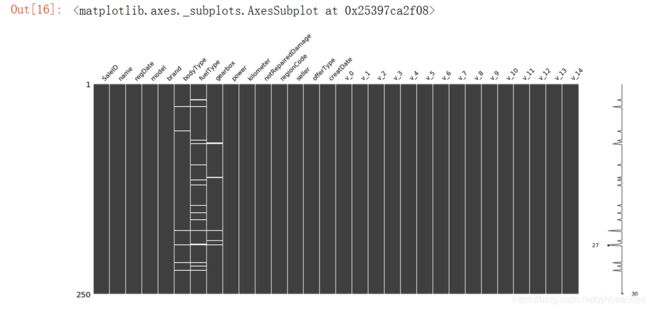
我们可以一目了然的看到每个变量的缺失情况：测试集的缺省和训练集的差不多情况, 可视化有三列有缺省，fuelType缺省得最多, 参考缺失值可视化处理–missingno

msno.bar(Test_data.sample(1000))

• 异常值检测

Train_data.info()

还记得前面的describe()统计信息时，由于notRepairedDamage列是object类型，所以没有统计进去。所以，当发现有object类型的字段时，应该单独拿出来看一下其取值情况，以防存在数值脏乱情况，应该对数据保持一种怀疑的态度，以防人为标注的时候出现的错误等。数据的检查与修正还是挺重要的， 可参考数据竞赛修炼笔记之工业化工生产预测

# 看看object这个字段的取值情况
Train_data['notRepairedDamage'].value_counts()

可以看出里面有个’-’，这个也代表着缺失。因为很多模型对nan有直接的处理， 这里我们可以先不做处理，先替换为nan，所以字符串类型的要小心缺失的，格式不规范的情况大有存在，格式不规范的情况可以看 数据竞赛修炼笔记之工业化工生产预测，从那这面可真正体会到怀疑数据的重要性。

#将-替换成nan
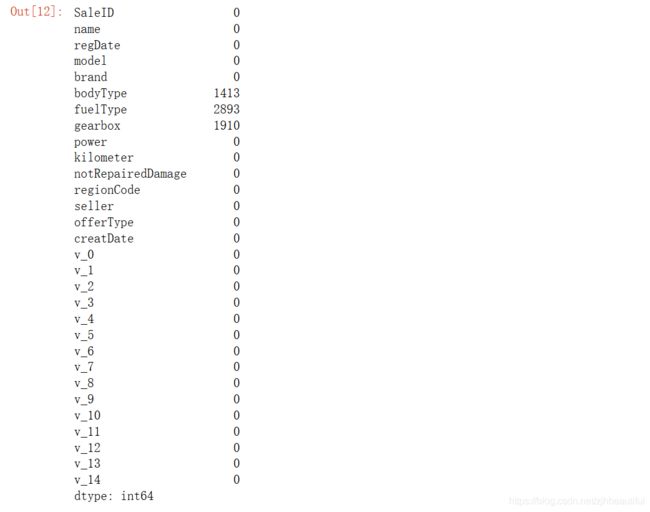
Train_data['notRepairedDamage'].replace('-', np.nan, inplace=True)

#重新查看缺省值
Train_data.isnull().sum()

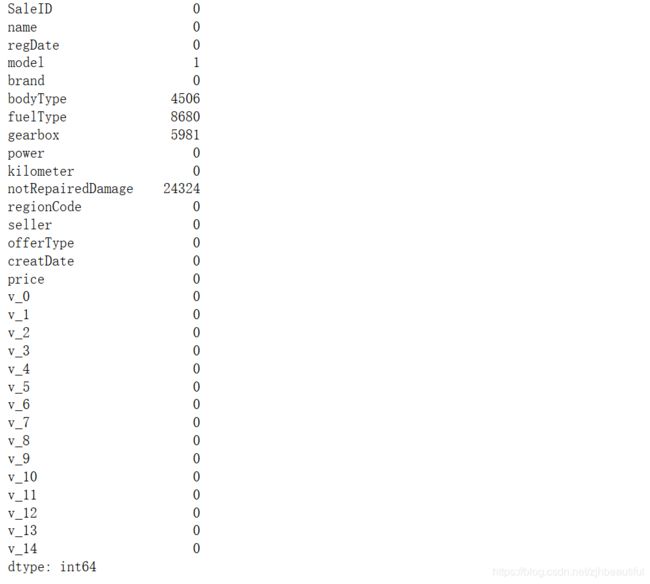
这时，发现缺省值最多的是这个notRepairedDamage字段。

# 对测试集进行同样的操作
Test_data['notRepairedDamage'].replace('-',np.nan,inplace=True)

# 观察其他数据
Train_data["seller"].value_counts()

# 观察其他数据
Train_data["offerType"].value_counts()

以上两个类别特征严重倾斜（销售方几乎为个体，报价类型全部为提供），一般不会对预测有什么帮助，故这边先删掉

del Train_data['seller']
del Train_data['offerType']
del Test_data['seller']
del Test_data['offerType']

2.5 了解预测值的分布

Train_data['price'].value_counts()

从上面统计可以看出price的分布不均匀，所以接下来通过画图来可视化一下

#直方图可视化一下
plt.hist(Train_data['price'])
plt.show()

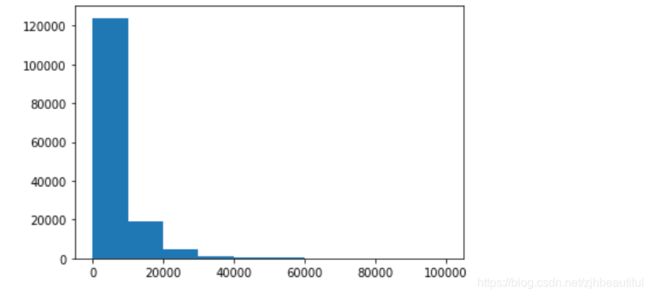
从图中可以看出，频数里大于20000的值极少，所以这里也可以把这些当作特殊得值（异常值）直接用填充或者删掉，再往下进行。不过直接删掉有点风险，毕竟这是个回归问题，得出的效果可能很差，需要在baseline中试一下。

#总体分布概况(无界约翰逊分布等)
import scipy.stats as st
y = Train_data['price']

plt.figure(1)
plt.title('Johnson SU')
sns.distplot(y,kde=False,fit=st.johnsonsu)

plt.figure(2)
plt.title('Normal')
sns.distplot(y,kde=False,fit=st.norm)

plt.figure(3)
plt.title('Log Normal')
sns.distplot(y,kde=False,fit=st.lognorm)

seaborn中的distplot主要功能是绘制单变量的直方图，该函数结合了matplotlib中的 hist函数（自动计算一个默认的合适的bin大小）、seaborn的kdeplot()和rugplot()函数。它还可以拟合scipy.stats分布并在数据上绘制估计的PDF（概率分布函数）。

• kde：bool型变量，控制是否绘制高斯核密度估计图，默认为True
• fit：传入scipy.stats中的分布类型，用于在观察变量上抽取相关统计特征来强行拟合指定的分布，默认为None，即不进行拟合

图中的Johnson SU为约翰逊分布，是一种经过约翰变换后服从正态分布概率的随机变量的概率分布；normal为正态分布；lognormal为对数正态分布。 通过结果我们可以看到，价格不服从正态分布，所以在进行回归之前，它必须进行转换（为什么做回归分析需要满足正态分布？？）。虽然对数变换做得很好，但最佳拟合是无界约翰逊分布(经约翰变换后服从正态分布的随机变量的概率分布)

#查看skewness（偏度） and kurtosis（峰度）
sns.distplot(Train_data['price']);
print("Skewness: %f" % Train_data['price'].skew())
print("Kurtosis: %f" % Train_data['price'].kurt())

在这里计算了price的skewness（偏度） 和 kurtosis（峰度）

• 偏度（skewness） 也称为偏态、偏态系数，是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。
• 峰度（Kurtosis） 与偏度类似，是描述总体中所有取值分布形态陡缓程度的统计量。这个统计量需要与正态分布相比较，峰度为0表示该总体数据分布与正态分布的陡缓程度相同；峰度大于0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；峰度小于0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。

#查看Train_data的skewness（偏度） and kurtosis（峰度）
Train_data.skew(), Train_data.kurt()

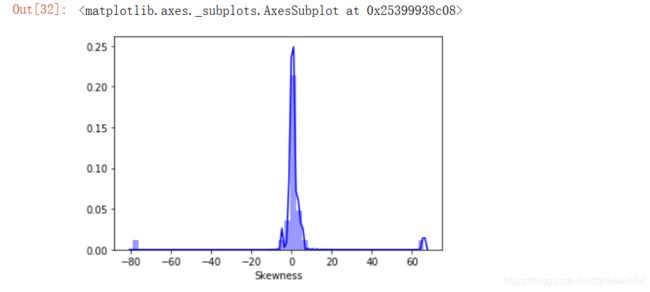
#绘制Train_data各属性的偏度
sns.distplot(Train_data.skew(),color='blue',axlabel ='Skewness')

#绘制Train_data各属性的峰度
sns.distplot(Train_data.kurt(),color='orange',axlabel ='Kurtness')

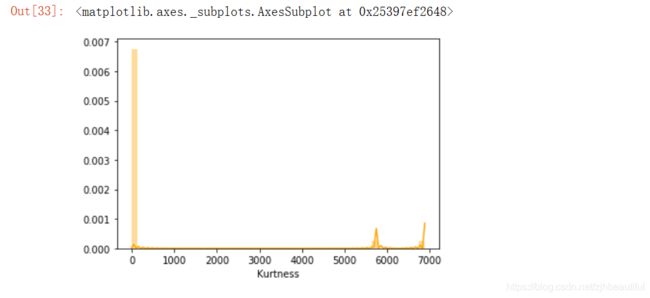
峰度Kurt代表数据分布顶的尖锐程度,偏度skew简单来说就是数据的不对称程度。skew、kurt说明参考数据的偏度和峰度——df.skew()、df.kurt()

#查看price的具体频数
plt.hist(Train_data['price'], orientation = 'vertical',color ='red')
plt.show()

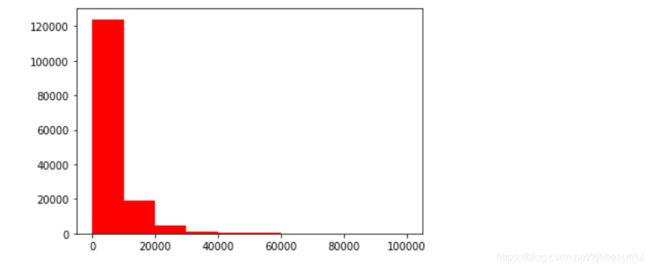
price大于20000的值极少，其实这里也可以把这些当作特殊得值（异常值）直接用填充或者删掉，在前面进行。不过直接删掉有点风险，毕竟这是个回归问题，得出的效果可能很差，需要在baseline中试一下。

# log变换 z之后的分布较均匀，可以进行log变换进行预测，这也是预测问题常用的trick
plt.hist(np.log(Train_data['price']), orientation = 'vertical',color ='red') 
plt.show()

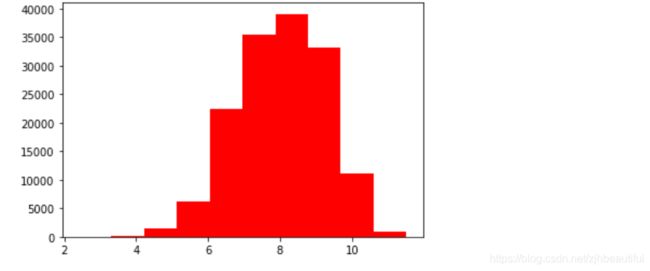
这里用log取对数变换之后的分布较为均匀，所以，可以进行log变换再进行预测，这是预测问题常用的小技巧！

2.6 特征分为类别特征和数字特征，并对类别特征查看unique分布

name - 汽车编码
regDate - 汽车注册时间
model - 车型编码
brand - 品牌
bodyType - 车身类型
fuelType - 燃油类型
gearbox - 变速箱
power - 汽车功率
kilometer - 汽车行驶公里
notRepairedDamage - 汽车有尚未修复的损坏
regionCode - 看车地区编码
seller - 销售方 【已删】
offerType - 报价类型 【已删】
creatDate - 广告发布时间
price - 汽车价格
v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14'【匿名特征，包含v0-14在内15个匿名特征】

• 分离price预测值

Y_train = Train_data['price']

• 人为（手动）区分数字变量和分类变量
  在初步观察数据字段含义时，就应该留意字段中的数字变量和类别变量，通过观测每一个字段的含义和具体数据的字段类型信息去均衡。 这里之所以不用下面注释掉的那种方式，是因为这里的类别字段都类似LabelEncoder的处理了，虽然是0,1这种类别，但都已经成了数值型，所以我们需要人为设定把它们分出来。
  • LableEncoder是将类别数据数字化的方法，使用0到n_classes-1之间的值对目标标签进行编码；
  • OneHotEncoder也是类别数据数字化的方法，可以把数据分成多个不同的列，但每一列都用0或1来表示。

# 这个区别方式适用于没有直接label coding的数据
# 这里不适用，需要人为根据实际含义来区分
# 数字特征
# numeric_features = Train_data.select_dtypes(include=[np.number])
# numeric_features.columns
# # 类型特征
# categorical_features = Train_data.select_dtypes(include=[np.object])
# categorical_features.columns

#人为设定
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]

#这里去掉了日期变量
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode',]

• 接下来对Train_data和Test_data中的类别特征进行统计

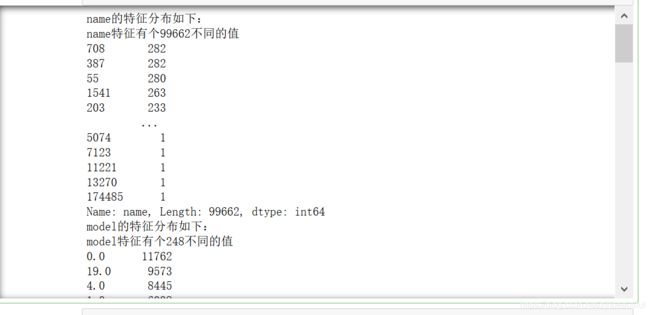
# Train_data特征nunique分布
for cat_fea in categorical_features:
    print(cat_fea + "的特征分布如下：")
    print("{}特征有个{}不同的值".format(cat_fea, Train_data[cat_fea].nunique()))
    print(Train_data[cat_fea].value_counts())

# Test_data特征nunique分布
for cat_fea in categorical_features:
    print(cat_fea + "的特征分布如下：")
    print("{}特征有个{}不同的值".format(cat_fea, Test_data[cat_fea].nunique()))
    print(Test_data[cat_fea].value_counts())

2.7 数字特征分析

#把price加入数字特征列表中
numeric_features.append('price')

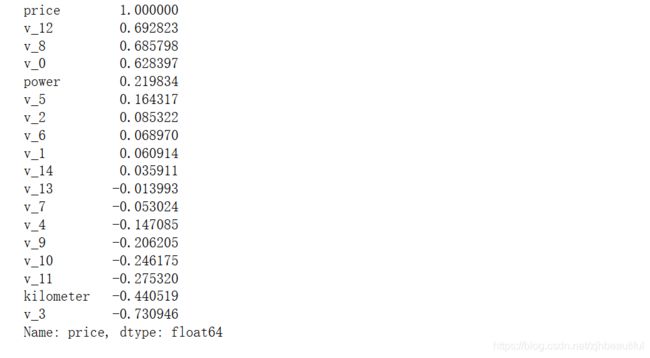
• 计算各属性与price的相关性

#相关性分析
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
#对相关性矩阵中的price列进行降序排序
print(correlation['price'].sort_values(ascending = False),'\n') 

• 绘制相关性的热力图
  使用了heatmap()函数；square=True设置为正方形；vmax, vmin为热力图颜色取值的最大值，最小值

f,ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True,vmax=0.8)

#在计算完相关性后将数字特征中的price删除
del price_numeric['price']

• 计算特征值的偏度和峰度

#查看几个特征得 偏度和峰值
for col in numeric_features:
    print('{:15}'.format(col), #字符宽度为15
          'Skewness: {:05.2f}'.format(Train_data[col].skew()) , #字符宽度为5，并保留两位小数
          '   ' ,
          'Kurtosis: {:06.2f}'.format(Train_data[col].kurt())  #字符宽度为6，并保留两位小数
         )

• 每个数字特征的分布可视化
  • 使用melt()函数将列名转换成列数据，这是个转换函数，可参考Pandas_规整数据_转换数据_melt()
  • 再使用FaceGrid和map绘制出每个属性的分布图

#每个数字特征得分布可视化
f = pd.melt(Train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=5, sharex=False, sharey=False)
g = g.map(sns.distplot, "value")

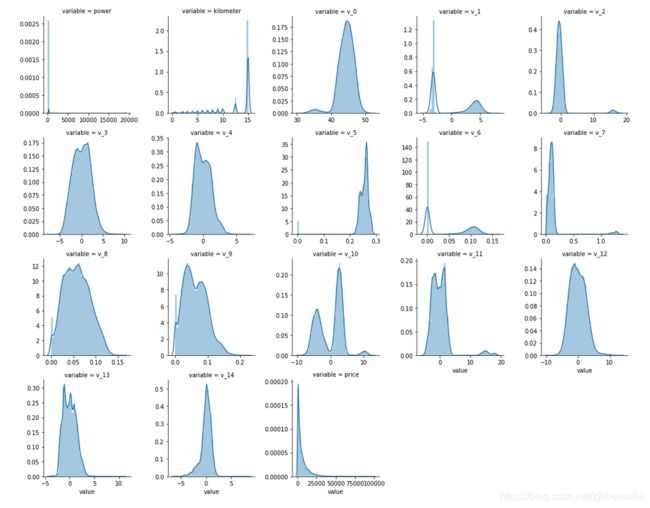
从这里可以看到数值特征的分布情况，可以看出匿名特征相对分布均匀

• 使用paiplot展示两两属性之间的关系

#每个数字特征得分布可视化
#数字特征相互之间的关系可视化
sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5',  'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()

• 多变量互相回归关系可视化
  可视化更多学习可参考很不错的文章Seaborn-05-Pairplot多变量图

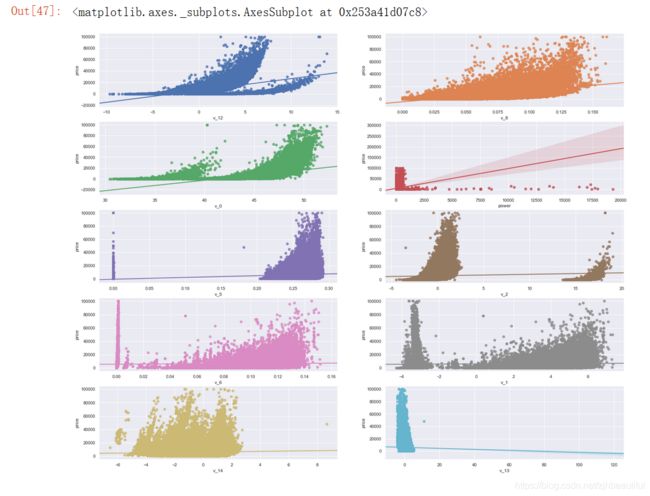
#多变量互相回归关系可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
# ['v_12', 'v_8' , 'v_0', 'power', 'v_5',  'v_2', 'v_6', 'v_1', 'v_14']
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis = 1)
sns.regplot(x='v_12',y = 'price', data = v_12_scatter_plot,scatter= True, fit_reg=True, ax=ax1)

v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)

v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)

power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)

v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)

v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)

v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)

v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)

v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)

v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)

2.8 类型特征分析

categorical_features

#unique分布
for fea in categorical_features:
    print(Train_data[fea].nunique())

从上面可以看出，name和regionCode的类别太稀疏了，所以先去掉，因为后面要可视化，不画稀疏的

• 接下来进行类别特征的各种可视化技巧
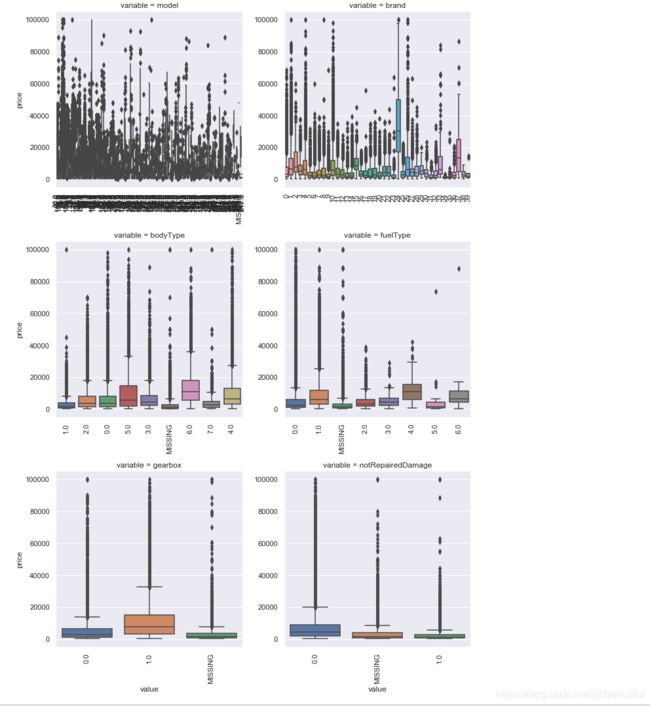
  • 类别特征箱形图可视化

#类别特征箱形图可视化

# 因为 name和 regionCode的类别太稀疏了，这里我们把不稀疏的几类画一下
categorical_features = ['model',
 'brand',
 'bodyType',
 'fuelType',
 'gearbox',
 'notRepairedDamage']
for c in categorical_features:
    Train_data[c] = Train_data[c].astype('category')
    if Train_data[c].isnull().any():
        Train_data[c] = Train_data[c].cat.add_categories(['MISSING'])
        Train_data[c] = Train_data[c].fillna('MISSING')

def boxplot(x, y, **kwargs):
    sns.boxplot(x=x, y=y)
    x=plt.xticks(rotation=90)

f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(boxplot, "value", "price")

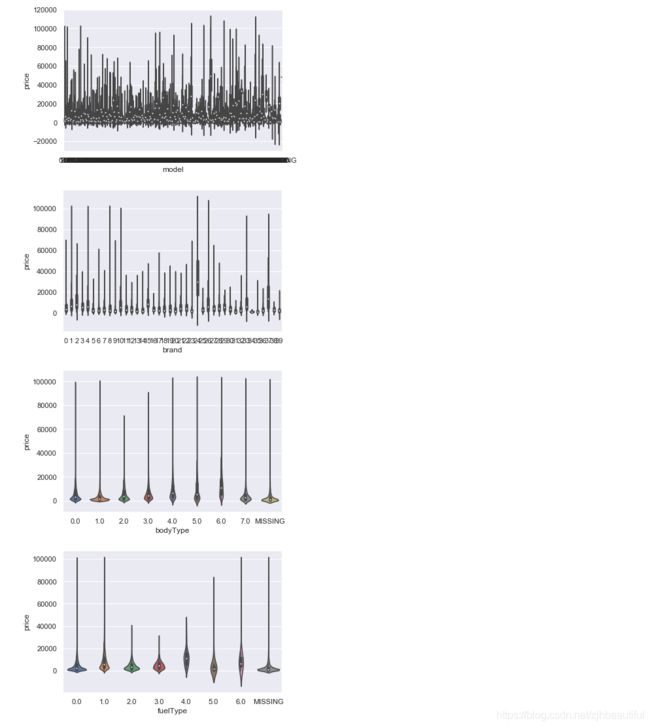
#类别特征的小提琴图可视化 
catg_list = categorical_features 
target = 'price' 
for catg in catg_list :
    sns.violinplot(x=catg, y=target, data=Train_data)
    plt.show()

1. 白点代表中位数Q2（即数据中有一半大于中位数，在其之上，另一半小于中位数，在其之下）；
2. 黑色矩形是下四分位数到上四分位数的范围，矩形上边缘为上四分位数Q3，代表数据中有四分之一的数目大于上四分位数，下边缘为下四分位数Q1，代表数据中有四分之一的数目小于下四分位数；四分位间距IQR（上四分位数和下四分为数间距）长短代表非异常数据的分散和对称程度，长则分散，短则集中；
3. 上下贯穿小提琴图的黑线代表最小非异常值min到最大非异常值max的区间，线上下端分别代表上限和下限，超出此范围为异常数据 ；
4. 黑色矩形外部形状为核密度估计，图形纵轴方向长度代表数据弥散程度，横轴方向长度代表在某纵坐标位置数据分布量。

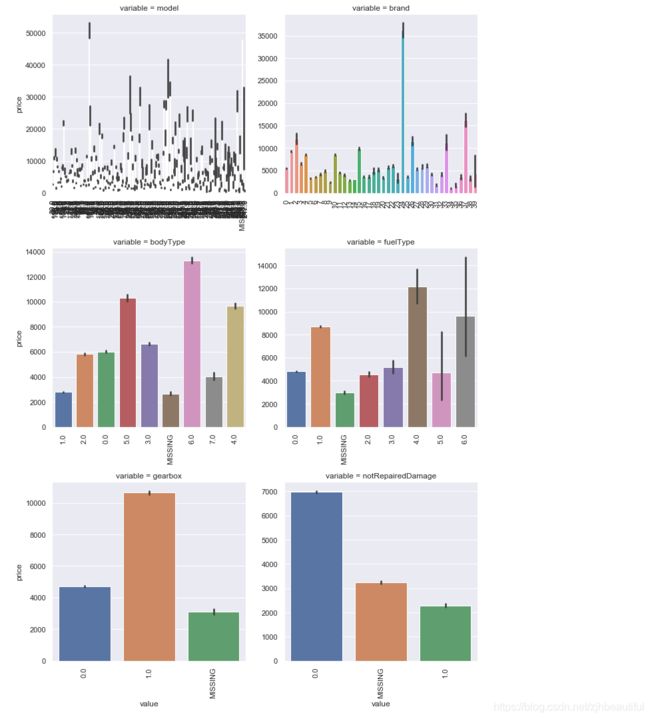
#类别特征的柱形图可视化
def bar_plot(x, y, **kwargs):
    sns.barplot(x=x, y=y)
    x=plt.xticks(rotation=90)

f = pd.melt(Train_data, id_vars=['price'], value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(bar_plot, "value", "price")

#类别特征的每个类别频数可视化(count_plot)
def count_plot(x,  **kwargs):
    sns.countplot(x=x)
    x=plt.xticks(rotation=90)

f = pd.melt(Train_data,  value_vars=categorical_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=2, sharex=False, sharey=False, size=5)
g = g.map(count_plot, "value")

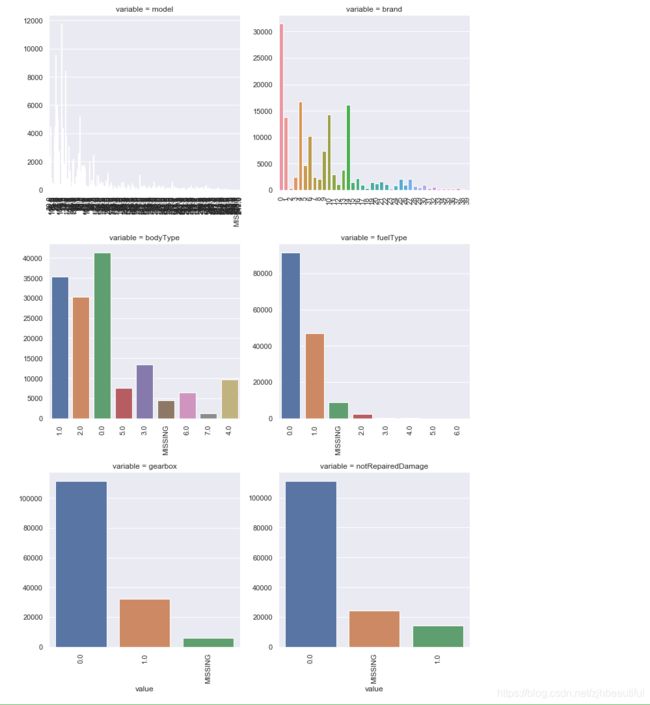
这个图还是挺好用的，可以可视化每一个类别特征的取值分布和数量，便于筛选异常

2.9 用pandas_profiling生成数据报告

pandas_profiling基于pandas的DataFrame数据类型，可以简单快速地进行探索性数据分析，使用函数ProfileReport生成一份数据探索性报告。

对于数据集的每一列，pandas_profiling会提供以下统计信息：

1、概要：数据类型，唯一值，缺失值，内存大小
2、分位数统计：最小值、最大值、中位数、Q1、Q3、最大值，值域，四分位

3、描述性统计：均值、众数、标准差、绝对中位差、变异系数、峰值、偏度系数

4、最频繁出现的值，直方图/柱状图

5、相关性分析可视化：突出强相关的变量，Spearman, Pearson矩阵相关性色阶图

并且这个报告可以导出为HTML，非常方便查看。

import pandas_profiling
pfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")

3 总结

以下总结来自Datawhale团队车哥：

• 所给出的EDA步骤为广为普遍的步骤，在实际的不管是工程还是比赛过程中，这只是最开始的一步，也是最基本的一步。接下来一般要结合模型的效果以及特征工程等来分析数据的实际建模情况，根据自己的一些理解，查阅文献，对实际问题做出判断和深入的理解。最后不断进行EDA与数据处理和挖掘，来到达更好的数据结构和分布以及较为强势相关的特征。

• 数据探索有利于我们发现数据的一些特性，数据之间的关联性，对于后续的特征构建是很有帮助的。

1. 对于数据的初步分析（直接查看数据，或.sum(), .mean()，.descirbe()等统计函数）可以从：样本数量，训练集数量，是否有时间特征，是否是时许问题，特征所表示的含义（非匿名特征），特征类型（字符类似，int，float，time），特征的缺失情况（注意缺失的在数据中的表现形式，有些是空的有些是”NAN”符号等），特征的均值方差情况。
2. 分析记录某些特征值缺失占比30%以上样本的缺失处理，有助于后续的模型验证和调节，分析特征应该是填充（填充方式是什么，均值填充，0填充，众数填充等），还是舍去，还是先做样本分类用不同的特征模型去预测。
3. 对于异常值做专门的分析，分析特征异常的label是否为异常值（或者偏离均值较远或者事特殊符号）,异常值是否应该剔除，还是用正常值填充，是记录异常，还是机器本身异常等。
4. 对于Label做专门的分析，分析标签的分布情况等。
5. 进步分析可以通过对特征作图，特征和label联合做图（统计图，离散图），直观了解特征的分布情况，通过这一步也可以发现数据之中的一些异常值等，通过箱型图分析一些特征值的偏离情况，对于特征和特征联合作图，对于特征和label联合作图，分析其中的一些关联性。