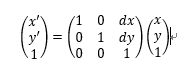AxeSlide软件项目梳理 canvas绘图系列知识点整理
默认坐标系与当前坐标系
canvas中的坐标是从左上角开始的,x轴沿着水平方向(按像素)向右延伸,y轴沿垂直方向向下延伸。左上角坐标为x=0,y=0的点称作原点。在默认坐标系中,每一个点的坐标都是直接映射到一个CSS像素上。
但是如果图像的每次绘制都参考一个固定点将缺少灵活性,于是在canvas中引入“当前坐标系”的概念,所谓“当前坐标系”即指图像在此时绘制的时候所参考的坐标系,它也会作为图像状态的一部分。比如rotate旋转操作,改变当前坐标系也就是改变了rotate的参考点,试想下如果没有当前坐标系的概念,无论是旋转,缩放,倾斜等操作不就只能参考画布左上角原点了吗。
注:以下的context均为 getContext("2d")所得的CanvasRenderingContext2D对象。
默认坐标系如下图所示:
1. 如果调用context.translate(100,50),当前坐标系与默认坐标系相对位置如下图
2. 如果调用context.scale(2,2),当前坐标系与原默认坐标系的刻度如下,红色代表当前坐标系
3. 如果调用context.rotate(Math.PI/6)顺时针旋转30度,当前坐标系与默认坐标系相对位置如下图
矩阵变换transform
上文提到的坐标变形的三种方式,平移translate,缩放scale以及旋转rotate都可以通过transform做到。
现在我们先来看看矩阵变换的定义:Context.transform(m11,m12,m21,m22,dx,dy),该方法使用一个新的变化矩阵与当前变换矩阵进行乘法运算。
| m11 | m21 | dx |
| m12 | m22 | dy |
| 0 | 0 | 1 |
也就是说假设A(x,y)要变换成B(x’,y’)可以通过乘以上述矩阵即可得到。
1 平移context.translate(dx,dy)
x’=x+dx
y’=y+dy
可以使用context.transform (1,0,0,1,dx,dy)代替context.translate(dx,dy)。
也可以使用context.transform(0,1,1,0.dx,dy)代替。
2 缩放context.scale(sx, sy)
x’=sx*x
y’=sy*y
(其中,sx 和sy分别表示在x轴和y轴上的缩放倍数)
可以使用context.transform(sx,0,0,sy,0,0)代替context.scale(sx, sy);
也可以使用context.transform (0,sy,sx,0, 0,0)代替;
3 旋转context.rotate(θ)
x’=x*cosθ-y*sinθ
y’=x*sinθ+y*cosθ
可以用context.transform(Math.cos(θ*Math.PI/180),Math.sin(θ*Math.PI/180),-Math.sin(θ*Math.PI/180),Math.cos(θ*Math.PI/180),0,0)替代context.rotate(θ)。
也可以使用context.transform(-Math.sin(θ*Math.PI/180),Math.cos(θ*Math.PI/180),Math.cos(θ*Math.PI/180),Math.sin(θ*Math.PI/180), 0,0)替代。