5/29 AprioriAll算法研究(1)
终于有时间来研究这个算法了。上上次说到这个算法非常适合学习路径的挖掘,为什么呢?因为这是一种频繁序列挖掘,与通常的频繁模式挖掘不同,它考虑到了事件出现的序列,这是非常适合学习路径的特点的,有点类似于先导课和后延课的感觉。
举个栗子:某华辑同学在某段时间学习了离散数学课程,接下来又学习了数据结构课程,那我们接下来应该给他推荐什么课呢?如果数据库里显示,学过这两门课的同学还学过Java编程语言和数据库原理两门课,那么我们应该推荐哪一门呢?可能这两门课和华辑同学学的两门课的关联程度不相上下,但是熟悉计算机或者软件专业教学安排的同学可能有一些模糊的感觉,Java编程语言看起来是更基础的课程,而数据库结构更像是学会了数据结构之后应该学的东西。没错,这就是一种序列模式,当我们匹配到频繁序列之后,我们就可以推荐之后的事件,而不是关联度同样高的之前事件了。
在AprioriAll之前先说一下Apriori思想:如果某个项集是频繁的,那么它的所有子集也是频繁的。这一思想用到关联模式发掘中就是非常成功的Apriori算法,可以快速的找到频繁项集。这一算法的详细解释一搜就有好多,这里不再赘述了。
AprioriAll本质上是Apriori思想的扩张,只是在产生候选序列和频繁序列方面考虑序列元素有序的特点,将项集的处理改为序列的处理。
基于水平格式的Apriori类算法将序列模式挖掘过程分为5个具体阶段,即排序阶段、找频繁项集阶段、转换阶段、产生频繁序列阶段以及最大化阶段。AprioriAll也是如此:
1) 排序阶段。数据库D以客户号为主键,交易时间为次键进行排序。这个阶段将原来的事务数据库转换成由客户序列组成的数据库。
2) 频繁项集阶段。找出所有频繁项集组成的集合L。也同步得到所有频繁1-序列组成的集合。
3) 转换阶段。在找序列模式的过程中,要不断地进行检测一个给定的频繁集是否包含于一个客户序列中。
4) 序列阶段。利用已知的频繁集的集合来找到所需的序列。类似于关联的Apriori算法。
5)最大化阶段。在频繁序列模式集合中持出最大频繁序列模式集合
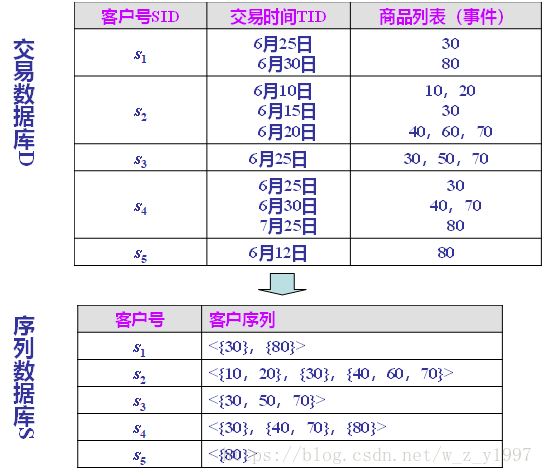
1.排序阶段
对原始数据表(交易数据库D)按客户号(作为主关键字)和交易时间(作为次关键字)进行排序,排序后通过对同一客户的事件进行合并得到对应的序列数据库(序列数据库S)。
2.找频繁项集阶段
这个阶段根据min_sup找出所有的频繁项集,也同步得到所有频繁1-序列组成的集合L1,因为这个集合正好是{
例:
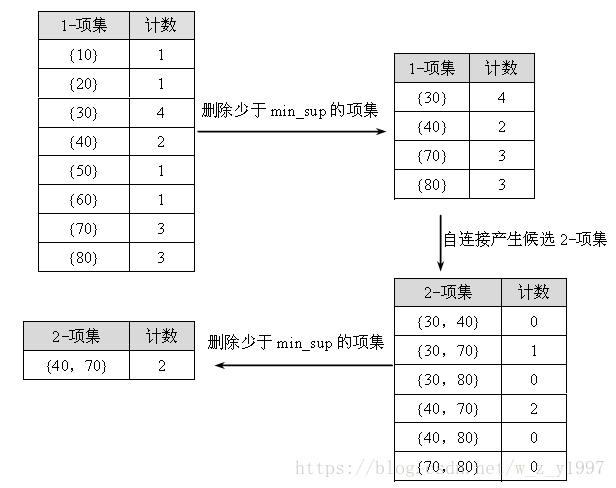
对于刚才的序列数据库S,假设min_sup=2。找频繁项集的过程如下:
最后求得的频繁1-序列L1={{30},{40},{70},{40,70},{80}}。
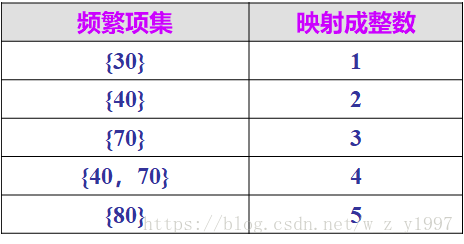
然后将频繁1-项集映射成连续的整数。例如,将上面得到的L1映射成表6.4对应的整数。由于比较频繁项集花费一定时间,这样做后可以减少检查一个序列是否被包含于一个客户序列中的时间,从而使处理过程方便且高效。
3.转换阶段
在寻找序列模式的过程中,要不断地进行检测一个给定的大序列集合是否包含于一个客户序列中。为此做这样的转换:
- 每个事件被包含于该事件中所有频繁项集替换。
- 如果一个事件不包含任何频繁项集,则将其删除。
- 如果一个客户序列不包含任何频繁项集,则将该序列删除。
这样转换后,一个客户序列由一个频繁项集组成的集合所取代。每个频繁项集的集合表示为{e1,e2,…,ek},其中ei(1≤i≤k)表示一个频繁项集。
之前的序列数据库S经过转换后的结果类似这样:
4.产生频繁序列阶段
利用转换后的序列数据库寻找频繁序列,AprioriAll算法如下:
输入:转换后的序列数据库S,所有项集合I,
最小支持度阈值min_sup
输出:序列模式集合L
方法:其过程描述如下:
其中,利用频繁序列Lk-1生成候选k-序列Ck的过程说明如下:(csdn的下角标不会打 大家将就着看吧)
(1)链接
对于Lk-1中任意两个序列s1和s2,如果s1与s2的前k-2项相同,即s1=
(2)剪枝
剪枝的原则:一个候选k-序列,如果它的(k-1)-序列有一个是非频繁的,则删除它。由Ck剪枝产生Lk的过程如下:
例:某序列数据库S1经过转换后,给出ApriorAll算法的执行过程,这里I={1,2,3,4,5},每个数字表示一个项。假设min_sup=2。(与前例无关)
序列数据库S2
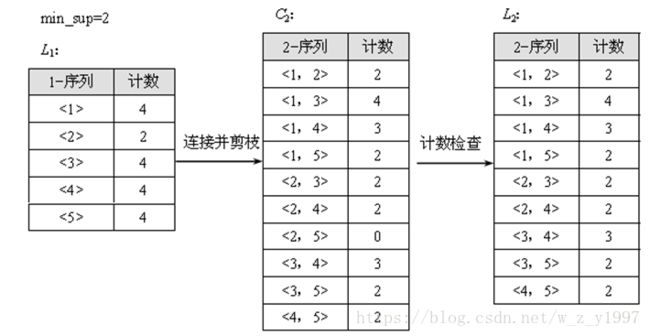
① 先求出L1,由其产生L2的过程如图6.2所示,实际上这个过程不需要剪枝,因为C2中每个2-序列的所有子序列一定属于L1。
产生L2的过程
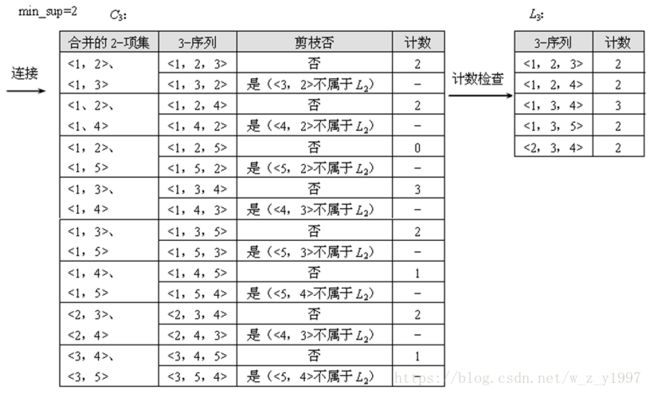
② 由L2连接并剪枝产生C3,扫描序列数据库S1,删除小于min_sup的序列得到L3,其过程如下所示。
产生L3的过程
③ 由L3连接并剪枝产生C4,扫描序列数据库S1,删除小于min_sup的序列得到L4,其过程如下所示。
产生L4的过程
④ L4中只有一个序列,由它产生的C5为空,L5也为空。算法结束。
5.最大化阶段
在频繁序列模式集合中持出最大频繁序列模式集合。
由于在产生频繁模式阶段发现了所有频繁模式集合L,下面的过程可用来发现最大序列。设最长序列的长度为n,则:
例:对于前面的序列数据库S2,从前面的过程看到,产生的所有频繁序列集合:
L={<1>,<2>,<3>,<4>,<5>,<1,2>,<1,3>,<1,4>,<1,5>,<2,3>,<2,4>,<3,4>,<3,5>,<4,5>,<1,2,3>,<1,2,4>,<1,3,4>,<1,3,5>,<2,3,4>,<1,2,3,4>}
删除子序列得到最大序列的过程如下:
由于最长的序列是4,因此所有4-序列都是最大序列,这里只有<1,2,3,4>是最大序列。
对于4-序列<1,2,3,4>,从L中删除它的3-子序列<1,2,3>、<1,2,4>、<1,3,4>、<2,3,4>,2-子序列<1,2>、<1,3>、<1,4>、<2,3>、<2,4>、<3,4>和1-子序列<1>、<2>、<3>、<4>,剩下的3-序列<1,3,5>是最大序列。
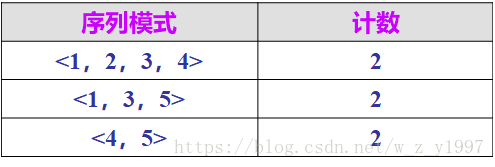
对于3-序列<1,3,5>,从L中删除它的2-子序列<1,5>、<3,5>和1-子序列<5>,剩下的2-序列<4,5>是最大序列。
到此,L中已没有可以再删除的子序列了,得到的序列模式如下表所示。
到此为止,AprioriAll算法就得到了频繁序列。