20191126 B+tree数据结构
查询速度更快,查询更稳定。
关键字:索引字段的值信息,左闭合区间原则。
二叉树
数据结构中的二叉树;树是一种一对多的数据结构。树又有很多子集,比如:二叉树、二叉搜索树、2-3树、红黑树等等。
树的特征:
1.没有父结点的结点叫根(根结点),一个数有且只有一个根;
2.每个结点有0个或多个子结点;
3.一颗树里也可拥有子树,且子树不能相交;
(根结点,子结点,叶子结点,子树)
度
每个结点拥有的子树数量称为该结点的度(直接子节点,不能间接),简单的说结点的子节点个数就是它的度。例如上图中D结点的度为3。度为0的结点成为叶节点,也就是没有子结点的结点`。
二叉树
二叉树的特征:
1.每个结点最多有2个子结点的树(就是不存在度大于2的结点);
2.左右子树有一定顺序(比如升序或降序,如下图中8的右子结点大于左子节点,结点2和7的子节点也是如此关系)。(左右子结点之间有一定的顺序关系,左侧的小于右侧的)
二叉树:简单地理解,满足以下两个条件的树就是二叉树:本身是有序树;树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二叉树具有以下几个性质:
1、二叉树中,第 i 层最多有 2i-1 个结点。
2、如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
满二叉树
满二叉树是所有非叶结点的子结点个数都为2,看起来呈水平对称。其特征为:
1.所有叶结点都在最后一层;
2.非叶结点的所有结点的度都为2;
二叉树的顺序存储结构
二叉树的存储结构有两种,分别为顺序存储和链式存储。本节先介绍二叉树的顺序存储结构。
采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。
采用链式存储二叉树时,其节点结构由 3 部分构成(如下图所示):
1、指向左孩子节点的指针(Lchild); 数据域+指针。
2、节点存储的数据(data);
3、指向右孩子节点的指针(Rchild);
二叉树先序遍历
二叉树先序遍历的实现思想是:
- 访问根节点;
- 访问当前节点的左子树;
- 若当前节点无左子树,则访问当前节点的右子树;
前序遍历,也叫先根遍历,遍历的顺序是,根,左子树,右子树
遍历结果:A,B,E,F,C,G
中序遍历,也叫中根遍历,顺序是 左子树,根,右子树
遍历结果:E,B,F,A,G,C
后序遍历,也叫后根遍历,遍历顺序,左子树,右子树,根
遍历结果:E,F,B,G,C,A
平衡二叉树
B Tree指的是平衡树,平衡二叉树是基于二分法的策略提高数据的查找速度的二叉树的数据结构。
平衡二叉树是采用二分法思维把数据按规则组装成一个树形结构的数据,用这个树形结构的数据减少无关数据的检索,大大的提升了数据检索的速度;
非叶子节点只能允许最多两个子节点存在,每一个非叶子节点数据分布规则为左边的子节点小当前节点的值,右边的子节点大于当前节点的值(这里值是基于自己的算法规则而定的,比如hash值);
子结点,根结点,子结点。 最后一个结点为叶子结点。
1)左侧的子节点小于当前结点的值;
2)右侧的子节点大于当前结点的值。
保证数据平衡的情况下查找数据的速度近于二分法查找;
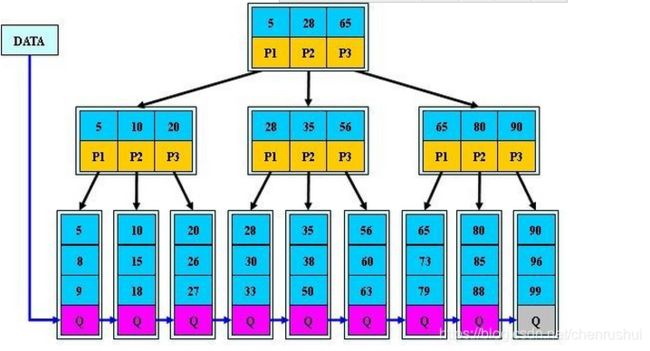
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。
1、B+树的非叶子节点不保存关键字记录的指针,这样使得B+树每个节点所能保存的关键字大大增加;子节点不保存指针。
2、B+树叶子节点保存了父节点的所有关键字和关键字记录的指针,每个叶子节点的关键字从小到大排列;
3、B+树的根节点关键字数量和其子节点个数相等;
4、B+的非叶子节点只进行数据索引,不会存实际的关键字记录的指针,所有数据地址必须要到叶子节点才能获取到,所以每次数据查询的次数都一样;
5、在B树的基础上每个节点存储的关键字数更多,树的层级更少所以查询数据更快,所有指关键字指针都存在叶子节点,所以每次查找的次数都相同所以查询速度更稳定;
explain select id from p_hospital where id<10 范围查找会走索引。
树形结构是计算机系统里最重要的数据结构。
B+树是B树的变种,它在每个子节点里都只存放关键字信息,而只在叶子节点中存放存储所需的其它附属信息,这样就可以让子节点的分支因子最大化,也让树的高度尽可能的低。
子结点,叶子结点,降低树的高度。
B+树的创造者 Rudolf Bayer 没有解释B代表什么。最常见的观点是B代表平衡(balanced)。
B树,平衡树,平衡二叉树。
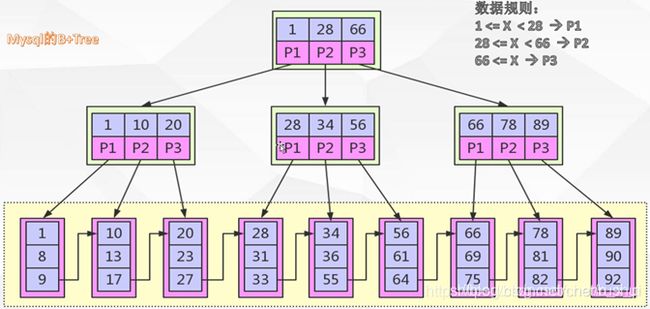
B+TREE中,数据检索规则采用的是左闭合区间,路数和关键个数关系为1比1,具体如下图所示:
B TREE和B+TREE区别是什么?
1、B+TREE 关键字的搜索采用的是左闭合区间,之所以采用左闭合区间是因为他要最好的去支持自增id,这也是mysql的设计初衷。即,如果id = 1命中,会继续往下查找,直到找到叶子节点中的1。
2、B+TREE 根节点和支节点没有数据区,关键字对应的数据只保存在叶子节点中。即只有叶子节点中的关键字数据区才会保存真正的数据内容或者是内容的地址。
MYSQL为什么最终要去选择B+TREE?
1、B+TREE是B TREE的变种,B TREE能解决的问题,B+TREE也能够解决(降低树的高度,增大节点存储数据量)
2、B+TREE扫库和扫表能力更强,如果我们要根据索引去进行数据表的扫描,对B TREE进行扫描,需要把整棵树遍历一遍,而B+TREE只需要遍历他的所有叶子节点即可(叶子节点之间有引用)。
3、B+TREE磁盘读写能力更强,他的根节点和支节点不保存数据区,所有根节点和支节点同样大小的情况下,保存的关键字要比B TREE要多。而叶子节点不保存子节点引用。所以,B+TREE读写一次磁盘加载的关键字比B TREE更多。
4、B+TREE排序能力更强,如上面的图中可以看出,B+TREE天然具有排序功能。
5、B+TREE查询效率更加稳定,每次查询数据,查询IO次数一定是稳定的。当然这个每个人的理解都不同,因为在B TREE如果根节点命中直接返回,确实效率更高。
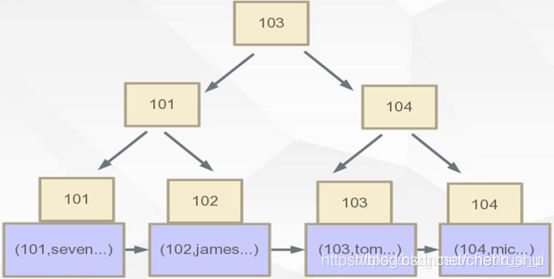
数据以主键进行聚集存储,把真正的数据保存在叶子节点中。innodb设计初衷认为主键才是最主要的索引。
如上图中,叶子节点的数据区保存的就是真实的数据,在通过索引进行检索的时候,命中叶子节点,就可以直接从叶子节点中取出行数据。
主键索引的叶子节点保存的是真正的数据。而辅助索引叶子节点的数据区保存的是主键索引关键字的值。
搜索过程为:假如要查询name = seven的数据,先在辅助索引中查询最后找到主键id = 101,再在主键索引中搜索id为101的数据,最终在主键索引的叶子节点中获取到真正的数据。所以通过辅助索引进行检索,需要检索两次索引。