python聚类分析实现电商用户细分（基于RFM用户价值分析模型）

背景

聚类分析在机器学习领域属于无监督学习的一种，能够根据一些特征对样本数据进行分类。使用聚类分析分完的类具有“类中相似，类间区别”的特点。RFM模型是非常常见的分析用户价值的方法，其核心思想是根据用户的最近购买时间、购买频次、花费金额3个特征来对用户进行分群，针对每个群体采取不同的营销手段。k-means是常用的聚类分析算法之一，基于欧氏距离对样本进行分类。k-means算法运行速度快，能够处理的数据量大，且易于理解。但缺点也很明显，就是算法性能有限，在高维上可能不是最佳选项。在当前动辄上亿的数据量来看，k-means算法是比较好的选择了。还有需要提醒的一点是，一定要结合业务使用算法，任何特征都可能拿来聚类，但是聚类的结果呢，能不能很好的解释和指导业务？如果不能，那么这个算法就没有什么意义。本次使用的数据来源于数据不吹牛公众号，这里也是小打一波广告。
本案例将从一个简单的k-means机器学习模型入手，在介绍聚类算法的同时也简单介绍机器学习的常规步骤。

1、数据概览

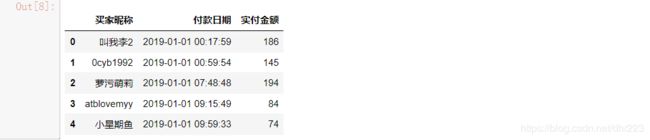
首先，我们导入数据，并查看前5行。

import pandas as pd
import numpy as np
df = pd.read_excel(r'F:\数据分析项目\电商数据的RFM模型\RFM\PYTHON-RFM实战数据.xlsx')
df.head(5)

总览数据：

df.info()

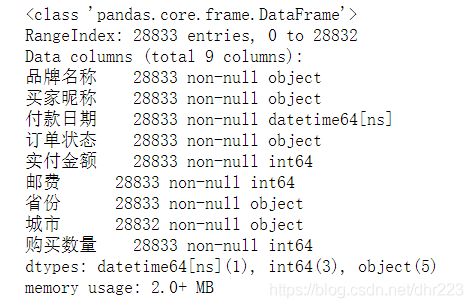
数据共有28833行，9列，而且数据非常干净，没有空值，省去了我们处理空值的过程。
根据RFM模型的要求，我们需要的是买家昵称、购买日期、实付金额三个变量。其中购买日期和实付金额用于帮助我们训练模型，买家昵称则让我们确定每个用户所属的类别。

选取交易成功的用户：

df['订单状态'].value_counts()
df = df[df['订单状态'] == '交易成功']

选择我们需要的字段：

data = df[['买家昵称', '付款日期',  '实付金额']]
data.head(5)

有个细节需要注意，订单每一行代表着单个用户的单次购买行为，什么意思呢？如果一个用户在一天内购买了4次，订单表对应记录着4行，而在实际的业务场景中，一个用户在一天内的多次消费行为，应该从整体上看作一次。 ----- 数据不吹牛 小Z

2、特征构建

根据我们的RFM模型，我们需要构建3列数据，这个原始表中是没有直接提供的，需要我们根据原始表的数据来提取。
所以这里需要先提取付款日期数据：

data['paytime'] = pd.to_datetime(data['付款日期'].apply(lambda x:x.date()))
data.head()

根据paytime计算最后一次付款时间距当前的天数（数据引用的背景当前时间是2019-07-01）：

# 提取每个用户最近（最大）的购买日期
data_r = data.groupby('买家昵称')['paytime'].max().reset_index()
# 与当前日期相减，取得最近一次购买距当前的天数。
data_r['recency'] = data_r['paytime'].apply(lambda x:(pd.to_datetime('2019-07-01')-x).days)
# 两个日期相减，得到的数据类型是timedelta类型，要进行数值计算，需要提取出天数数字。
data_r.drop('paytime',axis = 1,inplace = True)
data_r.head()

提取购买次数数据：

# 分组聚合，得到每个用户发生于不同日期的购买次数
data_f = data.groupby(['买家昵称','paytime'])['付款日期'].count().reset_index()
data_f = data_f.groupby('买家昵称')['paytime'].count().reset_index()
# 修改列名
data_f.rename({'paytime':'frequence'},axis = 1,inplace = True)
data_f.head()

提取购买金额数据，这里的金额我们使用每个用户的金额/次：

data_m = data.groupby('买家昵称')['实付金额'].sum().reset_index()
data_m['money'] = data_m['实付金额']/data_f['frequence']
data_m.drop('实付金额',axis = 1,inplace = True)
data_m.head()

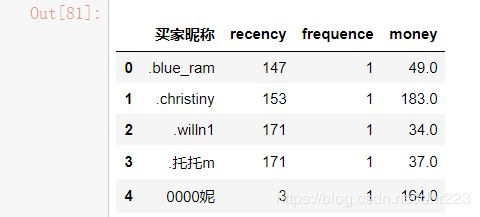
所以现在我们已经有了包含recency、frequence、money的3个DataFrame表了，下面合并三个表：

data_rf = pd.merge(data_r,data_f,on = '买家昵称',how = 'inner')
data_rfm = pd.merge(data_rf,data_m, on = '买家昵称',how = 'inner')
data_rfm.head()

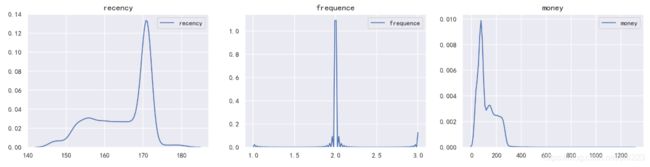
3、查看数据分布特征

数据的分布特征会影响算法结果，所以有必要先了解数据的大致分布。

import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize = (6,4))
sns.set(style = 'darkgrid')
sns.countplot(data_rfm['frequence'])

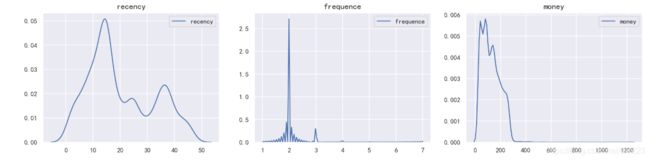
sns.distplot(data_rfm['recency'])
plt.title('recency的分布直方图',fontsize = 15)

sns.distplot(data_rfm['money'],color = 'g')
plt.title('money的分布直方图',fontsize = 15)

4、数据处理及模型构造

首先，对数据进行标准化处理，这是为了消除量纲的影响。

from sklearn import preprocessing
from sklearn.cluster import KMeans
from sklearn import metrics
data_rfm_s = data_rfm.copy()
min_max_scaler = preprocessing.MinMaxScaler()
data_rfm_s = min_max_scaler.fit_transform(data_rfm[['recency','frequence','money']])

K-Means方法有个经常被人诟病的地方，如何选择K值？也就是要把样本分成多少类呢？如果贸然定一个，会太主观，所以还是要用数据说话。一般采用三个指标：

• Calinski-Harabaz Index。通过计算类中各点与类中心的距离平方和来度量类内的紧密度，通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度，CH指标由分离度与紧密度的比值得到。从而，CH越大代表着类自身越紧密，类与类之间越分散，即更优的聚类结果。
• 轮廓系数。轮廓系数（Silhouette Coefficient），值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优。也就是尽量选择更大的轮廓系数。
• inertia值。kmeans自带的评价方法，越小说明聚类效果越好。

inertia = []
ch_score = []
ss_score = []
for k in range(2,9):
    model = KMeans(n_clusters = k, init = 'k-means++',max_iter = 500)
    model.fit(data_rfm_s)
    pre = model.predict(data_rfm_s)
    ch = metrics.calinski_harabaz_score(data_rfm_s,pre) 
    ss = metrics.silhouette_score(data_rfm_s,pre)
    inertia.append(model.inertia_)
    ch_score.append(ch)
    ss_score.append(ss)
print(ch_score,ss_score,inertia)

画图可以更加直观看出三个指标的变化：

score = pd.Series([ch_score,ss_score,inertia],index = ['ch_score','ss_score','inertia'])
aa = score.index.tolist()
plt.figure(figsize = (15,6))
j = 1
for i in aa:
    plt.subplot(1,3,j)
    plt.plot(list(range(2,9)),score[i])
    plt.xlabel('k的数目',fontsize = 13)
    plt.ylabel(f'{i}值',fontsize = 13)
    plt.title(f'{i}值变化趋势',fontsize = 15)
    j+=1
plt.subplots_adjust(wspace = 0.3)

根据上图中3个指标综合判断，选择k=4时，各指标变化出现明显的拐点，聚类效果相对较优，所以分成四类比较好。

model = KMeans(n_clusters = 4, init = 'k-means++',max_iter = 500)
model.fit(data_rfm_s)
ppre = model.predict(data_rfm_s)
ppre = pd.DataFrame(ppre)
data = pd.concat([data_rfm,ppre],axis = 1)
data.rename({0:u'cluster'},axis = 1,inplace = True)
data.head()

可以看出，每个用户都有了对应的类别，并且可以查看每个类别的中心：

labels = model.labels_   # 取得各样本的类别数据
labels = pd.DataFrame(labels,columns = ['类别'])
result = pd.concat([pd.DataFrame(model.cluster_centers_),labels['类别'].value_counts().sort_index()],axis = 1)
result.columns = ['recency','frequence','money','cluster']
result

cluster=0时的分布状态：

cluster=1时的分布状态：

cluster=2时的分布状态：

cluster=3时的分布状态：