十五、方差分析--使用Python进行单因素方差分析（ANOVA）

方差分析

方差分析（Analysis of Variance，简称ANOVA），又称为“变异数分析”， 是由英国统计学家费歇尔（Fisher）在20世纪20年代提出的，可用于推断两个或两个以上总体均值是否有差异的显著性检验。

由于各种因素的影响，研究所得的数据呈现波动性。造成波动的原因可分成两类，一是不可控的随机因素，另一是研究中施加的对结果形成影响的可控因素。

方差分析一般可以分为单因素方差分析和多因素方差分析。我们从单因素方差分析开始。

1. 单因素方差分析

所谓单因素方差分析就是只考虑一个因素对实验结果造成的影响。

1.1. 单因素方差分析的理论

设实验只有一个因素（因子）A，有r个水平$A_1,A_2,...,A_r$。现在水平$A_i$下进行$n_i$次独立观测，得到观测数据$X_{ij},i=1,2,...,r,j=1,2,...,n_i$， 得到实验指标的数据如下：

各总体间相互独立，因此有如下数学模型：
$$\{\begin{array}{l}{X}_{ij}={\mu }_i+{\epsilon }_{ij},\\ {\epsilon }_{ij}\sim N(0,{\sigma }^2),各{\epsilon }_{ij}独立，\\ i=1,2,...,r,j=1,2,...,n_i.\end{array}$$
其中的${\mu }_i$就是在第$i$个水平下的均值，${\epsilon }_{ij}$是随机误差。

方差分析的目的就是要比较因素A的r个水平下试验指标理论均值的差异，因此方差分析其本质是利用假设检验对多组数据的均值进行分析。即如下的假设检验：
$$H_0:{\mu }_1={\mu }_2=...={\mu }_r{H}_1:{\mu }_1,{\mu }_2,...,{\mu }_r不全相等$$
如果$H_0$被拒绝，则说明因素A的各个水平的效应之间有显著的差异，否则，差异不明显。

按照方差分析的思想，采用离差平方和分解，即：

• 假设数据总的差异用总离差平方和$S_T$表示
  $$S_T=\sum _{i=1}^r\sum _{j=1}^{n_i}(X_{ij}-\overline{X}{)}^2$$
• 因素A引起的差异–效应平方和$S_A$表示
  $$S_A=\sum _{i=1}^r{n}_i(\overline{X_{i.}}-\overline{X}{)}^2$$
• 随机误差所引起的差异–误差平方和$S_E$表示
  $$S_E=\sum _{i=1}^r\sum _{j=1}^{n_i}(X_{ij}-\overline{X_{i.}}{)}^2$$
  这里称$S_T$为总离差平方和（或称总变差），它是所有数据$X_{ij}$与总平均值$\overline{X}$之差的平方和，描绘所有观察数据的离散程度；$S_E$为误差平方和（组内平方和），是对固定的$i$，观测值$X_{i1},X_{i2},...,X_{i{n}_i}$之间的差异大小的度量。$S_A$为因素A的效应平方和（或组间平方和），表示因子A各水平下的样本均值和总平均值之差的平方和。

方差分析有如下定理：
(1) $S_T=S_A+S_E,$
(2) $\frac{S_E}{{\sigma }^2}\sim {\chi }^2(n-r),$
(3) $S_A与S_E相互独立,$
当$H_0$为真时，$\frac{S_A}{{\sigma }^2}\sim {\chi }^2(r-1)$， 于是由：
$$F=\frac{S_A/(r-1)}{S_E/(n-r)}\sim F(r-1,n-r)$$

方差分析计算量比较大，通常都是直接使用统计软件完成计算的。

1.2. Python单因素方差分析

使用Python进行单因素分析涉及到如下库：

• Numpy: 一个用于处理多维数组的库
• Pandas：在Python数据处理中使用最多的库
• Patsy：也公式处理库
• Statsmodels：该库包含很多统计分析模型
  建议大家安装Anaconda3，它是专门用于科学计算的一个Python环境，其中已经集成了上面涉及的几个库。

例1：为了对几个行业的服务质量进行评价，消费者协会在4个行业分别抽取了不同的企业作为样本，最近一年中消费者对总共23家企业投诉的次数如下表：

第一步：数据输入
因为后面进行分析时所采用的数据结构通常是Pandas的DataFrame，为此我们将数据首先录入一个DataFrame中，代码如下：

import pandas as pd

data = pd.DataFrame({'零售业':[57, 66, 49, 40, 34,53,44],
                     '旅游业':[68,39, 29,45, 56, 51, np.nan],
                     '航空公司':[31,49, 21,34,40, np.nan, np.nan],
                     '家电制造业':[44,51, 65, 77, 58,np.nan, np.nan]})
                    
data.columns.name='行业'

在jupyter notebook中输出data如下：

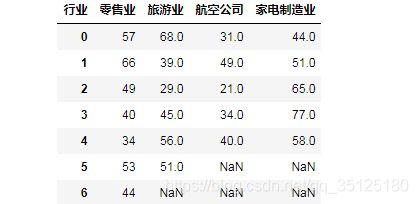
第二步：数据处理
其实上一步得到的数据框并不能满足statsmodels中模型库的要求，因此要进行数据处理，以满足相应模型的输入要求。

df1=data.melt().dropna()

上述代码首先使用数据框的melt()方法，将数据由所谓的“宽格式”转换为“长格式”，并且使用dropna()方法删除了空值。如果你对pandas的数据处理不熟悉，建议参考相关文档。

这是在jupyter notebook下输出df1如下：

第三步：使用模型进行分析
这里我们使用Python中statsmodels模型库中的相关方法进行分析。

# 导入相关库
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

model = ols('value ~ C(行业)', df1).fit()
anova_lm(model)

上述代码中ols的作用就是从一个公式和数据框创建一个模型。这里的公式语法就是由Patsy库提供支持的，C函数完成分类变量转换。
anova_lm就是为模型产生一个方差分析表。

在jupyer notebook下产生的输出如下：

这里的输出与前面“单因素实验方差分析表”形式略有不同，但是本质上是一样的。只不过这里只给出了总离差平方和及组间离差平方和，但是不要忘记知道了二者，其实组内离差平方和是可以计算的。所以本质上这个输出以及完全可以满足方差分析的要求了。

第四部：对结果进行解释和决策
在显著性水平$\alpha =0.05$下，由于p=0.038765 <$\alpha =0.05$,因此我们拒绝原假设，认为不同的行业投诉存在差异。

2. 单因素方差分析中的其他问题

在单因素方差分析中，我们基于如下的几个假设：

• 正态性：总体服从正态分布
• 方差齐性：各个总体的方差相等

方差分析对于正态性的要求不是很敏感，当然在不服从正态分布的情况可以使用非常检验了。
对于方差齐性的要求，可以使用相应的方法进行检验。

2.1. 方差齐性检验

from scipy import stats

d1=df1[df1['行业']=='零售业']['value']
d2=df1[df1['行业']=='旅游业']['value']
d3=df1[df1['行业']=='航空公司']['value']
d4=df1[df1['行业']=='家电制造业']['value']
args=[d1,d2,d3,d4]

w,p = stats.levene(*args)
w,p
# output:
(0.19727325330223064, 0.8969450951218239)

这里的输出中，第一个值为检验统计量（使用了t检验），第二个值为p值。所以在显著性水平$\alpha =0.05$下，可以认为满足方差齐性的要求。

2.2. 方差分析中的多重检验

在方差分析中，如果拒绝了原假设，只能说明均值不全相等。那么，它们中有没有部分是相等的？这就涉及到方差分析中的多重检验。

from scipy import stats

pair_t = model.t_test_pairwise("C(行业)")
pair_t.result_frame

在jupyter notebook中显示如下：

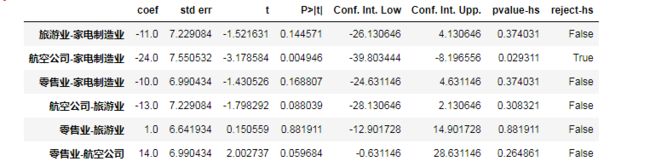
由上面的输出结果可以看出，航空公司和家电制造业的平均投诉存在较明显差异。

3. 总结

在进行方差分析学习时，其实建议大家要弄明白其原理，可以根据原理使用Python的基本库进行计算，这样其实可以加深对理论的理解。但是，在实际工作中必然是要尽量避免重复造轮子了，所以了解和掌握已有的相关库，无疑会大大提高工作的效率，接下来会通过Python实现双因素的方差分析。