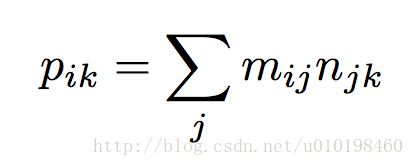spark矩阵向量-矩阵矩阵相乘
import org.apache.spark.util._
val paramatrix1 = sc.parallelize(List(Vector(2, 2, 4), Vector(3, 2, 1), Vector(1, 3, 2)))//首先,在spark shell中将一个矩阵按照行进行并行化,
val vec1 =Vector(1,2,4)//定义一个向量
val m1=paramatrix1.map(_ dot(vec1))//dot 操作将两个向量相乘,得到点积。这里需要注意的是,虽然并行操作并不保证先后顺序,但是结果是依然有先后顺序的。
//mapreduce 在做矩阵向量相乘的时候,是按照把每个元素的行作为key。每个元素的值作为value,reduce的过程是相同的key的value相加,得到结果。
spark也可以这样做,但是并没有优势,每个元素都需要并行化成一个RDD,那么m*m的矩阵就需要有m^2个task。而按行相乘,只需要m个task,在实际的应用中足够了。
如果文件超大,不能在内存中放入,那么需要对矩阵和向量进行切割。切割方式如下:
切割之后,把相应的部分乘起来即可。
2,矩阵矩阵相乘。
S=M*N。把矩阵N的每个列作为上面的一个向量。即变成了矩阵和向量相乘,然后按照上述步骤计算即可。得到的结果是一个S的一个列。但是RDD提供了一个函数cartesian可以为这种计算提供便利。cartesian可以返回两个RDD的所有组合。并且保证秩序。因此可以很方便来进行矩阵运算。
val paramatrix1 = sc.parallelize(List(Vector(2, 2, 4), Vector(3, 2, 1), Vector(1, 3, 2)))//矩阵M
val paramatrix2 = sc.parallelize(List(Vector(2, 3, 1), Vector(2, 2, 3), Vector(4, 1, 2)))//矩阵N ,the same matrix as M .只是存储的方式不一样,N是按列存储
val m2= paramatrix1.cartesian(paramatrix2)#排序次序是RDD1的第一个元素依次和RDD2的所有元素,然后是RDD1的第二个元素依次和RDD2 的所有元素。
//因此取前n个元素,构成了结果矩阵S(n*n)的第一行,(n+1)到2n个元素,构成了S的第二行
val temp=m2.map(x=>x._1.dot(x._2))//然后把每个pair里面的元素取点积.再按照上面的排序取出矩阵,就是最终的结果。
但是上述过程存在一个问题。就是中间结果的数据量将是原始矩阵的n倍。因此在大数量的时候也可以考虑矩阵向量的乘法来比较一下两者的性能。
当然,针对稀疏矩阵还可以通过对矩阵的元素按行列来索引数据。通过构建小的pair来计算矩阵相乘。
下面介绍实现思想和方法。
假设M由(i,j,v)构成,N由(j,k,w构成),其中i,j为矩阵元素的行和列索引。那么S=M*N的元素(i,k,p)的计算如下式。
从上式可以看出,(i,k,p)的计算是由M的i行和N的k列构成。由于m(ij)和n(j,k)中的j是共有元素,可以按j来构造键值。
即每个M中的元素构建为(j,(i,v))。每个N中的元素构建为(j,(k,w))。然后两个元素相乘。构造成((i,k),j,v*w)。最后按键值(i,k)相加,构成((i,k),p)。
代码如下:
首先构造两个矩阵,按元素并行化,不出现的元素即为0
val paramatrix1 = sc.parallelize(List(Vector(1, 1, 1), Vector(2, 2, 2),Vector(2, 1, 3), Vector(3, 3, 4)))//有四个元素
val paramatrix2 = sc.parallelize(List(Vector(1, 1, 5), Vector(2, 2, 6),Vector(2, 3, 7), Vector(3, 3, 8)))
val tempM = paramatrix1.map(x=>(x(1),(x(0),x(2))))//转化成(j,(i,v))
val tempN = paramatrix2.map(x=>(x(0),(x(1),x(2))))//转化成(j,(k,w))
val temp1= tempM.cartesian(tempN).filter(x=>x._1._1==x._2._1)//将具有相同j的所有i.k都聚到同一个pair中。
val temp2=temp1.map(x=>((x._1._2._1,x._2._2._1),x._1._2._2*x._2._2._2))// 重塑这个pair,使之具有((i,k),v*w)形式。
val temp3=temp2.reduceByKey(_+_)//具有相同pair的元素相加。即得到最终结果。
经测试结果正确。下面再测试一个完全没有零元素的3*3矩阵
val paramatrix1 = sc.parallelize(List(Vector(1, 1, 1), Vector(1, 2, 3),Vector(1, 3, 6), Vector(2, 1, 3), Vector(2, 2, 2), Vector(2, 3, 5), Vector(3, 1, 1), Vector(3, 2, 2), Vector(3, 3, 4)))//c(1,3,1,3,2,2,6,5,4)
val paramatrix2 =sc.parallelize(List(Vector(1, 1, 5), Vector(1, 2, 3),Vector(1, 3, 3), Vector(2, 1, 1), Vector(2, 2, 6), Vector(2, 3, 7), Vector(3, 1, 4), Vector(3, 2, 1), Vector(3, 3, 8)))//
结果为Array(((3.0,1.0),23.0), ((2.0,3.0),63.0), ((1.0,2.0),27.0), ((1.0,3.0),72.0), ((2.0,1.0),37.0), ((1.0,1.0),32.0), ((2.0,2.0),26.0), ((3.0,2.0),19.0), ((3.0,3.0),49.0)),正确。
瓶颈可能在cartesian处。以后有条件了,会把大规模集群的结果贴上来看看。