5/31 AprioriAll算法研究（2）

历经饱受折磨的一天，我总算是实现出来了这个算法。实话说看懂了之后实现起来困难不是特别大，但就是相当的繁琐。这个算法步骤太多，因此代码量也很多，好在寻找频繁项集的过程和寻找频繁序列的过程比较像，写起来稍稍有些宽慰。

另外，这里是用的我更熟悉的java写的（但是说起来一点也不面向对象了），而且也几乎写了逐行注释，最后加起来有六百行。。。

package aprioriAll;

import java.io.*;
import java.util.*;
import java.util.Map.Entry;

public class AprioriAll {

	public static void main(String[] args) {
		AprioriAllCalculation ap = new AprioriAllCalculation();

		ap.aprioriAllProcess();
	}
}

class AprioriAllCalculation

{
	/**
	 * 三维数组，代表一个序列数据库，维度是：事务，序列，事件桶（用户，周，访问列表）
	 */
	Vector>> data = null;
	
	/**
	 * 事件列表
	 */
	Vector itemList = null;
	
	/**
	 * 频繁n-序列集合	
	 */
	Vector> litemset = null;
	
	/**
	 * 序列到整数映射
	 */
	HashMap, Integer> litemMaps = null;
	/**
	 * 把事件转换为频繁项集后的客户信息序列
	 */
	Vector>>> transformedSequence = null;
	/**
	 * 转换后再映射到整数的客户信息序列
	 */
	Vector>> transformedMappedSequence = null;
	Vector> seqItemset = null;
	/**
	 * 频繁序列候选集
	 */
	Vector> seqCandidates = new Vector>();
	Vector mappedItemList = null;
	/**
	 * 记录每个客户所包含的1-频繁序列
	 */
	Vector> seqData = null;
	/**
	 * 最大频繁序列
	 */
	Vector> maximalLargeSequence = null;
	/**
	 * 结果集
	 */
	Vector>> resultSet = null;

	/**
	 * 当前频繁n-项集的候选项集集合
	 */
	Vector> candidates = new Vector>();
	
	String configFile = "src/aprioriAll/config.txt"; // 配置文件
	String transaFile = "src/aprioriAll/transa.txt"; // 数据文件
	String outputFile = "src/aprioriAll/aprioriAll-output.txt";// 输出文件
	int numItems; // n-计数用
	int numTransactions; // 事务数
	double minSupRatio; // 最小支持度
	double minSupNumber; // 最小支持频数
	String itemSep = " "; // 数据库中每行的分隔符

	public void aprioriAllProcess() {
		getConfig(); // 获取配置 用户个数和最小支持度

		// 排序阶段
		System.out.println("...Sort Phase....\n");
		SortPhase();
		System.out.println("Phase 1 is completed\n");
		System.out.println("data : " + data + "\n\n");
		// 频繁项集阶段
		System.out.println("...Litem Phase....\n");
		LitemPhase();
		System.out.println("Phase 2 is completed\n");
		System.out.println("litemset : " + litemset + "\n\n");
		// 把项映射成整数，方便计算
		MapCreation();
		//转换阶段
		System.out.println("...Transformation Phase....\n");
		TransformationPhase();
		System.out.println("Phase 3 is completed\n");
		System.out.println("mapped sequence : " + transformedMappedSequence + "\n\n");
		//序列阶段
		System.out.println("...Sequence Phase....\n");
		SequencePhase();
		System.out.println("Phase 4 is completed\n");
		System.out.println("Sequence Item Set : " + seqItemset + "\n\n");
		//最大化阶段
		System.out.println("...Maximal Phase....\n");
		MaximalPhase();
		System.out.println("Phase 5 is completed\n");

		System.out.println("Result is : \n" + resultSet);
	}

	/**
	 * 获取配置
	 * 包括事务（用户）个数和最小支持度
	 */
	private void getConfig() {
		FileWriter fw;
		BufferedWriter file_out;
		try {
			FileInputStream file_in = new FileInputStream(configFile);
			BufferedReader data_in = new BufferedReader(new InputStreamReader(file_in));

			// 事务（用户）数
			numTransactions = Integer.valueOf(data_in.readLine()).intValue();
			// 最小支持度（百分比）
			minSupRatio = (Double.valueOf(data_in.readLine()).doubleValue());

			// 输出到控制台
			System.out.print("\nInput configuration: " + numItems + " items, " + numTransactions + " transactions, ");
			System.out.println("minsup = " + minSupRatio + "%");
			System.out.println();
			minSupNumber = minSupRatio / 100 * numTransactions;

			// 创建输出文件
			fw = new FileWriter(outputFile);
			file_out = new BufferedWriter(fw);
			// 输出测试 事务数
			file_out.write(numTransactions + "\n");
			file_out.close();
		} catch (IOException e) {
			System.out.println(e);
		}
	}

	/**
	 * 排序阶段
	 * 读取数据库中的数据，生成一个以三维数组表示的数据集
	 */
	private void SortPhase() {

		data = new Vector>>();
		itemList = new Vector();
		FileInputStream file_in; // 文件输入流
		BufferedReader data_in; // 数据输入流
		StringTokenizer stFile;

		try {
			// 加载数据文件
			file_in = new FileInputStream(transaFile);
			data_in = new BufferedReader(new InputStreamReader(file_in));

			int i = 0;
			while (i < numTransactions) {
				// 获取序列
				Vector> sequence = new Vector>();
				while (true) {
					stFile = new StringTokenizer(data_in.readLine(), itemSep);
					if (stFile.countTokens() == 0) {
						break;
					} else {
						// 获取序列中的事件桶
						Vector basket = new Vector();
						while (stFile.hasMoreTokens()) {
							// 获取事件桶中的事件并添加
							String item = stFile.nextToken();
							basket.add(item);
							// 同时构建事件列表（1-项集）
							if (!itemList.contains(item)) {
								itemList.add(item);
							}
						}
						// 添加到序列
						sequence.add(basket);
					}
				}
				// 添加到事务集
				data.add(sequence);
				i++;
			}
		}

		catch (IOException e) {
			System.out.println(e);
		}

	}

	/**
	 * 频繁项集阶段
	 * 从1-项集开始，寻找符合最小支持度的候选项
	 * 自连接产生下一项集，寻找符合最小支持度的候选项
	 * 循环直到自连接不出来下一项集
	 * 这样生成出来了频繁1-序列
	 */
	private void LitemPhase() {

		int itemsetNumber = 0; // 当前是n-项集
		numItems = itemList.size();

		litemset = new Vector>();
		System.out.println("Apriori algorithm has started for litem phase...\n");

		// while not complete
		do {
			// 计数当前要检查n-项集
			itemsetNumber++;

			// 生成候选集
			generateCandidates(itemsetNumber);

			// 检查支持度
			calculateFrequentItemsets(itemsetNumber);
			// 频繁n-项集
			if (candidates.size() != 0) {
				System.out.println("Frequent " + itemsetNumber + "-itemsets");
				System.out.println(candidates);
			}
			//把频繁n-项集中的候选添加到频繁序列中
			litemset.addAll(candidates);
			// 如果频繁项集中小于等于1项，那就已经结束了
		} while (candidates.size() > 1);

	}

	/**
	 * 生成频繁1-序列和整数的映射
	 */
	private void MapCreation() {

		litemMaps = new HashMap, Integer>();
		for (int i = 1; i < litemset.size() + 1; i++) {
			litemMaps.put(litemset.get(i - 1), i);
		}

	}

	/**
	 * 转换阶段
	 * 每个事件被包含于该事件中所有频繁项集替换。
	 * 如果一个事件不包含任何频繁项集，则将其删除。
	 * 如果一个客户序列不包含任何频繁项集，则将该序列删除。
	 */
	private void TransformationPhase() {

		transformedMappedSequence = new Vector>>();
		transformedSequence = new Vector>>>();
		seqData = new Vector>();

		// 对每一个客户
		for (int i = 0; i < data.size(); i++) {
			int count = 0;
			transformedSequence.add(new Vector>>());
			transformedMappedSequence.add(new Vector>());
			seqData.add(new Vector());
			// 对每一个序列
			for (int j = 0; j < data.get(i).size(); j++) {
				transformedSequence.get(i).add(new Vector>());
				transformedMappedSequence.get(i).add(new Vector());
				// 检查频繁1-序列中的每个序列
				for (int k = 0; k < litemset.size(); k++) {
					// 如果这个客户的这个序列的事件集中包含这个频繁序列
					if (data.get(i).get(j).containsAll(litemset.get(k))) {
						// 把这个频繁序列记录到这个客户的这个事件集中（j-count是因为有需要删除的事件集）
						transformedSequence.get(i).get(j - count).add(litemset.get(k));
						// 映射成整数的那个也加上
						transformedMappedSequence.get(i).get(j - count).add(litemMaps.get(litemset.get(k)));
						seqData.get(i).add(litemMaps.get(litemset.get(k)));
					}
				}
				// 如果检查完频繁序列集 发现这个客户的这个事件集里没有频繁序列
				if (transformedSequence.get(i).get(j - count).isEmpty()) {
					// 那么删除这个事件集
					transformedSequence.get(i).remove(j - count);
					transformedMappedSequence.get(i).remove(j - count);
					// 计数
					count++;
				}
			}
		}
	}

	/**
	 * 产生频繁序列阶段
	 * 利用转换后的序列数据库寻找频繁序列
	 */
	public void SequencePhase() {

		// 记录现在是n-序列
		int itemsetNumber = 0;

		seqItemset = new Vector>();

		System.out.println("Apriori algorithm has started for Sequence Phase\n");

		do {
			itemsetNumber++;
			// 生成候选集
			generateSeqCandidates(itemsetNumber);
			// 检查支持度
			calculateSeqFrequentItemsets(itemsetNumber);
			if (seqCandidates.size() != 0) {
				System.out.println("Frequent " + itemsetNumber + "-itemsets");
				System.out.println(seqCandidates);
			}
			// 在频繁序列集中添加频繁序列候选集
			seqItemset.addAll(seqCandidates);
			// 和检查频繁项集类似 直到频繁候选集中小于等于一个，就代表结束了
		} while (seqCandidates.size() > 1);

	}

	/**
	 * 生成n项集的候选集
	 * @param n 从n-项集开始生成
	 */
	private void generateCandidates(int n) {

		Vector> tempCandidates = new Vector>(); // 临时候选集
		Vector tempElementVec;
		Vector tempElementVec2;
		// 如果是1-项集，那就是所有的事件
		if (n == 1) {
			for (int i = 0; i < numItems; i++) {
				tempElementVec = new Vector();
				tempElementVec.add(itemList.elementAt(i));
				tempCandidates.add(tempElementVec);
			}
		} else if (n == 2) // 如果是2项集，那就是1项集两两组合
		{
			

			for (int i = 0; i < candidates.size(); i++)
				for (int j = i + 1; j < candidates.size(); j++) {
					tempElementVec = new Vector();
					tempElementVec.add(candidates.get(i).get(0));
					tempElementVec.add(candidates.get(j).get(0));
					tempCandidates.add(tempElementVec);

				}

		} else { 	
			// 对于其他项集，需要做自连接，即检查每一(n-1)-项和之后的另一(n-1)-项，如果这两个的前n-2项都一样，就可以做连接
			// 例如生成3-项集，已有2-项集是[[40,70],[40,80]],检查他们俩的前1项，一样，就把两个的最后一项也合起来得到[40,70,80]

			for (int i = 0; i < candidates.size(); i++) {

				for (int j = i + 1; j < candidates.size(); j++) {
					tempElementVec = new Vector();
					tempElementVec2 = new Vector();

					for (int s = 0; s < n - 2; s++) {
						tempElementVec.add(candidates.get(i).get(s));
						tempElementVec2.add(candidates.get(j).get(s));
					}

					if (tempElementVec.equals(tempElementVec2)) {
						tempElementVec.add(candidates.get(i).get(n - 2));
						tempElementVec.add(candidates.get(j).get(n - 2));
						tempCandidates.add(tempElementVec);
					}
				}
			}
		}

		candidates.clear();

		candidates = new Vector>(tempCandidates);
		tempCandidates.clear();
	}

	/**
	 * 计算候选集中各个候选项集是否符合最小支持度
	 * @param n n-项集
	 */
	private void calculateFrequentItemsets(int n) {

		Vector> TempCandidates = new Vector>();
		Boolean[] flags;
		int count;
		// 对每一候选项集
		for (Vector cand : candidates) {

			flags = new Boolean[data.size()];
			// 对数据集中每一顾客
			for (Vector> customer : data) {

				int a = data.indexOf(customer);
				// 对每一事务的每一事件桶
				for (Vector basket : customer) {
					// 如果包含候选集
					if (basket.containsAll(cand)) {
						// 标记包含
						flags[a] = true;
						break;

					}

				}
				if (flags[a] == null)
					flags[a] = false;

			}
			// 统计
			count = 0;
			for (Boolean flag : flags)
				if (flag)
					count++;
			// 如果大于最小支持度则留下
			if (count >= minSupNumber)
				TempCandidates.add(cand);

		}


		candidates.clear();

		candidates = new Vector>(TempCandidates);
		TempCandidates.clear();

	}

	/**
	 * 由n-1序列生成n序列
	 * @param n
	 */
	private void generateSeqCandidates(int n) {

		// 储存当前候选序列
		Vector> tempCandidates = new Vector>(); 
		Vector tempElementVec;
		Vector tempElementVec2;
		// 如果是1-序列，那么里面就是所有的代表频繁序列的整数（类似找频繁项集）
		if (n == 1) {
			for (int i = 1; i <= litemMaps.size(); i++) {
				tempElementVec = new Vector();
				tempElementVec.add(i);
				tempCandidates.add(tempElementVec);
			}
		}

		else if (n == 2) // 2-序列就是1-序列两两组合
		{


			for (int i = 0; i < seqCandidates.size(); i++)
				for (int j = i + 1; j < seqCandidates.size(); j++) {
					tempElementVec = new Vector();
					tempElementVec.add(seqCandidates.get(i).get(0));
					tempElementVec.add(seqCandidates.get(j).get(0));
					tempCandidates.add(tempElementVec);

				}

		} else {
			// 其他n-序列
			for (int i = 0; i < seqCandidates.size(); i++) {
				// 每一个和后面的比较 类似于n-项集
				for (int j = i + 1; j < seqCandidates.size(); j++) {
					tempElementVec = new Vector();
					tempElementVec2 = new Vector();

					for (int s = 0; s < n - 2; s++) {
						tempElementVec.add(seqCandidates.get(i).get(s));
						tempElementVec2.add(seqCandidates.get(j).get(s));
					}

					if (tempElementVec.equals(tempElementVec2)) {
						tempElementVec.add(seqCandidates.get(i).get(n - 2));
						tempElementVec.add(seqCandidates.get(j).get(n - 2));
						tempCandidates.add(tempElementVec);
					}
				}
			}
		}
		// 清空
		seqCandidates.clear();
		// 刷新
		seqCandidates = new Vector>(tempCandidates);
		tempCandidates.clear();
	}
	/**
	 * 计算频繁序列 是否符合支持度
	 * @param n
	 */
	private void calculateSeqFrequentItemsets(int n) {

		Vector> TempCandidates = new Vector>();
		Boolean[] flags;
		int count;
		// 对每一个候选序列
		for (Vector can : seqCandidates) {

			flags = new Boolean[seqData.size()];
			// 对每一个序列数据集中的用户包含的序列
			for (int i = 0; i < seqData.size(); i++) {
				Vector cand = new Vector(can);
				Vector customer = new Vector(seqData.get(i));
				while (cand.size() > 0 && customer.size() > 0) {
					// 检查是否可以匹配到这个序列（用了一种“跳过不匹配”的巧妙方式）
					if (cand.get(0).equals(customer.get(0))) {
						cand.remove(0);
					} else {
						customer.remove(0);
					}
				}
				// 如果频繁序列每一个都匹配到了那么标志为有
				if (cand.size() == 0)
					flags[i] = true;
				else
					flags[i] = false;

			}
			// 计数
			count = 0;
			for (Boolean flag : flags)
				if (flag)
					count++;

			if (count >= minSupNumber)
				TempCandidates.add(can);
		}

		// 清空
		seqCandidates.clear();
		// 把临时的候选序列赋值过来
		seqCandidates = new Vector>(TempCandidates);
		TempCandidates.clear();

	}

	/**
	 * 最大化阶段
	 * 目的是把频繁序列集中的 可以认为是其他频繁序列集的子序列集 的序列集 删去
	 */
	private void MaximalPhase() {
		// 找最长序列
		maximalLargeSequence = new Vector>();
		Vector> tempSequenceSet = new Vector>(seqItemset);

		// 对频繁序列集中的每个频繁序列
		for (Vector seqs : seqItemset) {
			int check = 0;
			// 拿出来一个
			tempSequenceSet.remove(seqs);

			// 对剩下的每一个
			for (Vector checkSeq : tempSequenceSet) {
				// 检查是否包含拿出来那个
				if (checkSeq.containsAll(seqs)) {
					check = 1;
				}
			}
			// 都不包含就放到最大序列里
			if (check == 0) {
				maximalLargeSequence.add(seqs);
			}
		}
		// 按最大序列的整数在map里查找出来原来的值
		resultSet = new Vector>>();
		// 对最大序列中的每一个序列
		for (Vector seq : maximalLargeSequence) {
			resultSet.add(new Vector>());
			for (int i = 0; i < seq.size(); i++) {
				for (Entry, Integer> ent : litemMaps.entrySet()) {
					if (ent.getValue() == seq.get(i)) {
						resultSet.get(maximalLargeSequence.indexOf(seq)).add(ent.getKey());
					}
				}
			}
		}

	}

	/**
	 * 输入方法
	 * @return 文本文档中的一行
	 */
	public static String getInput() {
		String input = "";
		
		BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

		
		try {
			input = reader.readLine();
		} catch (Exception e) {
			System.out.println(e);
		}
		return input;
	}

}

跑个测试样例看看：

30 
90 

10 20 
30 
40 60 70

30 50 70

30
40 70
90

90

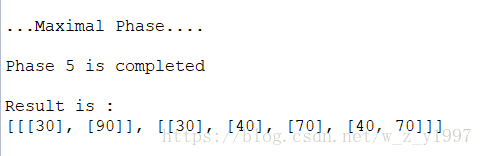
OK，成功找到最大频繁序列。下一步的工作就是基于频繁序列的推荐了，目前有两个思路，一个是检查一个用户的近期事务（例如本周，或者最近两周），是否是某一个最大频繁序列的子序列，如果是，推荐该最大频繁序列中，用户出现过序列之后的事件；另一个是检索用户历史事务中的每一个事件集，对于每一个事件集所在的最大频繁序列之后的事件集都计数一遍，按从多到少排序来推荐。这两个粗略一想，前一个是推荐序列，更符合最初知识图谱、学习路径的思路，后一个有种多个路径交叉点的感觉，可能推荐出来是比较重要的节点。明后两天实现出来看看效果吧。