【贪心】B036_LC_最多可以参加的会议数目（排序 / pq）

一、Problem

Given an array of events where events[i] = [startDayi, endDayi]. Every event i starts at startDayi and ends at endDayi.

You can attend an event i at any day d where startTimei <= d <= endTimei. Notice that you can only attend one event at any time d.

Return the maximum number of events you can attend.

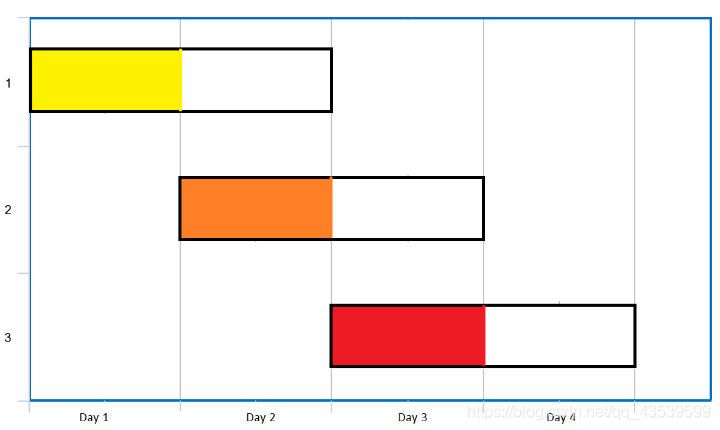
Input: events = [[1,2],[2,3],[3,4]]
Output: 3
Explanation: You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.

二、Solution

方法一：排序（超时）

思路

• 会议时间参差不齐，我们更希望看到是整齐的，那我们有两种选择：
  • 按照开始时间 s 升序排列
  • 按照结束时间 e 升序排列
  • 按照会议持续时间 e-s 升序排列
• 这两点我不清楚，但是我很明确参加结束时间越早的会议，我有更多的选择取参加其他会议，基于这点，我选择按第二点排序。

算法

• 排序…
• 如果参加了某一个正在进行会议，那么我们是无法在此期间参加其他会议的。
• 所以我们需要记录某一个会议的持续时间状态。
• 选择参加一个会议后，就立马枚举下一个会议了。

总之一句话：在所有时间里面找空隙，但很不幸超时了，对于 $[[1,1],[1,2],[1,3],[1,4],[1,n]]$ 这种事要遍历 $n^2$ 次。

class Solution {
    public int maxEvents(int[][] es) {
        Arrays.sort(es, (e1, e2) -> e1[1] - e2[1]);
        Set<Integer> now = new HashSet<>();
        for (int[] e : es)
        for (int i = e[0]; i <= e[1]; i++) {
            if (!now.contains(i)) {
                now.add(i);
                break;
            }
        } 
        return now.size();
    }
}

复杂度分析

• 时间复杂度：$O(n^2)$，
• 空间复杂度：$O(n)$，

---

方法二：pq

思想大题相同，用一个自变量 day 来记录天数，符合天数会议将结束时间的入队，过期的会议出队。

class Solution {
    public int maxEvents(int[][] es) {
        Arrays.sort(es, (e1, e2) -> e1[0] - e2[0]);
        Queue<Integer> q = new PriorityQueue<>();
        int i = 0, day = 1, n = es.length, cnt = 0;
        while (i < n || !q.isEmpty()) {
            while (i < n && es[i][0] == day)
                q.add(es[i++][1]);
            while (!q.isEmpty() && q.peek() < day)
                q.poll();
            if (!q.isEmpty()) {
                q.poll();
                cnt++;
            }
            day++;
        }
        return cnt;
    }
}

复杂度分析

• 时间复杂度：$O(nlogn)$，
• 空间复杂度：$O(n)$，