暑假集训考试R2 konomi 慕

题目描述

低気圧はこぶ頭痛だって　忘れる、キミに会えば

Hitomi 在数轴上放置了 nnn 种颜色的 2n2n2n 个棋子，每种颜色的棋子恰有两个。

Hitomi 希望在某个任选的点将数轴「对折」，使得所有 nnn 个同色棋子对之间的距离之和最小。当然啦，假设对折过程中棋子始终固定在数轴上。

Hitomi 需要计算这个最小值。

将数轴在 x=x0x = x_0x=x​0​​ 处「对折」可以视作对于每个坐标小于 x0x_0x​0​​ 的棋子，若其坐标为 x1x_1x​1​​，则将该棋子移至 x=2x0−x1x = 2x_0 - x_1x=2x​0​​−x​1​​ 处。

输入格式

从文件 konomi.in 读入数据。

输入的第一行包含一个整数 nnn。

接下来 nnn 行中的第 iii 行包含两个空格分隔的整数 pi,qip_i, q_ip​i​​,q​i​​，表示一对同色棋子的坐标。

棋子的坐标可能重复。

输出格式

输出到文件 konomi.out 中。

输出一个整数，表示合适地选取折叠点后，同色棋子对距离之和的最小值。可以证明这个值一定是个整数。

样例

样例输入 1

3
-3 4
0 5
1 6

样例输出 1

6

样例解释 1

将数轴在 x=2.5x = 2.5x=2.5 处对折，同色点对距离之和为 ∣8−4∣+∣5−5∣+∣4−6∣=6|8 - 4| + |5 - 5| + |4 - 6| = 6∣8−4∣+∣5−5∣+∣4−6∣=6。

样例输入 2

4
-5 0
-1 0
0 1
0 5

样例输出 2

7

样例解释 2

将数轴在 x=±2.5x = \pm 2.5x=±2.5 处对折，同色点对距离之和均为 777。

样例输入/输出 3

见「附加文件」中的 konomi3.in 与 konomi3.out。

分析

题目的名字听诡异的，就当是一种风格吧哈哈哈。

这道题没有AC吃亏就吃亏在我没有老老实实动笔写写画画，要吸取教训，以后做什么题目都要动笔写写画画，这样有时候就找到了突破口。我个人成功的案例就是去年NOIP D1T1，这个足够有说服力了吧。

说说这道题怎么想。首先我们要观察，会发现这个答案总是跟两点之间的中点有关。（枚举0.5的倍数也有16%，然而并不知道为什么没有拿分）

写写看公式。我们令f(x)是在横坐标为x处对折后得到的结果，应该有这样的形式：f(x) = Sum_{i = 1...n} g_i(x)

对于这个：g_i(x) =

q_i-p_i (xi || x>q_i)

2|x-(p_i+q_i)/2| (p_i≤x≤q_i)

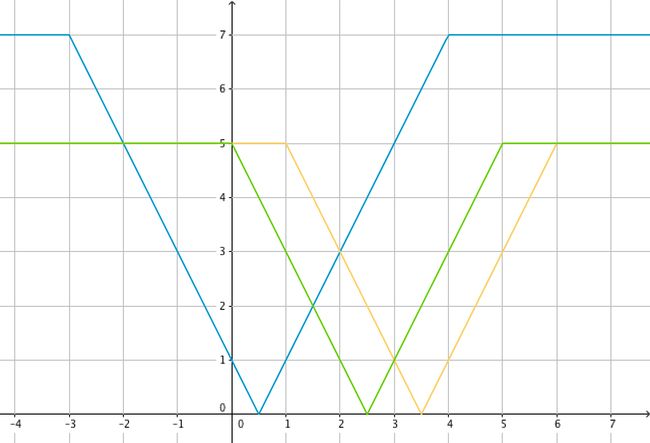
对于样例我们画一张图：

很形象地表现了g()的样子吧（偷了吕时清的图）

这样回到我们之前说的答案似乎总是和两个点或它们的中点有关，那么枚举每组这三个点。O(n²)也能拿到48%。

另外如果脑子清楚的，可以推出最优的对折位置是所有中点的中位数。当然也可以二分。（二分我想到了，但没敢画画图模拟一下f(i)的样子，最后不知道它是单峰函数就没敢写/倒）这样又可以骗到8%。（骗分出奇迹啊！）

最后讲讲这个100%算法。其实也是基于数学的想法的，我说可能说不太清，就直接贴吕时清老师怎么讲的。

• 考察f(x)的拐点，即所有g_i(x)拐点的并集

• 拐点之间f(x)的图像是⼀条直线段

• 在每个拐点，直线段的斜率增加或减少⼀定数值

• 各个g_i(x)的贡献独⽴

• 对于每个棋⼦对，创建三个拐点

• (p_i, -2)

• ((p_i+q_i)/2, +4)

• (q_i, -2)

• 排序后可以从左⾄右计算f(x)在所有拐点的值

大概能看懂吧？我觉得这段东西当中最重要的一句就是加粗划出的第三句话，在每个拐点，直线段的斜率都会改变。说白了这就是一个会在每个拐点上改变方向的折线，对吧？

程序

 1 #include 
 2 using namespace std;
 3 static const int MAXN = 1e5 + 4;
 4 int n;
 5 pair<int, int> ev[MAXN * 3];
 6 int main()
 7 {
 8     freopen("konomi.in", "r", stdin);
 9     freopen("konomi.out", "w", stdout);
10     scanf("%d", &n);
11     long long cur = 0;
12     for (int i = 0, p, q; i < n; ++i)
13     {
14         scanf("%d%d", &p, &q);
15         cur += q - p;
16         ev[i * 3 + 0] = make_pair(p + p, -1);
17         ev[i * 3 + 1] = make_pair(p + q, +2);
18         ev[i * 3 + 2] = make_pair(q + q, -1);
19     }
20     sort(ev, ev + n * 3);
21     long long ans = cur;
22     int slope = ev[0].second;
23     for (int i = 1; i < n * 3; ++i)
24     {
25         cur += (long long)slope * (ev[i].first - ev[i - 1].first);
26         ans = std::min(ans, cur);
27         slope += ev[i].second;
28     }
29     printf("%lld\n", ans);
30     return 0;
31 }

 

转载于:https://www.cnblogs.com/OIerPrime/p/9383918.html