KMP方法
str1 中是否有一个字符串(连续)或者子序列(可以不连续),等于
str2.字串(连续)和子数组(连续)。
把str1='abdsc', str2='bd'。
最长前缀和最长后缀:不包含0和-1.
在str1中,在在字符串中某一个字符的从1开始的k字符为前缀,s的2阶前缀为ab,后缀为ds。
mancher算法
从一个文件中找到最大回文字符串。
1211 加入特殊字符串,#1#2#1#1#按字符位置进行遍历,进行查看是否有最大回文。
回文半径:回文的最大边界
回文中心:回文的中心
BFPRT算法
数组的中位数,
- 数组分组,每个组由5个数
- 每个组内进行排序
- 每个组中位数拿出来进行组合新的数组,下中文数
- 递归调用bfprt算法
- 最大值减去最小值小于或等于num的子数组数量
给定数据arr和整数num,共返回有多少个子数组满足如下情况:
max(arr[i..j]) - min(arr[i..j]) <= num
max(arr[i..j])表示子数组max(arr[i..j])中的最大值,min(arr[i..j])表示子数组arr[i..j]中的最小值。
如果数组的长度为N,请实现解法
单调栈
所有树结构中,某一个数值k,n=左边>k,m=右边>k。一个栈中,栈底是大值,栈顶是小值。[5,4,3,6],把数组放入栈中,得到[5,4,3]当需要把6放入栈时,发现6>3,所以需要把[5,4,3]弹出,建立信息表,把6压栈。
1
通过单调栈构建大根堆,通过基本流程构建大根堆,就可以得到每个数据中的头部为最大值。
求最大子矩阵的大小
给定一个整形矩阵map,其中的值只有0和1两种,求其全时1的所有矩阵区域中,最大的矩阵区域为1的数量。从一个环形数组中找到可见山峰
- 0对
- 2对
- (2 x n)-3 对
通过单调栈,把大值放到底下,小值放在上面,如果遇到比小值大的值就开始弹出小值,对小值进行结算。
搜索二叉树
从头结点看,左节点 < 头部,右节点>头部,相等的节点压在一起。
设计一个getMin的栈
class MyStack2:
def __init__(self,):
self.stackData = [];
self.stackMin = [];
def push(self, newNum):
if (len(self.stackMin)==0):
self.stackMin.append(newNum)
elif (newNum < self.getMin()):
self.stackMin.append(newNum)
else:
self.stackMin.append(self.stackMin[-1])
self.stackData.append(newNum)
def pop(self):
if (len(self.stackData) == 0):
return None
self.stackMin.pop()
return self.stackData.pop()
def getMin(self):
if (len(self.stackMin)==0):
return None
return self.stackMin[-1]
stack = [1,2,3,3,5]
stack1 = MyStack2()
for i in stack:
stack1.push(i)
stack1.getMin()
print(stack1.getMin())
两个栈组成的队列
class TwoStackQueue:
def __init__(self):
self.stackPush = []
self.stackPop = []
def add(self, pushInt):
self.stackPush.append(pushInt)
def poll(self):
if len(self.stackPop) == 0 and len(self.stackPush) == 0:
return None
elif len(self.stackPop) == 0:
while self.stackPush:
self.stackPop.append(self.stackPush.pop())
return self.stackPop.pop()
def peek(self):
if len(self.stackPop) == 0 and len(self.stackPush) == 0:
return None
elif len(self.stackPop) == 0:
while self.stackPush:
self.stackPop.append(self.stackPush.pop())
return self.stackPop[len(self.stackPop)-1]
queue = [1,2,3,3]
queue1 = TwoStackQueue()
for i in queue:
queue1.add(i)
print(queue1.peek())
print(queue1.poll())
print(queue1.peek())
使用递归函数实现栈的逆序
def getAndRemoveLastElement(stack):
result = stack.pop()
if len(stack) == 0:
return result
else:
last = getAndRemoveLastElement(stack)
stack.append(result)
return last
def reverse(stack):
if len(stack) == 0:
return None
last = getAndRemoveLastElement(stack)
reverse(stack)
stack.append(last)
stack = [1,2,3,4]
#print(getAndRemoveLastElement(stack))
print(reverse(stack))
print(stack)
猫狗队列
class Pet:
def __init__(self,type):
self.type = type
def getPettype(self):
return self.type
class Dog(Pet):
def __init__(self,):
#Pet.__init__(self,'dog')
super(Dog,self).__init__('dog')
class Cat(Pet):
def __init__(self,):
#Pet.__init__(self,'cat')
super(Cat,self).__init__('cat')
class PetEnterQueue:
def __init__(self, pet, count):
self.pet = pet
self.count = count
def getPet(self):
return self.pet
def getCount(self):
return self.count
def getEnterPetType(self):
return self.pet.getPettype()
class DogCatQueue:
def __init__(self,):
self.dogQ = []
self.catQ = []
self.count = 0
def add(self, pet):
if pet.getPettype() == 'dog':
self.dogQ.append(PetEnterQueue(pet, self.count))
self.count += 1
elif pet.getPettype() == 'cat':
self.catQ.append(PetEnterQueue(pet, self.count))
self.count += 1
else:
return None
def pollAll(self):
if (not (len(self.dogQ) ==0)) and (not (len(self.catQ) == 0)):
if (self.dogQ[len(self.dogQ)-1].getCount() < self.catQ[len(self.catQ)-1].getCount()):
return self.dogQ.pop().getPet()
else:
return self.catQ.pop().getPet()
def pollDog(self):
if not(len(self.dogQ) == 0):
return self.dogQ.pop().getPet()
return None
def pollCat(self):
if not(len(self.catQ) == 0):
return self.catQ.pop().getPet()
return None
def isEmpty(self):
return (len(self.dogQ) ==0) and (len(self.catQ) == 0)
def isDogQueueEmpty(self):
return (len(self.dogQ) ==0)
def isCatQueueEmpty(self):
return (len(self.catQ) ==0)
queue = [Dog(),Dog(), Cat(), Dog(), Cat()]
queue1 = DogCatQueue()
for i in queue:
queue1.add(i)
print(queue1.isDogQueueEmpty())
用一个栈实现另一个栈的排序
def sortStackByStack(stack):
help = []
while not(len(stack) ==0):
cur = stack.pop()
while not (len(help) ==0) and (help[len(help) - 1] > cur):
stack.append(help.pop())
help.append(cur)
while not(len(help)==0):
stack.append(help.pop())
stack = [1,3,2,4,2]
sortStackByStack(stack)
print(stack)
生成窗口最大值数组
有一个整数数组arr和一个大小为w的窗口从数组的最左边滑到最右边,窗口每次由滑一个位置。
使用res收集最大值。
import collections
def getMaxWindow(arr, w):
if (not arr ) or (w < 1) or (len(arr) < w):
return None
qmax = collections.deque()
res = [0] * (len(arr) - w + 1)
index = 0
for i in range(len(arr)):
while (not (len(qmax) == 0)) and (arr[qmax[len(qmax) - 1]] <= arr[i]):
qmax.pop()
qmax.append(i)
if qmax[0] == (i-w):
qmax.popleft()
if (i >= (w-1)):
res[index] = arr[qmax[0]]
index += 1
return res
arr = [3,5,1,2,2,7,3,9]
print(getMaxWindow(arr, 3))
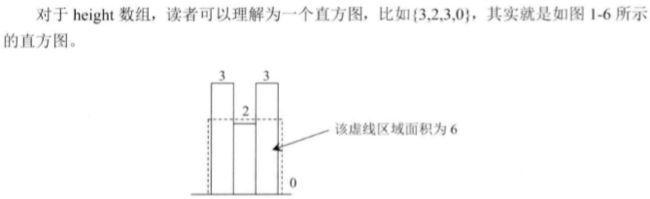
求最大子矩阵的大小
依次以每一层进行分割,进行每一层的数字叠加,每分割一次就进行一次计算。
def maxRecSize(map):
if not (map) :
return 0
maxArea = 0
height = [0] * len(map[0])
for i in range(len(map)):
for j in range(len(map[0])):
height[j] = height[j] + 1
if map[i][j] == 0:
height[j] = 0
maxArea = max(maxRecFromBottom(height), maxArea)
return maxArea
def maxRecFromBottom(height):
if not height:
return 0
stack = []
maxArea = 0
for i in range(len(height)):
while stack and height[i] <= height[stack[len(stack) - 1]]:
j = stack.pop()
k = -1
if stack:
k = stack[len(stack)-1]
curArea = (i - k -1) * height[j]
maxArea = max(maxArea,curArea)
stack.append(i)
while stack:
j = stack.pop()
k = -1
if stack:
k = stack[len(stack)-1]
curArea = (len(height) - k -1) * height[j]
maxArea = max(maxArea,curArea)
return maxArea
map = [[1,0,1,1],
[1,1,1,1],
[1,1,1,0]]
print(maxRecSize(map))