DP动态规划
https://www.cnblogs.com/wuyuegb2312/p/3281264.html#q3a1
硬币找零
假设有几种硬币,如1、3、5,并且数量无限。请找出能够组成某个数目的找零所使用最少的硬币数
动态规划的基本思想是将待求解问题分解成若干个子问题,先求解子问题,并将这些子问题的解保存起来,如果以后在求解较大子问题的时候需要用到这些子问题的解,就可以直接取出这些已经计算过的解而免去重复运算。保存子问题的解可以使用填表方式,例如保存在数组中。
用一个实际例子来体现动态规划的算法思想——硬币找零问题。
硬币找零问题描述:现存在一堆面值为 V1、V2、V3 … 个单位的硬币,问最少需要多少个硬币才能找出总值为 T 个单位的零钱?假设这一堆面值分别为 1、2、5、21、25 元,需要找出总值 T 为 63 元的零钱。
很明显,只要拿出 3 个 21 元的硬币就凑够了 63 元了。
基于上述动态规划的思想,我们可以从 1 元开始计算出最少需要几个硬币,然后再求 2 元、3元…每一次求得的结果都保存在一个数组中,以后需要用到时则直接取出即可。那么我们什么时候需要这些子问题的解呢?如何体现出由子问题的解得到较大问题的解呢?
其实,在我们从 1 元开始依次找零时,可以尝试一下当前要找零的面值(这里指 1 元)是否能够被分解成另一个已求解的面值的找零需要的硬币个数再加上这一堆硬币中的某个面值之和,如果这样分解之后最终的硬币数是最少的,那么问题就得到答案了。
单是上面的文字描述太抽象,先假定以下变量:
values[] : 保存每一种硬币的币值的数组
valueKinds :币值不同的硬币种类数量,即values[]数组的大小
money : 需要找零的面值
coinsUsed[] : 保存面值为 i 的纸币找零所需的最小硬币数
算法描述:
当求解总面值为 i 的找零最少硬币数 coinsUsed[ i ] 时,将其分解成求解 coinsUsed[ i – cents]和一个面值为 cents 元的硬币,由于 i – cents < i , 其解 coinsUsed[ i – cents] 已经存在,如果面值为 cents 的硬币满足题意,那么最终解 coinsUsed[ i ] 则等于 coinsUsed[ i – cents] 再加上 1(即面值为 cents)的这一个硬币。
package DP;
public class 最小硬币数 {
public static void makeChange(int[] values, int valueKinds, int money, int[] coinsUsed){
coinsUsed[0] = 0;
for (int i = 1; i < money; i++) {
int min = i;
for (int j = 0; j < valueKinds; j++) {
if(values[j] <= i){
int temp = coinsUsed[i - values[j]] + 1;
if(temp < min){
min = temp;
}
}
}
coinsUsed[i] = min;
System.out.println("面值为" + i + "的最小硬币数为:" + coinsUsed[i]);
}
}
public static void main(String[] args) {
// 硬币面值预先已经按降序排列
int[] coinValue = new int[] {25, 21, 10, 5, 1};
// 需要找零的面值
int money = 63;
// 保存每一个面值找零所需的最小硬币数,0号单元舍弃不用,所以要多加1
int[] coinsUsed = new int[money + 1];
makeChange(coinValue, coinValue.length, money, coinsUsed);
}
}
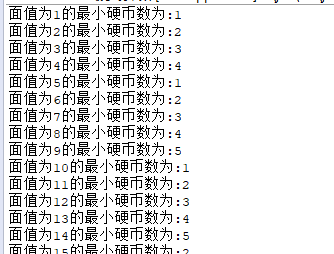
结果:
分析:
总结:
Java 比较两个字符串的相似度算法(Levenshtein Distance)
- 将问题拆分,拆成一个个子问题
- 维护一个数组,用于记录从1到63的最少硬币数量
- 每次比较最小的一定要和coinsUsed[i - values[j]] + 1比较
package DP;
public class 两个字符串相似度算法 {
private static int compare(String str, String target){
int[][] d;
int n = str.length();
int m = target.length();
d = new int[n + 1][m + 1];
char ch1;
char ch2;
int temp;
for (int i = 0; i <= n; i++) {
d[i][0] = i;
}
for (int i = 0; i <= m; i++) {
d[0][i] = i;
}
for (int i = 1; i <= n; i++) {
ch1= str.charAt(i-1);
for (int j = 1; j <= m; j++) {
ch2 = target.charAt(j-1);
if(ch1==ch2 || ch1==ch2+32 || ch2==ch1+32){
temp = 0;
}else{
temp = 1;
}
d[i][j] = min(d[i-1][j] + 1, d[i][j-1] + 1, d[i-1][j-1] + temp);
}
}
return d[n][m];
}
private static int min(int one, int two, int three){
return (one = one < two ? one: two) < three ? one : three;
}
public static float getSimilarityRatio(String str, String target) {
int max = Math.max(str.length(), target.length());
return 1 - (float) compare(str, target) / max;
}
public static void main(String[] args) {
String a= "Steel";
String b = "Steel Pipe";
System.out.println("相似度:"+getSimilarityRatio(a,b));
}
//这个是从网上直接下载的
private static int compare1(String str, String target) {
int d[][];
// 矩阵
int n = str.length();
int m = target.length();
int i;
// 遍历str的
int j;
// 遍历target的
char ch1;
// str的
char ch2;
// target的
int temp;
// 记录相同字符,在某个矩阵位置值的增量,不是0就是1
if (n == 0) {
return m;
}
if (m == 0) {
return n;
}
d = new int[n + 1][m + 1];
// 初始化第一列
for (i = 0; i <= n; i++) {
d[i][0] = i;
}
// 初始化第一行
for (j = 0; j <= m; j++) {
d[0][j] = j;
}
for (i = 1; i <= n; i++) {
// 遍历str
ch1 = str.charAt(i - 1);
// 去匹配target
for (j = 1; j <= m; j++) {
ch2 = target.charAt(j - 1);
if (ch1 == ch2 || ch1 == ch2 + 32 || ch1 + 32 == ch2) {
temp = 0;
} else {
temp = 1;
}
// 左边+1,上边+1, 左上角+temp取最小
d[i][j] = min(d[i - 1][j] + 1, d[i][j - 1] + 1, d[i - 1][j - 1] + temp);
}
}
return d[n][m];
}
}
输出结果:
根据程序算出来的结果是5,而我自己手推算出来的是4,不过没关系了,大体意思明白就可了,下面附上手推的结果,作为一个借鉴吧,肯定在某一处存在问题,但是不想找了
算法简介:
Levenshtein Distance,又称编辑距离,指的是两个字符串之间,由一个转换成另一个所需的最少编辑操作次数。
许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
编辑距离的算法是首先由俄国科学家Levenshtein提出的,故又叫Levenshtein Distance。
算法原理:
该算法的解决是基于动态规划的思想,具体如下:
设 s 的长度为 n,t 的长度为 m。如果 n = 0,则返回 m 并退出;如果 m=0,则返回 n 并退出。否则构建一个数组 d[0..m, 0..n]。
将第0行初始化为 0..n,第0列初始化为0..m。
依次检查 s 的每个字母(i=1..n)。
依次检查 t 的每个字母(j=1..m)。
如果 s[i]=t[j],则 cost=0;如果 s[i]!=t[j],则 cost=1。将 d[i,j] 设置为以下三个值中的最小值:
紧邻当前格上方的格的值加一,即 d[i-1,j]+1
紧邻当前格左方的格的值加一,即 d[i,j-1]+1
当前格左上方的格的值加cost,即 d[i-1,j-1]+cost
重复3-6步直到循环结束。d[n,m]即为莱茵斯坦距离。
最长公共子序列
一个序列S任意删除若干个字符得到新序列T,则T称为S的子序列。若两个序列X和Y的公共子序列中,长度最长的那个字序列称为X和Y的最长公共子序列(LCS)。
Xi表示字符串的前i个字符,Yj表示字符串的前j个字符,它们的公共子序列记为:LCS(X,Y),即Z=
1)Xm == Yn(最后一个字符相同),则Xm与Yn的最长公共子序列Zk的最后一个字符必定相同,即:Xm == Yn == Zk。此时的表达式为:
LCS(Xm, Yn) = LCS(Xm-1, Yn-1) +Xm (**公式一**)
2)Xm != Yn(最后一个字符不相同),则Xm与Yn的最长公共子序列Zk的最后一个字符就存在两种肯能,即:Xm == Zk 或者 Yn == Zk。此时的表达式存在两种情况,如下:
LCS(Xm, Yn) = LCS(Xm-1, Yn) 或者 LCS(Xm, Yn) = LCS(Xm, Yn-1)。则最终的表达式为:
LCS(Xm, Yn) = MAX{LCS(Xm-1, Yn), LCS(Xm, Yn-1)} (**公式二**)
在寻找最长公共子序列的过程中利用数组Array来记录Xi和Yj的最长公共子序列的长度。当i=0或j=0时,Array数组记录为0。当i>0,j>0并且Xi==Yj时,利用公式一,当i>0,j>0,并且Xi!= Yj时,利用公式二。得到如下公式:
Array(i,j) = 0; 当i=0或者j=0;
Array(i,j) = Array(i-1,j-1); 当i>0,j>0&&Xi==Yj;
Array(i,j) = max{Array(i-1,j),Array(I,j-1)} 当i>0,j>0&&Xi!=Yj
package DP;
import java.util.Stack;
public class 最长公共子序列 {
public static void getLCS(String x, String y){
char[] s1 = x.toCharArray();
char[] s2 = y.toCharArray();
int[][] array = new int[x.length() + 1][y.length() + 1];
int i;
int j;
for (i = 0; i < array.length; i++) {
array[i][0] = 0;
}
for (j = 0; j < array[0].length; j++) {
array[0][j] = 0;
}
for (int m = 1; m < array.length; m++) {
for (int k = 1; k < array[0].length; k++) {
if(s1[m-1] == s2[k-1]){
array[m][k] = array[m-1][k-1] + 1;
}else{
array[m][k] = max(array[m-1][k], array[m][k-1]);
}
}
}
System.out.println(array[x.length()][y.length()]);
}
public static int max(int a, int b){
return (a > b)? a : b;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
String x = "BDCABA";
String y = "ABCBDAB";
getLCS(x, y);
}
}
输出结果:
手推:
最长递增子序列
package DP;
import java.util.Stack;
public class 最大递增子序列 {
public static void lis(int[] arr){
int len = arr.length;
int[] record = new int[len];
for (int i = 0; i < len; i++) {
record[i] = 1;
}
for (int i = 0; i < len; i++) {
for (int j = 0; j < i; j++) {
if(arr[i]> arr[j] && record[j]+1>record[i]){
record[i]=record[j]+1;
}
}
}
int max=0;
for (int i = 0; i < record.length; i++) {
if(record[i] > max){
max = record[i];
}
}
System.out.println("最大子序列长度为: " + max);
Stack s = new Stack();
//此处一定要从后往前查找
for (int i = len-1; i >= 0; i--) {
if(record[i] == max){
s.push(arr[i]);
max--;
}
}
while(!s.isEmpty()){
System.out.print(s.pop() + " ");
}
}
public static void main(String[] args) {
int[] arr1 = new int[]{1, 5, 8, 3, 6, 7, 2, 9};
int[] arr2 = new int[]{5,6,7,1,2,3,4,8,9};
lis(arr1);
}
}
结果:
手推:
原理:
利用动态规划思想,其实在最坏的情况下时间复杂度也是o(n*n),但是多了个差表的环节,复杂度有些情况会降低