【坐在马桶上看算法】啊哈算法13：零基础彻底弄懂"并查集"

因为最近在学并查集，在别的博客看到关于并查集的知识点，讲解得很清晰，理解更深，所以搬运到csdn来分享一下好资源。

题目描述

快过年了，犯罪分子们也开始为年终奖“奋斗”了，小哼的家乡出现了多次抢劫事件。由于强盗人数过于庞大，作案频繁，警方想查清楚到底有几个犯罪团伙实在是太不容易了，不过警察叔叔还是搜集到了一些线索，需要咱们帮忙分析一下。

现在有11个强盗。

1号强盗与2号强盗是同伙。

3号强盗与4号强盗是同伙。

5号强盗与2号强盗是同伙。

4号强盗与6号强盗是同伙。

2号强盗与6号强盗是同伙。

7号强盗与11号强盗是同伙。

8号强盗与7号强盗是同伙。

9号强盗与7号强盗是同伙。

9号强盗与11号强盗是同伙。

1号强盗与6号强盗是同伙。

有一点需要注意：强盗同伙的同伙也是同伙。你能帮助警方查出有多少个独立的犯罪团伙吗？

分析

要想解决这个问题，首先我们假设这11个强盗相互是不认识的，他们各自为政，每个人都是首领，他们只听从自己的。之后我们将通过警方提供的线索，一步步地来“合并同伙”。

第一步：我们申请一个一维数组f，我们用f[1]_{f[11]分别存储1}11号强盗中每个强盗的首领“BOSS”是谁。

第二步：初始化。根据我们之前的约定，这11个强盗最开始是各自为政的，每个强盗的BOSS就是自己。“1号强盗”的BOSS就是“1号强盗”自己，因此f[1]的值为1。以此类推，“11号强盗”的BOSS是“11号强盗”，即f[11]的值为11。请注意，这是很重要的一步。

我们用数组下标来表示强盗的编号

每个单元格中存储的是每个强盗的“BOSS”是谁

第三步：开始“合并同伙”，即如果发现目前两个强盗是同伙，则这两个强盗是同一个犯罪团伙。现在有一个问题：合并之后谁才是这个犯罪团伙的BOSS呢？

例如警方得到的第1条线索是“1号强盗与2号强盗是同伙”。“1号强盗”和“2号强盗”原来的BOSS都是自己，如今发现“1号强盗”和“2号强盗”其实是同一个犯罪团伙，那么究竟是让“1号强盗”变成“2号强盗”的BOSS，还是让“2号强盗”变成“1号强盗”的BOSS呢？一个犯罪团伙只能有一个首领。其实无所谓，都可以。我们这里假定左边的强盗更厉害一些，给这个规定起个名字叫作“靠左”法则。也就是说“2号强盗”的BOSS将变成“1号强盗”。因此我们将f[2]中的数改为1，表明“2号强盗”归顺了“1号强盗”。其实准确地说应该是原本归顺“2号强盗”的所有人都归顺了“1号强盗”才对，只不过此时“2号强盗”只孤身一人，因此只需要将f[2]的值改为1。不要着急，继续往后面看，你就知道我为什么这样说了，如下。


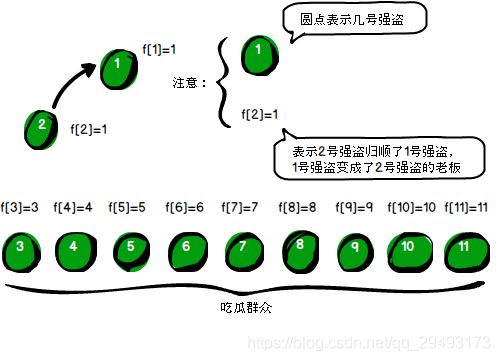
警方得到的第2条线索是“3号强盗与4号强盗是同伙”，说明“3号强盗”和“4号强盗”也是同一个犯罪团伙。根据“靠左”原则“4号强盗”归顺了“3号强盗”，所以f[4]中的值要改为3，原理和刚才处理第1条线索是一样的，如下。


警方得到的第3条线索是“5号强盗”与“2号强盗”是同伙。f[5]的值是5，说明“5号强盗”的BOSS仍然是自己。f[2]的值是1，说明“2号强盗”的BOSS是“1号强盗”。根据“靠左”法则，右边的强盗必须归顺于左边的强盗。此时你可能会将f[2]的值改为5。注意啦！此时如果你将f[2]的值改为5，就是说让“2号强盗”归顺“5号强盗”。那“1号强盗”可就不干了，你凭什么抢我的人？他非跟你干一架不可。这样会让“2号强盗”很难选择，我究竟归顺谁好呢？

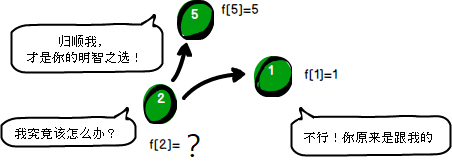
现在我来给你支个招，嘿嘿( ^_ )古语云“擒贼先擒王”。你直接找“2号强盗”的BOSS“1号强盗”谈，让其归顺“5号强盗”就OK了，也就是将f[1]的值改为5。现在“2号强盗”的BOSS是“1号强盗”，而“1号强盗”的BOSS变成了“5号强盗”，即“1号强盗”带领手下“2号强盗”归顺了“5号强盗”，这样所有的关系信息就都保留下来了。如下。


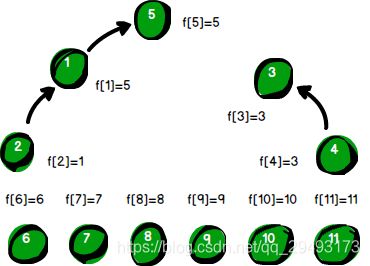
警方得到的第4条线索是“4号强盗”与“6号强盗”是同伙。f[4]的值是3，f[6]的值是6。根据“靠左”原则，让“6号强盗”加入“3号犯罪团伙”。我们需要将f[6]的值改为3。原理和处理第1条和第2条线索相同。


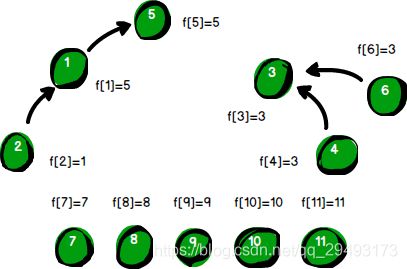
警方得到的第5条线索是“2号强盗”与“6号强盗”是同伙。f[2]的值是1，f[1]的值是5，即“2号强盗”的大BOSS（首领）是“5号强盗”。f[6]的值是3，即“6号强盗”的BOSS是“3号强盗”。根据“靠左”原则和“擒贼先擒王”原则，让“6号强盗”的BOSS“3号强盗”归顺“2号强盗”的大BOSS（首领）“5号强盗”。因此我们需要将f[3]的值改为5，即让“3号强盗”带领其手下归顺“5号强盗”。

需要特别注意的是，此时，“5号强盗”团伙内部发生了一些变动。我们在寻找“2号强盗”的大BOSS（首领）是谁时，顺带将f[2]从1改成了5，也就是说现在“2号强盗”也变成大BOSS（首领）“5号强盗”的直属手下了。

这就是强盗团伙的江湖规矩，谁能找到自己帮派的大BOSS（首领），谁就会被大BOSS（首领）提拔，升职加薪，成为大BOSS（首领）的直属手下。这种扁平化管理的方式可以有效地提高强盗团伙找大BOSS的效率，在“并查集”算法中有一个专门的术语，叫作“路径压缩”，具体代码在后面展示。


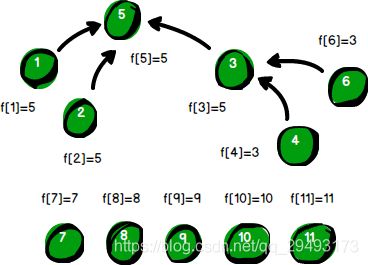
细心的同学会问了，刚才不是说如果直接把f[2]改成5，“2号强盗”和“1号强盗”之间的关系就断了吗？此一时，彼一时。在得到第3条线索的时候，那时候“1号强盗”和“5号强盗”的关系还没有建立起来，如果把f[2]改为5，“2号强盗”想要找 “1号强盗”就找不到了。但到了第5条线索的时候，“2号强盗”和“1号强盗”已经都在大BOSS（首领）“5号强盗”手下工作了，这时候将f[2]改为5，“2号强盗”想找大BOSS（首领）“5号强盗”变得更加方便，而“1号强盗”和“2号强盗”之间的关系也没有丢失，因此整体上效率变得更高了。

警方得到的第6条线索是“7号强盗”与“11号强盗”是同伙。f[11]的值是11，f[7]的值是7。根据“靠左”原则，让“11号强盗”归顺“7号强盗”。我们需要将f[11]的值改为7。


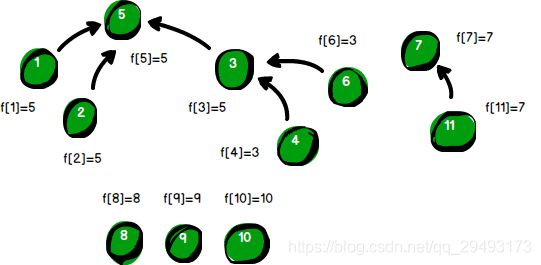
警方得到的第7条线索是“8号强盗”与“7号强盗”是同伙。f[8]的值是8，f[7]的值是7。根据“靠左”原则，让“7号强盗”归顺“8号强盗”。我们需要将f[7]的值改为8。


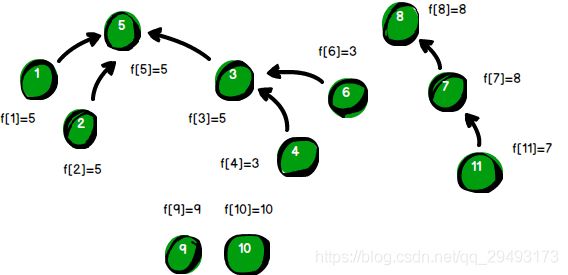
警方得到的第8条线索是“9号强盗”与“7号强盗”是同伙。f[9]的值是9，f[7]的值是8。根据“靠左”原则和“擒贼先擒王”原则，我们需要将f[8]的值改为9。


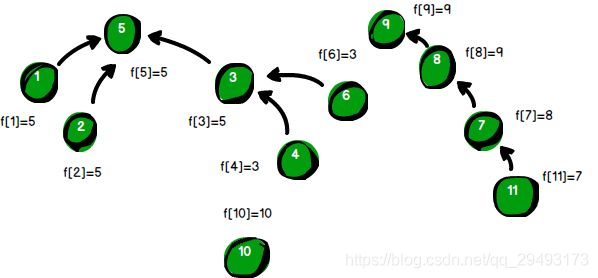
警方得到的第9条线索是“9号强盗”与“11号强盗”是同伙。f[9]的值是9，f[11]的值是7。什么？他们竟然不在同一个犯罪团伙中？这貌似不对吧，通过上图可以很显然地看出来“11号强盗”和“9号强盗”都在同一个犯罪团伙中。不过“11号强盗”并不直属于大BOSS（首领）“9号强盗”，而是归顺在“7号强盗”的手下。现在来看看“7号强盗”又归顺了谁呢？我们发现f[7]=8，也就是说“7号强盗”归顺了“8号强盗”。而f[8]=9，也就是说“8号强盗”归顺了“9号强盗”。我们再来看看“9号强盗”有没有归顺于别的人。发现f[9]的值还是9，太牛了！说明“9号强盗”的BOSS仍然是自己，他就是所在团伙的大BOSS（首领）。

我们刚才模拟的过程其实就是递归的过程。从“11号强盗”顺藤摸瓜一直找到他所在团伙的大BOSS（首领）“9号强盗”。刚才说了，强盗团伙的江湖规矩是，谁能找到自己帮派的大BOSS（首领），就会被提拔为首领的直属手下。经过这一次“路径压缩”，一路上“11号强盗”“7号强盗”和“8号强盗”，都找到了自己的大BOSS“9号强盗”。下次再问他们的BOSS是谁的时候，他们就能马上回答出是“9号强盗”啦。


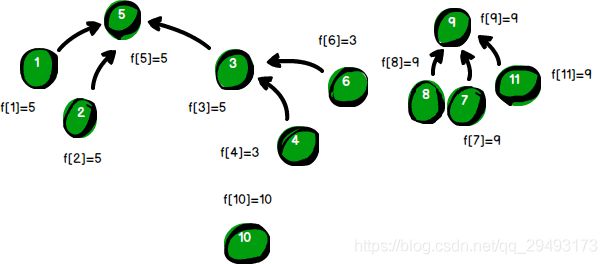
警方得到的最后一条线索是“1号强盗”与“6号强盗”是同伙。这又是一次“路径压缩”的过程。f[1]是5，“1号强盗”的BOSS是“5号强盗”。f[6]是3，“6号强盗”的BOSS是“3号强盗”。f[3]是5，“3号强盗”的BOSS是“5号强盗”。说明“6号强盗”和“1号强盗”是在一个团伙中的，但他现在并不是直接跟着团伙的大BOSS（首领）“5号强盗”，而是跟着“3号强盗”。而经过这次“路径压缩”，他的BOSS就改成了“5号强盗”。但是注意，这一次的“路径压缩”只发生在“6号强盗”“3号强盗”“5号强盗”这条路径上，团伙中的“4号强盗”不在被压缩的路径上，所以他的BOSS暂时不会改变，还是“3号强盗”。


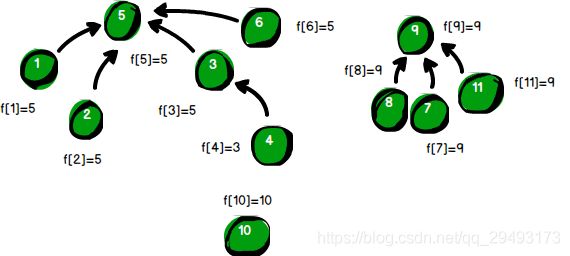
好了，所有的线索分析完毕，那么究竟有多少个犯罪团伙呢？我想你从上面的图中一眼就可以看出来了，一共有3个犯罪团伙，分别是5号犯罪团伙（由5、1、2、3、4、6号强盗组成），9号犯罪团伙（由9、8、7、11号强盗组成）以及10号犯罪团伙（只有10号强盗一个人）。从下面这张图就可以清晰地看出，如果f[i]=i，就表示此人是一个犯罪团伙的最高领导人，有多少个最高领导人就是有多少个“独立的犯罪团伙”。最后数组中f[5]=5、f[9]=9、f[10]=10，因此有3个独立的犯罪团伙。

我们刚才模拟的过程其实就是并查集的算法。并查集通过一个一维数组来实现，其本质是维护一个森林。刚开始的时候，森林的每个点都是孤立的，也可以理解为每个点就是一棵只有一个结点的树，之后通过一些条件，逐渐将这些树合并成一棵大树。其实合并的过程就是“认爹”的过程。在“认爹”的过程中，要遵守“靠左”原则和“擒贼先擒王”原则。在每次判断两个结点是否已经在同一棵树中的时候（一棵树其实就是一个集合），也要注意必须求其根源，中间父亲结点（“小BOSS”）是不能说明问题的，必须找到其祖宗（树的根结点），判断两个结点的祖宗是否是同一个根结点才行。下面我将“解密犯罪团伙”这个问题模型化，并给出代码和注释：

#include <stdio.h>   

int f[1001]={0},n,m,sum=0;   

//这里是初始化，非常地重要，数组里面存的是自己数组下标的编号就好了。   

void init()   

{   

    int i;   

    for(i=1;i<=n;i++)   

        f[i]=i;   

    return;

}   

//这是找爹的递归函数，不停地去找爹，直到找到祖宗为止，其实就是去找犯罪团伙的最高领导人，

//“擒贼先擒王”原则。

int getf(int v) {   
    if(f[v]==v)   
        return v;   
    else  {   
        //这里是路径压缩，每次在函数返回的时候，顺带把路上遇到的人的“BOSS”改为最后找
        //到的祖宗编号，也就是犯罪团伙的最高领导人编号。这样可以提高今后找到犯罪团伙的
        //最高领导人（其实就是树的祖先）的速度。
        f[v]=getf(f[v]);//这里进行了路径压缩
        return f[v];   
    } 
}   

//这里是合并两子集合的函数
void merge(int v,int u) {   
    int t1,t2;//t1、t2分别为v和u的大BOSS（首领），每次双方的会谈都必须是各自最高领导人才行
    t1=getf(v);
    t2=getf(u);
    if( t1!=t2 ) //判断两个结点是否在同一个集合中，即是否为同一个祖先。
    {  
        f[t2]=t1;
             //“靠左”原则，左边变成右边的BOSS。即把右边的集合，作为左边集合的子集合。
    }
    return;
}   

  
//请从此处开始阅读程序，从主函数开始阅读程序是一个好习惯。

int main()   {     
    int i,x,y;   
    scanf("%d %d",&n,&m);   
    init();  //初始化是必须的 
    for(i=1;i<=m;i++) {   
        //开始合并犯罪团伙   
        scanf("%d %d",&x,&y);   
        merge(x,y);   
    }
    //最后扫描有多少个独立的犯罪团伙
    for(i=1;i<=n;i++) {
        if(f[i]==i)
            sum++;
    }
    printf("%d\n",sum);
    getchar();getchar();
    return 0;   
} 

可以输入以下数据进行验证。
第一行n m，n表示强盗的人数，m表示警方搜集到的m条线索。
接下来的m行每一行有两个数a和b，表示强盗a和强盗b是同伙。

11 10
1 2
3 4
5 2
4 6
2 6
7 11
8 7
9 7
9 11
1 6
运行结果是：
3

并查集也称为不相交集数据结构。此算法的发展经历了十多年，研究它的人也很多，其中Robert E. Tarjan做出了很大的贡献。在此之前John E. Hopcroft和Jeffrey D. Ullman也进行了大量的分析。你是不是又感觉Robert E. Tarjan和John E. Hopcroft很熟悉？没错，就是发明了深度优先搜索的两个人——1986年的图灵奖得主。你看牛人们从来都不闲着的。他们到处交流，寻找合作伙伴，一起改变世界。

好了，到了本章结尾的部分啦。其实树还有很多神奇的用法，比如：线段树、树状数组、Trie树（字典树）、二叉搜索树、红黑树（是一种平衡二叉搜索树）等等。这些数据结构较为复杂，感兴趣的同学可以参考其他资料，或等待下一本《啊哈！算法2——伟大思维闪耀时》哈哈。

零基础彻底弄懂"并查集"

(出处: 啊哈磊_编程从这里起步)