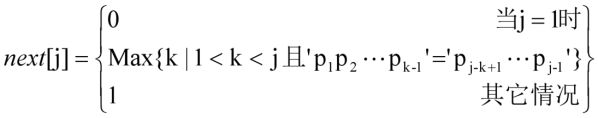4-2 串练习题
1.在字符串模式匹配的KMP算法中,求模式的next数组值得定义如下:
(1)当j=1时,为什么要取next[1]=0?
当模式串中第一个字符与主串中某字符比较不等(失配)时,next[1]=0表示模式串中已经没有字符可与主串中当前字符s[i]比较,主串当前指针应向后移至下一字符,再和模式串中第一个字符进行比较。
(2)为什么要取Max{K},K的最大值是多少?
当主串中第i个字符和模式串中的第j个字符失配时,若主串i不回溯,假定模式串的第k个字符与主串的第i个字符继续进行比较,则k应满足条件1
(3)其他情况是什么情况,为什么取next[j]=1?
以上两种情况以外的情况。主串和模式串比较失配,主串指针i不回溯,在最坏的情况下模式串从第一个字符开始和主串第i个字符进行比较,以便防止丢失可能的匹配。
2.设字符串S='aabaabaabaac',P='aabaac'
(1)给出S和P的next数组。(以表格形式给出)
| j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 模式串 |
a |
a |
b |
a |
a |
b |
a |
a |
b |
a |
a |
c |
| next[j] |
0 |
1 |
2 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| j |
1 |
2 |
3 |
4 |
5 |
6 |
| 模式串 |
a |
a |
b |
a |
a |
c |
| next[j] |
0 |
1 |
2 |
1 |
2 |
3 |
拓展:
位序 1 2 3 4 5 6 7 8 9
模式串 a b a a b c a b c
next值 0 1 1 2 2 3 1 2 3
next数组的求解方法是:
1.第一位的next值为0
2.第二位的next值为1
后面求解每一位的next值时,根据前一位进行比较
3.第三位的next值:第二位的模式串为b ,对应的next值为1;将第二位的模式串b与第一位的模式串a进行比较,不相等;则第三位的next值为1(其他情况均为1)
4.第四位的next值:第三位的模式串为a ,对应的next值为1;将第三位的模式串a与第一位的模式串a进行比较,相同,则第四位的next值得为1+1=2
5.第五位的next值:第四位的模式串为a,对应的next值为2;将第四位的模式串a与第二位的模式串b进行比较,不相等;第二位的b对应的next值为1,则将第四位的模式串a与第一位的模式串a进行比较,相同,则第五位的next的值为1+1=2
6.第六位的next值:第五位的模式串为b,对应的next值为2;将第五位的模式串b与第二位的模式中b进行比较,相同,则第六位的next值为2+1=3
7.第七位的next值:第六位的模式串为c,对应的next值为3;将第六位的模式串c与第三位的模式串a进行比较,不相等;第三位的a对应的next值为1,
则将第六位的模式串c与第一位的模式串a进行比较,不相同,则第七位的next值为1(其他情况)
8.第八位的next值:第七位的模式串为a,对应的next值为1;将第七位的模式串a与第一位的模式串a进行比较,相同,则第八位的next值为1+1=2
9.第八位的next值:第八位的模式串为b,对应的next值为2;将第八位的模式串b与第二位的模式串b进行比较,相同,则第九位的next值为2+1=3
| j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 模式串 |
a |
b |
a |
a |
b |
c |
a |
c |
| Next |
0 |
1 |
1 |
2 |
2 |
3 |
1 |
2 |
| Nextval |
0 |
1 |
0 |
2 |
1 |
3 |
0 |
2
|
1.第一位的nextval值必定为0,第二位如果于第一位相同则为0,如果不同则为1。
2.第三位的next值为1,那么将第三位和第一位进行比较,均为a,相同,则,第三位的nextval值为0。
3.第四位的next值为2,那么将第四位和第二位进行比较,不同,则第四位的nextval值为其next值,为2。
4.第五位的next值为2,那么将第五位和第二位进行比较,相同,第二位的next值为1,则继续将第二位与第一位进行比较,不同,则第五位的nextval值为第二位的next值,为1。
5.第六位的next值为3,那么将第六位和第三位进行比较,不同,则第六位的nextval值为其next值,为3。
6.第七位的next值为1,那么将第七位和第一位进行比较,相同,则第七位的nextval值为0。
7.第八位的next值为2,那么将第八位和第二位进行比较,不同,则第八位的nextval值为其next值,为2。
| j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 模式串 |
a |
b |
a |
a |
b |
c |
a |
c |
| Next[j] |
0 |
1 |
1 |
2 |
2 |
3 |
1 |
2
|
(2)若S做主串,P做模式串,试着给出利用KMP算法给出匹配的过程
3.假设以堆分配存储结构表示串,试编写将串T插入到串S中第pos个字符之前的算法。
函数原型:Status StrInsert(HString *S,int pos,HString T)
Status StrInsert(HString *S, int pos, HString T)
{
int i;
if(pos < 1 || pos > S->length + 1)
return ERROR;
if(T.length)
{
S->ch = (char *)realloc (S->ch, (S->length + T.length) *
sizeof(char));
if(!S->ch)
exit(OVERFLOW);
for (i = S->length - 1; i >= pos - 1; i--)
S->ch[i + T.length] = S->ch[i];
for (i = pos-1 ; i <= pos - 2 + T.length; i++)
S->ch[i] = T.ch[i - pos + 1];
S->length += T.length;
}
return OK;
}