Luogu P1387 最大正方形

Luogu P1387 最大正方形

一道简单但有点意思的dp题。
思考历程：
emm……二维前缀和？
看了看数据范围，才100？！枚举左上角和右上角的端点……要n⁴，过得了吗？再一看，这不是正方形吗，只枚举左上角和边长就可以了啊，利用前缀和判断正方形内是否全为1即可。虽然知道这肯定不是正解，但……先过了再说。

#include
using namespace std;

int n,m;
int pre[105][105];

int main(){
	//freopen("input.txt","r",stdin);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		for(int x,j=1;j<=m;++j){
			scanf("%d",&x);
			pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+x;
		}
	for(int k=min(n,m);k>=1;--k){
		for(int i=1;i<=n-k+1;++i){
			for(int j=1;j<=m-k+1;++j){
				if(pre[i+k-1][j+k-1]-pre[i-1][j+k-1]-pre[i+k-1][j-1]+pre[i-1][j-1]==k*k){
					printf("%d",k);
					return 0;
				}
			}
		}
	}	
	return 0;
}

看了看题解，是枚举右下角的点，f[i][j]表示以坐标 （i,j） 的点为右下角的正方形最大边长。我灵光一闪：

对于f[i][j]，它与f[i-1][j]、f[i][j-1] 有关，而当二者不等时，f[i][j] 取 min(f[i-1][j],f[i][j-1])+1。

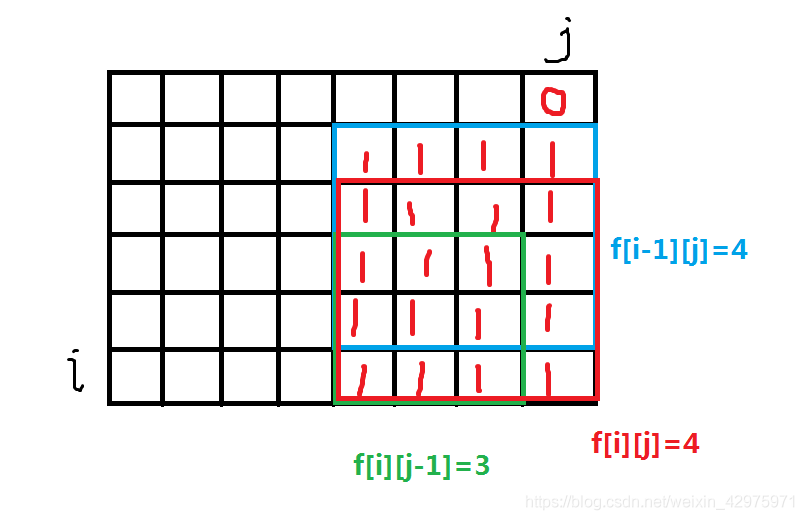
否则，若左上角的那个格子（即灰色圆圈处）为0，f[i][j] 即为 f[i-1][j]（或f[i][j-1]），否则为二者任意一个加上 1。

#include
using namespace std;

int n,m,ans;
int f[105][105],w[105][105];

int main(){
	//freopen("input.txt","r",stdin);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		for(int x,j=1;j<=m;++j){
			scanf("%d",&w[i][j]);
			if(!w[i][j]) continue;
			x=min(f[i-1][j],f[i][j-1]);
			if(w[i-x][j-x]) f[i][j]=x+1;
			else f[i][j]=max(x,1);
			ans=max(ans,f[i][j]);
		}
	printf("%d",ans);
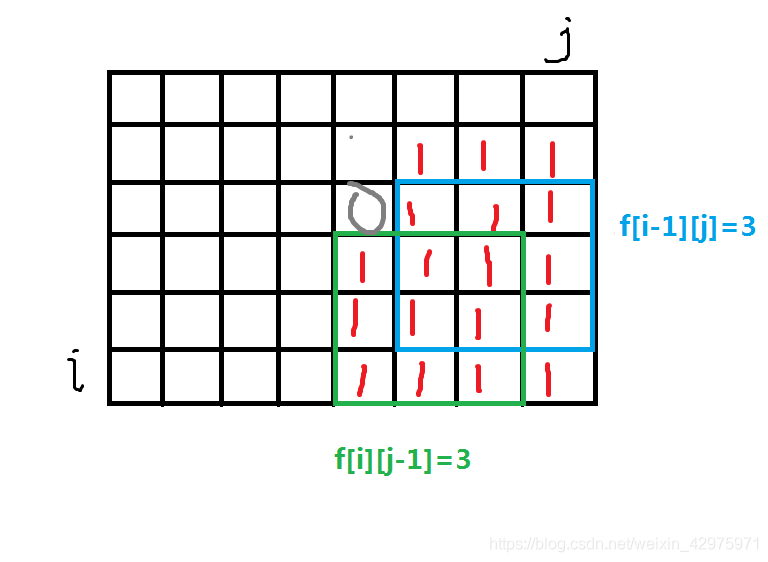
	return 0;
}

这是在我看了题解的状态设计后自己想到的。而题解的方法稍有不同，也更加简单。它的状态转移方程是

f[i][j]=min(min(f[i][j-1],f[i-1][j]),f[i-1][j-1])+1。

理解起来比较简单，暂不赘述。