暑假篇——NOIP2017模拟赛题解
目录
一.优雅的序列
1.题目
2.题解
3.Code
二.甲虫入侵
1.题目
2.题解
3.Code
三.大逃亡
1.题目
2.题解
3.Code
谢谢!
虽然三道题上了200,但还是有点菜
一.优雅的序列
1.题目
点击打开链接
2.题解
这道题难就难在重复的数字上,如果没有重复的数字,直接n-1。
不难发现,越小的数越要往前面放,但是又为了尽量避免重复,我们就轮换着放,比如:
1 1 1 2 3 4 4 4 5
就应该变成:
1 2 3 4 5 1 4 1 4
这样就能保证有最多对a[i] < a[i + 1];
具体实践如下:
step1:把每个数字排序后的起点和重复数量存在一个pair数组内;
step2:用len表示最后排好的数组长度,每次枚举每一个数字,直到枚举完每一个数字为止。
step3:统计满足条件的i的个数。
3.Code
#include
#include
#include
#include
using namespace std;
#define LL long long
int n, k, len;
LL a[100005], ans, a1[100005];
pair p[100005];
int main (){
//freopen ("grace.in", "r", stdin);
//freopen ("grace.out", "w", stdout);
scanf ("%d", &n);
for (register int i = 1; i <= n; i ++)
scanf ("%lld", &a[i]);
sort (a + 1, a + 1 + n);
for (register int i = 2; i <= n; i ++){
if (a[i] == a[i - 1]){
int j;
for (j = i; j <= n; j ++)
if (a[j] != a[j - 1])
break;
p[++ k].first = i - 1;
p[k].second = j - i + 1;
i = j;
}
else{
p[++ k].first = i - 1;
p[k].second = 1;
}
}
if (a[n] != a[n - 1]){
p[++ k].first = n;
p[k].second = 1;
}
while (len < n){
for (register int i = 1; i <= k; i ++){
if (p[i].second){
a1[++ len] = a[p[i].first];
p[i].first ++;
p[i].second --;
}
}
}
for (register int i = 1; i <= len; i ++)
if (a1[i] < a1[i + 1])
ans ++;
printf ("%lld\n", ans);
return 0;
} 二.甲虫入侵
1.题目
点击打开链接
2.题解
这道题是整个最难的题目,要用离散化+暴力搜索。
首先输入时可以把每次移动看做一个点,起点是(0,0)例如:样例第一个就是:(8,0)
每次移动要存入两个点,这是为后面的离散化做准备的;
然后,对于我们存入的每一个点,我们要进行去重操作(里面要排序),横坐标和纵坐标分别进行。
接着就进行离散化,我存入的每一个点都对应他们自己的一个下标,就可以用这些下标表示他们的值,一共只有1000个点,离散化之后整个的空间就变成了2000。
然后再来标记农夫走过的田地,这里我们用upper_bound找到农夫每次走之后的坐标离散化之后的下标,把洒过农药的田地标为1。
接着暴力搜索一波,把甲虫能到的位置标为-1;
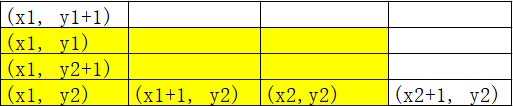
最后就是统计面积,我们先来看一看离散化之后农场的样子:(标黄的是我们要求的不被甲虫侵犯的面积)
相当于每一个点都被我扩散成了两个点,那么面积的求法就是1 * 4 + (x2 - x1 - 1) * (y1 - y2 + 1) + (y1 - y2 - 1) * (x2 - x1 + 1);
就这样求面积就完了。
有点懵,上代码:
3.Code
#include
#include
#include
#include
using namespace std;
#define LL long long
#define M 2005
int n, len[M], cntx, cnty, curx, cury, realx[M], realy[M], vis[M][M];
char dir[M];
int d[4][2] = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};
LL ans;
void unique (int *x, int &cnt){
sort (x, x + cnt);
int cnt1 = 1;
for (int i = 1; i < cnt; i ++)
if (x[i] != x[i - 1])
x[cnt1 ++] = x[i];
cnt = cnt1;
}
bool pd (int tox, int toy){
if (tox < 0 || tox >= cntx || toy < 0 || toy >= cnty || vis[tox][toy])
return 0;
return 1;
}
void DFS (int x, int y){
vis[x][y] = -1;
for (int i = 0; i < 4; i ++){
int tox = x + d[i][0];
int toy = y + d[i][1];
if (pd (tox, toy))
DFS (tox, toy);
}
}
int main (){
scanf ("%d", &n);
for (int i = 1; i <= n; i ++){
scanf ("\n%c %d", &dir[i], &len[i]);
if (dir[i] == 'L'){
realx[cntx ++] = curx + 1;
realy[cnty ++] = cury;
realx[cntx ++] = curx -= len[i];
realy[cnty ++] = cury + 1;
}
if (dir[i] == 'R'){
realx[cntx ++] = curx;
realy[cnty ++] = cury;
realx[cntx ++] = (curx += len[i]) + 1;
realy[cnty ++] = cury + 1;
}
if (dir[i] == 'U'){
realx[cntx ++] = curx;
realy[cnty ++] = cury;
realx[cntx ++] = curx + 1;
realy[cnty ++] = (cury += len[i]) + 1;
}
if (dir[i] == 'D'){
realx[cntx ++] = curx;
realy[cnty ++] = cury + 1;
realx[cntx ++] = curx + 1;
realy[cnty ++] = cury -= len[i];
}
}
unique (realx, cntx);
unique (realy, cnty);
int Indexx = lower_bound (realx, realx + cntx, curx = 0) - realx,
Indexy = lower_bound (realy, realy + cnty, cury = 0) - realy,
now;
for (int i = 1; i <= n; i ++){
if (dir[i] == 'L'){
now = lower_bound (realx, realx + cntx, curx -= len[i]) - realx;
for ( ; Indexx > now; Indexx --)
vis[Indexx][Indexy] = 1;
}
if (dir[i] == 'R'){
now = lower_bound (realx, realx + cntx, curx += len[i]) - realx;
for ( ; Indexx < now; Indexx ++)
vis[Indexx][Indexy] = 1;
}
if (dir[i] == 'U'){
now = lower_bound (realy, realy + cnty, cury += len[i]) - realy;
for ( ; Indexy < now; Indexy ++)
vis[Indexx][Indexy] = 1;
}
if (dir[i] == 'D'){
now = lower_bound (realy, realy + cnty, cury -= len[i]) - realy;
for ( ; Indexy > now; Indexy --)
vis[Indexx][Indexy] = 1;
}
}
vis[Indexx][Indexy] = 1;
for (int i = 0; i <= cntx; i ++){
if (! vis[i][0]) DFS (i, 0);
if (! vis[i][cnty]) DFS (i, cnty);
}
for (int i = 1; i < cnty; i ++){
if (! vis[0][i]) DFS (0, i);
if (! vis[cntx][i]) DFS (cntx, i);
}
for (int i = 1; i <= cntx; i ++){
for (int j = 1; j <= cnty; j ++){
if (~vis[i][j])
ans += (LL) (realx[i] - realx[i - 1]) * (realy[j] - realy[j - 1]);
}
}
printf ("%lld\n", ans);
return 0;
}
三.大逃亡
1.题目
点击打开链接
2.题解
很简单,因为答案具有单调性,直接二分答案,然后暴力搜索检查答案,注意有细节,特别是二分和距离有可能是0
3.Code
#include
#include
#include
#include
using namespace std;
#define M 10005
struct node {
int xx, yy, step;
node (){};
node (int XX, int YY, int STEP){
xx = XX;
yy = YY;
step = STEP;
}
};
int n, X, Y, sx, sy, tx, ty, dx[M], dy[M], ans1, ans2, dis[1005][1005];
int dir[4][2] = {{1, 0}, {0, -1}, {-1, 0}, {0, 1}};
bool flag[1005][1005], vis[1005][1005];
int fabs (int x){
if (x < 0)
return -x;
return x;
}
bool pd1 (int tox, int toy){
if (tox < 0 || tox >= X || toy < 0 || toy >= Y || vis[tox][toy])
return 0;
return 1;
}
void prepare (){
queue Q;
for (int i = 1; i <= n; i ++)
Q.push (node (dx[i], dy[i], 0));
while (! Q.empty ()){
node f = Q.front ();
if (! dis[f.xx][f.yy])
dis[f.xx][f.yy] = f.step;
Q.pop ();
for (int i = 0; i < 4; i ++){
int tox = f.xx + dir[i][0];
int toy = f.yy + dir[i][1];
if (pd1 (tox, toy)){
vis[tox][toy] = 1;
Q.push (node (tox, toy, f.step + 1));
}
}
}
}
bool pd (int tox, int toy, int now){
if (tox < 0 || tox >= X || toy < 0 || toy >= Y || vis[tox][toy] || dis[tox][toy] < now)
return 0;
return 1;
}
inline int BFS (int now){
memset (vis, 0, sizeof vis);
queue Q;
vis[sx][sy] = 1;
Q.push (node (sx, sy, 0));
while (! Q.empty ()){
node f = Q.front ();
Q.pop ();
if (f.xx == tx && f.yy == ty)
return f.step;
for (register int i = 0; i < 4; i ++){
int tox = f.xx + dir[i][0];
int toy = f.yy + dir[i][1];
if (pd (tox, toy, now)){
vis[tox][toy] = 1;
Q.push (node (tox, toy, f.step + 1));
}
}
}
return -1;
}
inline int check (int now){
int tmp = BFS (now);
return tmp;
}
int main (){
//freopen ("escape.in", "r", stdin);
//freopen ("escape.out", "w", stdout);
int l = 0, r = 0x3f3f3f3f, mid;
scanf ("%d %d %d %d %d %d %d", &n, &X, &Y, &sx, &sy, &tx, &ty);
for (register int i = 1; i <= n; i ++){
scanf ("%d %d", &dx[i], &dy[i]);
r = min (r, fabs (dx[i] - sx) + fabs (dy[i] - sy));
r = min (r, fabs (dx[i] - tx) + fabs (dy[i] - ty));
}
prepare ();
int tmp;
while (l + 1 < r){
mid = (l + r) / 2;
tmp = check (mid);
if (tmp != -1){
l = mid;
}
else
r = mid - 1;
}
ans1 = l, ans2 = tmp;
int tp = check (r);
if (tp != -1)
ans1 = r, ans2 = tmp;
printf ("%d %d\n", ans1, ans2);
return 0;
}