青蛙过河(递归)
本文来自于学校老师的课件,无来源地址。
青蛙过河
Time Limit: 1000 ms Memory Limit: 65536 KiB
Submit Statistic
Problem Description
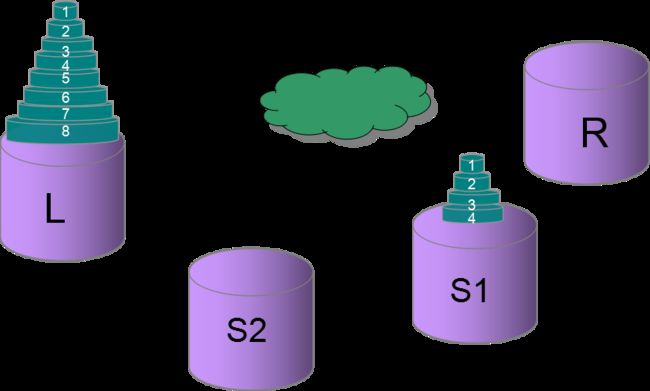
1)一条小溪尺寸不大,青蛙可以从左岸跳到右岸,在左岸有一石柱L,石柱L面积只容得下一只青蛙落脚,同样右岸也有一石柱R,石柱R面积也只容得下一只青蛙落脚。 2)有一队青蛙从小到大编号:1,2,…,n。 3)初始时:青蛙只能趴在左岸的石头 L 上,按编号一个落一个,小的落在大的上面-----不允许大的在小的上面。 4)在小溪中有S个石柱、有y片荷叶。 5)规定:溪中的每个石柱上如果有多只青蛙也是大在下、小在上,每个荷叶只允许一只青蛙落脚。 6)对于右岸的石柱R,与左岸的石柱L一样允许多个青蛙落脚,但须一个落一个,小的在上,大的在下。 7)当青蛙从左岸的L上跳走后就不允许再跳回来;同样,从左岸L上跳至右岸R,或从溪中荷叶、溪中石柱跳至右岸R上的青蛙也不允许再离开。 问题:在已知小溪中有 s 根石柱和 y 片荷叶的情况下,最多能跳过多少只青蛙?
Input
输入数据有多组,每组占一行,每行包含2个数s(s是小溪中的石柱数目)、y(y是小溪中的荷叶数目)。(0 <= s <= 10,0 <= y <= 10),输入文件直到EOF为止!
Output
对每组输入,输出有一行,输出最多能跳过的青蛙数目。
Sample Input
0 2 1 2
Sample Output
3 6
解题思路:
化难为易分析方法: 个别到一般 分解多种因素 孤立分析每个因素
1、输入: s为河中柱子数,y为荷叶数。
2、输出:最多可跳过河的青蛙数。
3、定义函数:两个整型参数s,y,返回整数值 int Jump(int s, int y);//最多可以跳过的青蛙数
4、分析:从最简开始,通过简化问题找规律
先看简单情况:
河中没有柱子,只有荷叶
s=0,即Jump(0,y)。
分解并简化问题:
1、河中无柱子:s=0,即Jump(0,y)
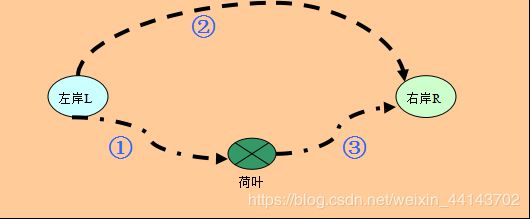
① y=1时,河中有1片荷叶,起始时L上有多只青蛙。
第一步:1# 跳到荷叶上。
第二步:2# 从L直接跳至R上。
第三步:1# 再从荷叶跳至R上。
结论:Jump(0,1)=2; // 河中有1片荷叶,能过2只青蛙
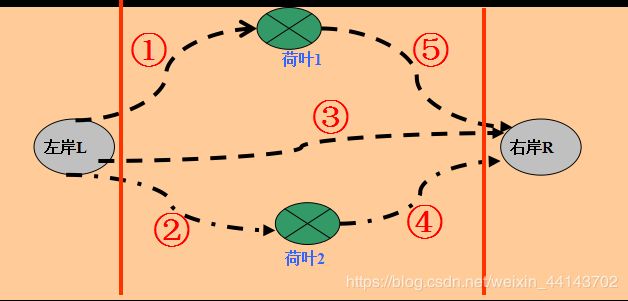
②y=2时,河中有2片荷叶时,起始时有多只青蛙落在L上。
第一步:1# 从L跳至叶 1上。
第二步:2# 从L跳至叶 2上。
第三步:3# 从L直接跳至R上。
第四步:2# 从叶2跳至R上。
第五步:1# 从叶1跳至R上。
结论: Jump(0,2)=3;// 河中有2片荷叶,能过3只青蛙
那么,请思考:
Jump(0,3)=?
Jump(0,4)=?
Jump(0,y)=?
采用归纳法:Jump(0,y)=y+1
if(s == 0)
{
return y + 1;
}
在河中没有石柱的情况下,过河的青蛙数仅取决于荷叶数,数目是荷叶数+1。
2、再看河中有石柱Jump(S, y)=?
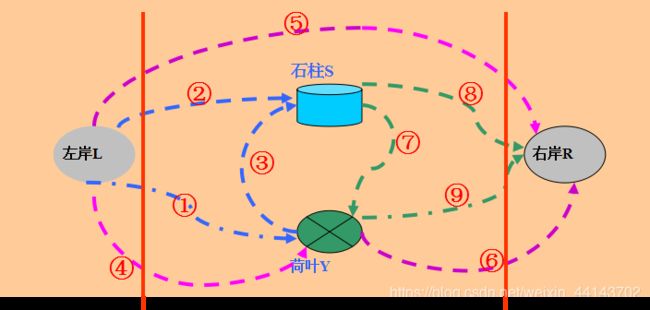
先看一个最简单情况:S=1、y=1时, 枚举(R、S、荷叶)选最优路线
1# 青蛙从 L -> Y;
2# 青蛙从 L -> S;
1# 青蛙从 Y -> S;
3# 青蛙从 L -> Y;
4# 青蛙从 L -> R;
3# 青蛙从 Y -> R;
1# 青蛙从 S -> Y;
2# 青蛙从 S -> R;
1# 青蛙从 Y -> R;
可以看出,分成2个组——关键
LYS + SYR Jump(0, 1)
LYR Jump(0, 1)
Jump(1,1) = 2 * Jump(0, 1) = 2 * 2 = 4
例如:荷叶数 y = 1、石柱数 s = 2 的 Jump(2,1)==2 * Jump(1,1) = 8
按照这样的思路
借助 s 个石柱、y 个荷叶的青蛙跳跃过程也可以推出
L(S1Y)S2 +S2(S1Y)R
L(S1Y)R
Jump(2, 1) = 2 * Jump(1, 1)
L(S1S2Y)S3 +S3(S1S2Y)R
L(S1S2Y)R
Jump(3, 1) = 2 * Jump(2, 1)
递归公式:
Jump(s, y) = 2* Jump(s-1, y)
递归结束条件:
Jump(0,y)=y+1,当s为0时
青蛙过河示例程序:
#include //声明有被调用函数
int Jump(int, int);
int main()
{
int s, y, sum;//s为河中石柱数, y为荷叶数
scanf("%d %d", &s, &y);
sum = Jump(s, y);//Jump(s,y)为被调用函数
printf("%d\n", sum);
return 0;
}
int Jump(int s, int y)//整型自定义函数, s, y为形参
{
int k; //最多跳过的青蛙数
if (s == 0) //s为0,则不再递归
{
k = y + 1;
}
else //s不为0,则递归调用
{
k = 2 * Jump(s - 1, y);
}
return k;
}
递归公式:Jump(s, y) = 2* Jump(s-1, y)
递归结束条件:Jump(0,y)=y+1,当s为0时
其他人的思路:
1. https://blog.csdn.net/a1046765624/article/details/66477361
2. https://blog.csdn.net/hfutdog/article/details/75512296
3. https://blog.csdn.net/qq_33677789/article/details/51298676