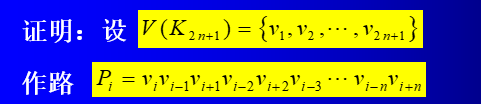电子科技大学《图论及其应用》复习总结--第五章 匹配与因子分解
第五章 匹配与因子分解
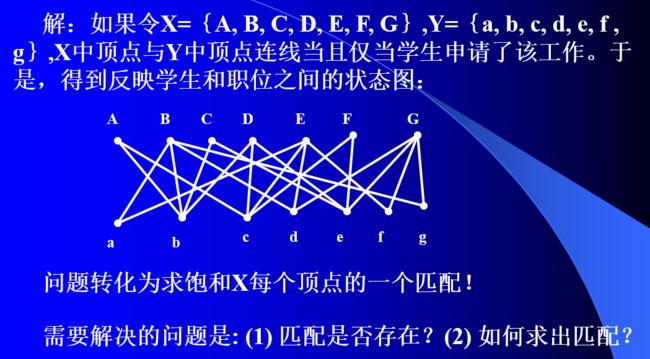
一、偶图的匹配问题
(一)、图的匹配与贝尔热定理
1、图的匹配相关概念
(1)、匹配 M— 如果M是图G的边子集(不含环),且M中的任意两条边没有共同顶点,则称M是G的一个匹配或对集或边独立集。
如果G中顶点v是G的匹配 M中某条边的端点,称它为M饱和点,否则为M非饱和点。
(2)、最大匹配 M— 如果M是图G的包含边数最多的匹配,称M是G的一个最大匹配。特别是,若最大匹配饱和了G的所有顶点,称它为G的一个完美匹配。
注:1、一个图G不一定存在完美匹配;
2、一个图G的完美匹配若存在,不一定唯一;
3、一个图G的最大匹配不一定唯一。
(3)、M交错路— 如果M是图G的匹配,G中一条由M中的边和非M中的边交错形成的路,称为G中的一条M交错路。特别地,若M交错路的起点与终点是M非饱和点,称这种M交错路为M可扩路。
2、贝尔热定理
定理1 (贝尔热,1957) G的匹配M是最大匹配,当且仅当G不包含M可扩路。
注:贝尔热定理给我们提供了扩充G的匹配的思路。
(二)、偶图的匹配与覆盖
1、问题的提出
2、偶图匹配存在性判定----Hall定理
**定理2 (Hall定理)**设G=(X, Y)是偶图,则G存在饱和X每个顶点的匹配的充要条件是:对 ∀ S ⊆ X \forall S \subseteq X ∀S⊆X,有 ∣ N ( S ) ∣ ≥ ∣ S ∣ . . . ( ∗ ) |N(S)|\geq|S|...(*) ∣N(S)∣≥∣S∣...(∗)
其中, N ( S ) N(S) N(S)表示S的邻点集
注: (1) G=(X,Y) “饱和X每个顶点的匹配”也常说成“存在由X到Y的匹配”。
(2) Hall定理也可表述为:设G=(X,Y)是偶图,如果存在X的一个子集S,使得|N(S)| < |S| ,那么G中不存在由X到Y的匹配。
(3) Hall定理也称为“婚姻定理”,表述如下:
“婚姻定理” :在一个由r个女人和s个男人构成的人群中,1≦r≦s。在熟识的男女之间可能出现r对婚姻的充分必要条件是,对每个整数k(1≦k≦r),任意k个女人共认识至少k个男人。
(4) Hall定理是在偶图中求最大匹配算法的理论基础,即匈牙利算法基础。
推论:若G是k (k>0)正则偶图,则G存在完美匹配。
(1) 证明:每个k方体都有完美匹配(k大于等于2)
k方体是k正则偶图,故存在完美匹配
(2) 求K2n和Kn,n中不同的完美匹配的个数。
K 2 n K_{2n} K2n不同的完美匹配的个数为 ( 2 n − 1 ) ! ! (2n-1)!! (2n−1)!!, K n , n K_{n,n} Kn,n不同的完美匹配的个数为 n ! n! n!
(3)证明树至多存在一个完美匹配。
证明:若不然,设M1与M2是树T的两个不同的完美匹配,那么 M 1 Δ M 2 ≠ ϕ M_1\Delta M_2 \neq \phi M1ΔM2=ϕ,且 T [ M 1 Δ M 2 ] T[M_1\Delta M_2] T[M1ΔM2]每个顶点度数为2,即它存在圈,于是推出T中有圈,矛盾。
3、点覆盖与哥尼定理
(1)、图的点覆盖概念与性质
定义1:图的点覆盖 —G的一个顶点子集K称为G的一个点覆盖,如果G的每条边都至少有一个端点在K中。G的一个包含点数最少的点覆盖称为G的最小点覆盖,其包含的点数称为G的覆盖数,记为α(G).
定理2 设M是G的匹配,K是G的覆盖,若|M|=|K|,则M是最大匹配,而G是最小覆盖。
(2)、偶图的点覆盖与偶图匹配间的关系----哥尼定理
定理2 (哥尼,1931) 在偶图中,最大匹配的边数等于最小覆盖的顶点数。
二、图的因子分解
研究图的因子分解主要是两个方面:一是能否进行分解(因子分解的存在性),二是如何分解(分解算法).
(一)、托特定理
定理 (托特定理,1947) 图G有完美匹配当且仅当对V的任意非空真子集S, 有:
o ( G − S ) ≤ ∣ S ∣ o(G-S) \leq|S| o(G−S)≤∣S∣
其中, o ( G − s ) o(G-s) o(G−s)表示奇分支数目,(奇分支是阶数为奇的连通分支)
推论 (彼得森定理) 没有割边的3正则图存在完美匹配。
注:推论中的条件是G存在完美匹配的充分条件而不是必要条件
(二)、图的一因子分解
所谓一个图G的因子 G i G_i Gi,是指至少包含G的一条边的生成子图。
所谓一个图G的因子分解,是指把图G分解为若干个边不重的因子之并。
所谓一个图G的n因子,是指图G的n度正则因子。
如果一个图G能够分解为若干n因子之并,称G是可n因子分解的。
图的一个一因子实际上就是图的一个完美匹配的导出子图。一个图能够作一因子分解,也就是它能够分解为若干边不重的完美匹配的导出子图之并。
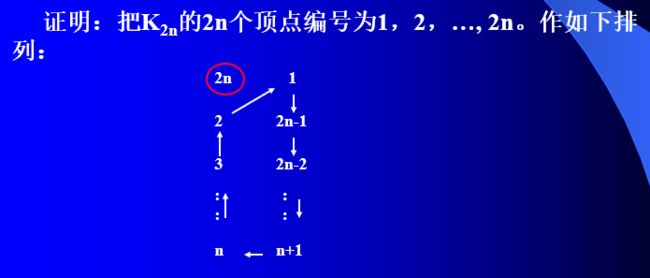
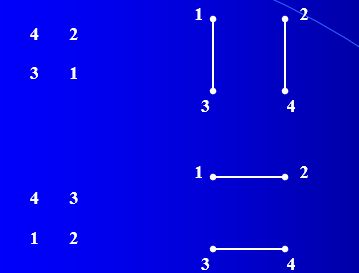
定理1 K 2 n K_{2n} K2n可一因子分解。
(作图)
例2 证明:每个k (k>0)正则偶图G是一可因子分解的。
证明:因为每个k (k>0)正则偶图G存在完美匹配,设Q是它的一个一因子,则G-Q还是正则偶图,由归纳知,G可作一因子分解。
定理2 具有H圈的三正则图可一因子分解。
证明:先从三正则图G中抽取H圈,显然剩下边构成G的一个一因子。而H圈是偶圈,它显然可以分解为两个一因子。所以G可以分解为3个一因子。
定理3 若三正则图有割边,则它不能一因子分解。
证明:若不然,设G的三个一因子为G1,G2,G3。不失一般性,设割边e∈ G1。 显然,G-G2的每个分支必然为圈。所以e在G的某个圈中,这与e是G的割边矛盾。
注:没有割边的三正则图可能也没有一因子分解,如彼得森图就是如此!尽管它存在完美匹配。
(三)、图的二因子分解
如果一个图可以分解为若干2度正则因子之并,称G可以2因子分解。注意:G的一个H圈肯定是G的一个2因子,但是G的一个2因子不一定是G的H圈。2因子可以不连通。
一个显然结论是:G能进行2因子分解,其顶点度数必然为偶数。(注意,不一定是欧拉图)
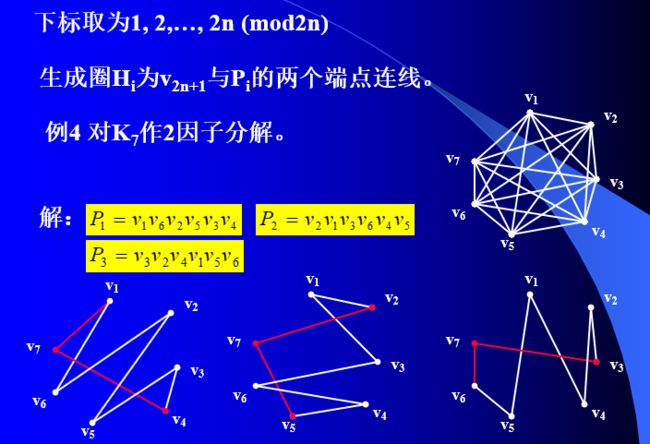
定理4 K 2 n + 1 K_{2n+1} K2n+1可因子分解。
定理5 K 2 n K_{2n} K2n可分解为一个1因子和n-1个2因子之和。
定理6 每个没有割边的3正则图是一个1因子和1个2因子之和。
定理7 一个连通图可2因子分解当且仅当它是偶数度正则图。
(四)、图的森林因子分解
把一个图分解为若干边不重的森林因子的和,称为图的森林因子分解。
三、匈牙利算法与最优匹配算法
(一)、匈牙利算法
(1)、问题
设G=(X, Y), |X|=|Y|, 在G中求一完美匹配M.
(2)、基本思想
从任一初始匹配M0出发,通过寻求一条M0可扩路P,令M1=M0ΔE§, 得到比M0更大的匹配M1(近似于迭代思想)。
M可扩路寻找方法—交错树方法
(3)、算法流程
设M是初始匹配。H是扎根于M非饱和点u的交错树。令:S=V(H)∩X, T=V(H)∩Y。
(a) 、若M饱和X所有顶点,停止。否则,设u为X中M非饱和顶点,置S={u},T=Φ;
(b) 、若N(S)=T, 则G中不存在完美匹配。否则设 y ∈N(S) – T.
(c ) 若y为M饱和点,且y z ∈M, 置S=S∪{z}, T=T∪{y},转(b)。否则,设P为M可扩路,置M1=MΔE§,转(a).
(4)、求偶图最大匹配
分析:使用匈牙利算法求完美匹配时,当在扎根于M非饱和点u的交错树上有|N(S)|<|S|时,由Hall定理,算法停止。要求出最大匹配,应该继续检查X-S是否为空,如果不为空,则检查是否在其上有M非饱和点。一直到所有M非饱和点均没有M可扩路才停止。
(二)、最优匹配算法(库恩算法)
1 、问题
设G=(X, Y)是边赋权完全偶图,且X={x1, x2,…,xn}Y={y1, y2,…,yn}, wij=w(xiyj)。在G中求出一个具有最大权值的完美匹配,称为最优匹配。
2 、可行顶点标号与相等子图
定义2 设G=(X, Y), 若对任意的x ∈X, y ∈Y,有: l ( x ) + l ( y ) ≥ w ( x y ) l(x)+l(y)\geq w(xy) l(x)+l(y)≥w(xy), 称 l 是赋权完全偶图G的可行顶点标号。
事实上,设:
{ l ( x ) = max y ∈ Y w ( x y ) , 若 x ∈ X , l ( y ) = 0 , 若 y ∈ Y \begin{cases}l(x)=\max\limits_{y\in Y}{w(xy)},若x\in X,\\l(y)=0,若y\in Y \end{cases} {l(x)=y∈Ymaxw(xy),若x∈X,l(y)=0,若y∈Y
则 l 是G的一个可行顶点标号。
定义3 设 l 是赋权完全偶图G=(X, Y)的可行顶点标号,令: E l = { x y ∈ E ( G ) ∣ l ( x ) + l ( y ) = w ( x y ) } E_l=\{ xy\in E(G)|l(x)+l(y)=w(xy)\} El={xy∈E(G)∣l(x)+l(y)=w(xy)}, 称 G l = G [ E l ] G_l=G[E_l] Gl=G[El]为G的对应于l 的相等子图。
定理 设 l 是赋权完全偶图G=(X, Y)的可行顶点标号,若相等子图 G l G_l Gl有完美匹配M*,则M*是G的最优匹配。
证明:设M*是 G l G_l Gl的完美匹配,则:
w ( M ∗ ) = ∑ e ∈ M ∗ w ( e ) = ∑ v ∈ V ( G ) l ( V ) w(M^*)=\sum_{e\in M^*}w(e)=\sum_{v\in V(G)}l(V) w(M∗)=e∈M∗∑w(e)=v∈V(G)∑l(V)
又设M是G的任一完美匹配,则:
w ( M ) = ∑ e ∈ M w ( e ) ≤ ∑ v ∈ V ( G ) l ( V ) w(M)=\sum_{e\in M}w(e)\leq\sum_{v\in V(G)}l(V) w(M)=e∈M∑w(e)≤v∈V(G)∑l(V)
所以,w (M*)≥w (M)。即M*是G的最优匹配。
3、算法思想及流程
采用顶点标号修改策略。流程如下:
给一初始顶点标号l ,在G G l G_l Gl任选一个匹配M。
(1) 若X是M饱和的,则M是最优匹配。否则,令u是一个M非饱和点,置:S={u},T=Φ。
(2) 若 N G l ( S ) ⊃ T N_{G_l}(S)\supset T NGl(S)⊃T ,转(3)。否则,计算: α l = min x ∈ S y ∉ T { l ( x ) + l ( y ) − w ( x y ) } \alpha _l=\min\limits_{x\in S\\y\notin T}\{l(x)+l(y)-w(xy)\} αl=x∈Sy∈/Tmin{l(x)+l(y)−w(xy)}
l ^ = { l ( v ) − α l , v ∈ S l ( v ) + α l , v ∈ T l ( v ) , 其 他 \hat{l}= \begin{cases}l(v)-\alpha _l,v\in S\\l(v)+\alpha _l,v\in T \\l(v), \quad 其他\end{cases} l^= ⎩⎪⎨⎪⎧l(v)−αl,v∈Sl(v)+αl,v∈Tl(v),其他
给出新的可行顶点标号,在新标号下重新开始。
(3) 在 N G l ( S ) − T N_{G_l}(S)-T NGl(S)−T中选择点y。若y是M饱和的,yz ∈M,则置S=S∪{z},T=T∪{y}转(2)。否则,设P是 G l G_l Gl中M可扩路,置M=MΔE§,转(1).
注:该算法把匈牙利算法用于其中,主要是用来判定和求完美匹配。
总结:常用符号
α ( G ) \alpha(G) α(G) 表示图 G G G的覆盖数,为G的最小点覆盖包含的点数
总结:常用性质定理
1、贝尔热定理
G的匹配M是最大匹配,当且仅当G不包含M可扩路
2、偶图匹配存在性判定----Hall定理
G=(X, Y)是偶图,则G存在饱和X每个顶点的匹配的充要条件是:
对$\forall S \subseteq X , 有 ,有 ,有|N(S)|\geq|S|…(*)$
其中, N ( S ) N(S) N(S)表示S的邻点集
3、哥尼定理
在偶图中,最大匹配的边数等于最小覆盖的顶点数
4、托特定理
图G有完美匹配当且仅当对V的任意非空真子集S, 有:
o ( G − S ) ≤ ∣ S ∣ o(G-S) \leq|S| o(G−S)≤∣S∣
其中, o ( G − s ) o(G-s) o(G−s)表示奇分支数目,(奇分支是阶数为奇的连通分支)
5、彼得森定理
没有割边的3正则图存在完美匹配
6、匈牙利算法(偶图中求完美匹配以及最大匹配)
7、库恩算法(最优匹配算法)
设G=(X, Y)是边赋权完全偶图,且X={x1, x2,…,xn}Y={y1, y2,…,yn}, wij=w(xiyj)。在G中求出一个具有最大权值的完美匹配。
方法:可行顶点标号----生成子图----匈牙利完美匹配算法----计算权值 α l = min x ∈ S y ∉ T { l ( x ) + l ( y ) − w ( x y ) } \alpha _l=\min\limits_{x\in S\\y\notin T}\{l(x)+l(y)-w(xy)\} αl=x∈Sy∈/Tmin{l(x)+l(y)−w(xy)}----更改相应可行顶 l ^ = { l ( v ) − α l , v ∈ S l ( v ) + α l , v ∈ T l ( v ) , 其 他 \hat{l}= \begin{cases}l(v)-\alpha _l,v\in S\\l(v)+\alpha _l,v\in T \\l(v), \quad 其他\end{cases} l^=⎩⎪⎨⎪⎧l(v)−αl,v∈Sl(v)+αl,v∈Tl(v),其他,重复
8、其他
定理 设 l 是赋权完全偶图G=(X, Y)的可行顶点标号,若相等子图 G l G_l Gl有完美匹配M*,则M*是G的最优匹配。
总结:一些结论
-
一个图G不一定存在完美匹配。一个图G的完美匹配若存在,不一定唯一。一个图G的最大匹配不一定唯一
-
若G是k (k>0)正则偶图,则G存在完美匹配。
-
每个k方体都有完美匹配(k大于等于2)
-
K 2 n K_{2n} K2n不同的完美匹配的个数为 ( 2 n − 1 ) ! ! (2n-1)!! (2n−1)!!, K n , n K_{n,n} Kn,n不同的完美匹配的个数为 n ! n! n!
-
树至多存在一个完美匹配
-
有完美匹配的三正则图不一定没有割边
-
三正则哈密尔顿图存在完美匹配,可1-因子分解
-
任意非平凡正则偶图包含完美匹配且能够1-因子分解
-
K 2 n K_{2n} K2n可一因子分解, K 2 n + 1 K_{2n+1} K2n+1可2因子分解, K 2 n K_{2n} K2n可分解为一个1因子和n-1个2因子之和。
-
每个没有割边的3正则图是一个1因子和1个2因子之和
-
一个连通图可2因子分解当且仅当它是偶数度正则图