现代数字信号处理第五章——维纳滤波在信号处理中的应用
主要内容
- 线性滤波器及其与AR模型的互逆关系
- 前后向线性预测;格型滤波器;Burg算法
- 信道均衡
一、线性预测
\quad 如下图所示包含M个抽头的滤波器,用 u ( n − 1 ) , u ( n − 2 ) , ⋯ , u ( n − M ) u(n-1),u(n-2),\cdots,u(n-M) u(n−1),u(n−2),⋯,u(n−M)来预测 u ( n ) u(n) u(n),称为M阶线性预测 L P ( M ) LP(M) LP(M)。
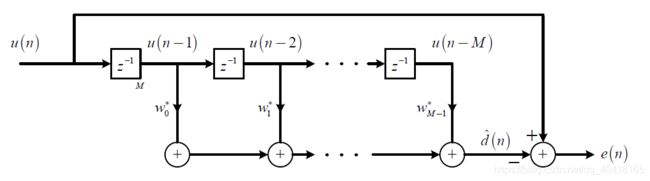
- 输入向量: u ( n ) = [ u ( n − 1 ) , u ( n − 2 ) , ⋯ , u ( n − M ) ] T u(n)=[u(n-1),u(n-2),\cdots,u(n-M)]^T u(n)=[u(n−1),u(n−2),⋯,u(n−M)]T
- 权向量: w = [ w 0 , ⋯ , w M − 1 ] T w=[w_0,\cdots,w_{M-1}]^T w=[w0,⋯,wM−1]T
- 自相关矩阵: R = E { u ( n ) u H ( n ) } R=E\{u(n)u^H(n)\} R=E{u(n)uH(n)}
- 互相关预测: p = E { u ( n ) d ∗ ( n ) } = [ r ( − 1 ) , r ( − 2 ) , ⋯ , r ( − M ) ] T p=E\{u(n)d^*(n)\}=[r(-1),r(-2),\cdots,r(-M)]^T p=E{u(n)d∗(n)}=[r(−1),r(−2),⋯,r(−M)]T
- M阶线性预测满足维纳-霍夫方程: R w 0 = p Rw_0=p Rw0=p
- 满足维纳-霍夫方程的线性预测称为最佳线性预测,简称线性预测
- J m i n = σ d 2 − p H w 0 = r ( 0 ) − w 0 r ( 1 ) − w 1 r ( 1 ) − ⋯ − w M − 1 r ( M ) J_{min}=\sigma_d^2-p^Hw_0=r(0)-w_0r(1)-w_1r(1)-\cdots-w_{M-1}r(M) Jmin=σd2−pHw0=r(0)−w0r(1)−w1r(1)−⋯−wM−1r(M)
线性预测器与AR模型的关系
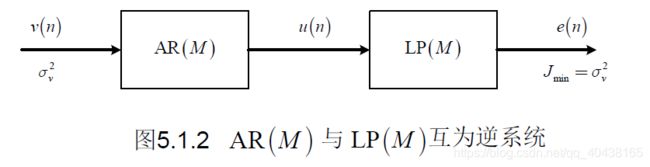
H A R ( z ) = 1 1 + a 1 z − 1 + a 2 z − 2 + ⋯ + a M z − M H L P ( z ) = 1 + a 1 z − 1 + a 2 z − 2 + ⋯ + a M z − M H A R ( z ) H L P ( z ) = 1 H_{AR}(z)=\frac{1}{1+a_1z^{-1}+a_2z^{-2}+\cdots+a_Mz^{-M}}\\H_{LP}(z)=1+a_1z^{-1}+a_2z^{-2}+\cdots+a_Mz^{-M}\\H_{AR}(z)H_{LP}(z)=1 HAR(z)=1+a1z−1+a2z−2+⋯+aMz−M1HLP(z)=1+a1z−1+a2z−2+⋯+aMz−MHAR(z)HLP(z)=1
\quad M阶LP与M阶AR互为逆袭统


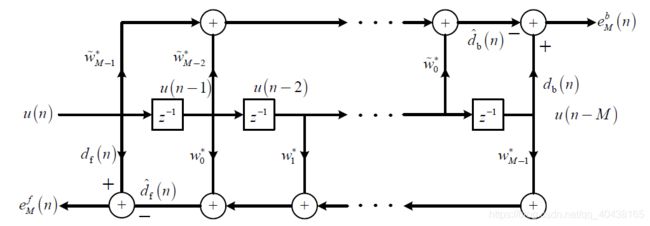
二、前后向线性预测;格型滤波器;Burg算法
1、前向线性预测FLP
- 用 u ( n − 1 ) , u ( n − 2 ) , ⋯ , u ( n − M ) u(n-1),u(n-2),\cdots,u(n-M) u(n−1),u(n−2),⋯,u(n−M)来预测 u ( n ) u(n) u(n)
- FLP的维纳霍夫方程: R w f o = p , w f o Rw_{fo}=p,w_{fo} Rwfo=p,wfo是FLP最优权向量

2、后向线性预测BLP
- 用 u ( n − M + 1 ) , u ( n − M + 2 ) , ⋯ , u ( n ) u(n-M+1),u(n-M+2),\cdots,u(n) u(n−M+1),u(n−M+2),⋯,u(n)来预测 u ( n − M ) u(n-M) u(n−M)
- FLP的维纳霍夫方程: R b w b o = p b , w b o R_bw_{bo}=p_b,w_{bo} Rbwbo=pb,wbo是BLP最优权向量

- R b = R ∗ , p b = p ∗ , w f o = w b o ∗ R_b=R^*,p_b=p^*,w_{fo}=w_{bo}^* Rb=R∗,pb=p∗,wfo=wbo∗,可见在最小均方误差下,FLP和BLP估计权向量时效果相同
- w ^ o = 1 2 ( w ^ f o + w ^ b o ) \hat{w}_{o}=\frac{1}{2}(\hat{w}_{fo}+\hat{w}_{bo}) w^o=21(w^fo+w^bo),统计意义下,估计 w ^ o \hat{w}_{o} w^o比单独进行前向或者后向预测具有更小的估计误差
3、FBLP格型滤波器
\quad 将随机过程 u ( n ) u(n) u(n)输入到格型滤波器,则可分别得到不同阶数的FBLP的最小前向预测误差 e m f ( n ) e_m^f(n) emf(n)和最小后向预测误差 e b f ( n ) e_b^f(n) ebf(n),满足下式的递推关系:


4、Burg算法
\quad 利用Burg算法可以根据N个观测样本数据估计各阶FBLP的反射系数 k m k_m km
\quad Burg算法可以估计AR(M)模型的参数,进而得到AR(M)功率谱密度的估计。
三、信道均衡
\quad 在数字通信系统中,接受信号通常会受到加性噪声;码间干扰、衰落等因素影响,要获得发射符号的可靠估计,通常需要在接收机中对接收信号进行均衡。
1、离散时间通信信道模型

s ~ ( t ) = ∑ l = − ∞ ∞ s ( l ) g ( t − l T ) u ~ ( t ) = s ~ ( t ) ∗ c ( t ) + v ~ ( t ) = ∑ l = − ∞ ∞ s ( l ) h ~ ( t − l T ) + v ~ ( t ) 其 中 h ~ ( t ) = g ( t ) ∗ c ( t ) , 对 其 采 样 , 最 终 输 入 输 出 关 系 为 u ( n ) = ∑ l = 0 L h l s ( n − l ) + v ( n ) \widetilde{s}(t)=\sum_{l=-\infty}^\infty s(l)g(t-lT)\\\widetilde{u}(t)=\widetilde{s}(t)*c(t)+\widetilde{v}(t)=\sum_{l=-\infty}^\infty s(l)\widetilde{h}(t-lT)+\widetilde{v}(t)\\其中\widetilde{h}(t)=g(t)*c(t),对其采样,最终输入输出关系为\\u(n)=\sum_{l=0}^Lh_ls(n-l)+v(n) s (t)=l=−∞∑∞s(l)g(t−lT)u (t)=s (t)∗c(t)+v (t)=l=−∞∑∞s(l)h (t−lT)+v (t)其中h (t)=g(t)∗c(t),对其采样,最终输入输出关系为u(n)=l=0∑Lhls(n−l)+v(n)
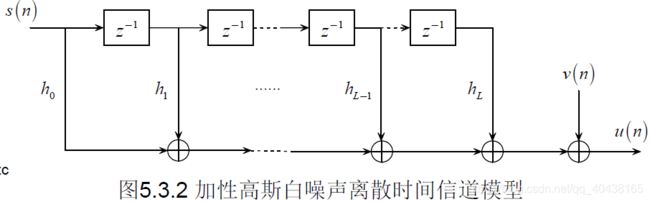
\quad 对上式展开,可得到 u ( n ) = h 0 s ( n ) + ∑ l = 1 L h l s ( n − l ) + v ( n ) u(n)=h_0s(n)+\sum_{l=1}^Lh_ls(n-l)+v(n) u(n)=h0s(n)+∑l=1Lhls(n−l)+v(n),式子第一项表示第n个采样时刻携带信息的符号,第二项表示引入码间干扰,等价模型如下图:
2、迫零滤波器
a.理想的逆滤波器

\quad 要消除码间干扰,则级联的单位冲激响应 f ( n ) f(n) f(n)应满足 f ( n ) = w ( n ) ∗ h ( n ) = ∑ k = − ∞ ∞ w k ∗ h n − k = δ ( n ) F ( z ) = W ( z ) H ( z ) = 1 均 衡 器 W ( z ) = 1 H ( z ) f(n)=w(n)*h(n)=\sum_{k=-\infty}^\infty w_k^*h_{n-k}=\delta(n)\\F(z)=W(z)H(z)=1\\均衡器W(z)=\frac{1}{H(z)} f(n)=w(n)∗h(n)=k=−∞∑∞wk∗hn−k=δ(n)F(z)=W(z)H(z)=1均衡器W(z)=H(z)1
因此,要完全消除码间干扰,均衡器 W ( z ) W(z) W(z)应该是 H ( z ) H(z) H(z)的理想逆滤波器 。称满足该条件的均衡器是迫零滤波器。
b.FIR迫零均衡器

\quad w ^ 是 F I R 滤 波 器 的 权 向 量 w ^ = [ w ^ − M , w ^ − M + 1 , ⋯ , w ^ M ] \hat{w}是FIR滤波器的权向量\hat{w}=[\hat{w}_{-M},\hat{w}_{-M+1},\cdots,\hat{w}_{M}] w^是FIR滤波器的权向量w^=[w^−M,w^−M+1,⋯,w^M],经过推导,可以得到,迫零滤波器要求权向量 w ^ \hat{w} w^满足 f d = C w ^ ∗ f d = [ 0 , ⋯ , 0 , 1 , 0 , ⋯ , 0 ] T 只 有 第 M + 1 项 不 为 0 C 是 信 道 冲 激 响 应 矩 阵 f_d=C\hat{w}^*\\f_d=[0,\cdots,0,1,0,\cdots,0]^T只有第M+1项不为0\\C是信道冲激响应矩阵 fd=Cw^∗fd=[0,⋯,0,1,0,⋯,0]T只有第M+1项不为0C是信道冲激响应矩阵
\quad 若预先得到矩阵C,则由上式可以解出均衡滤波器权向量 w ^ \hat{w} w^。
3、基于于MMSE准则的FIR均衡滤波器
\quad 均衡器输入向量 u ( n ) = H s ( n ) + v ( n ) u(n)=Hs(n)+v(n) u(n)=Hs(n)+v(n),其中 H H H是信道矩阵
- 利用最小均方误差准则,MMSE均衡器是维纳-霍夫方差的解: w ^ o = R − 1 p \hat{w}_o=R^{-1}p w^o=R−1p
- R = E { u ( n ) u H ( n ) } = E { ( H s ( n ) + v ( n ) ) ( H s ( n ) + v ( n ) ) H } = H E { s ( n ) s H ( n ) } H H + E { v ( n ) v H ( n ) } = σ s 2 H H H + σ v 2 I R=E\{u(n)u^H(n)\}=E\{(Hs(n)+v(n))(Hs(n)+v(n))^H\}=HE\{s(n)s^H(n)\}H^H+E\{v(n)v^H(n)\}=\sigma_s^2HH^H+\sigma_v^2I R=E{u(n)uH(n)}=E{(Hs(n)+v(n))(Hs(n)+v(n))H}=HE{s(n)sH(n)}HH+E{v(n)vH(n)}=σs2HHH+σv2I
- p = E { u ( n ) s ∗ ( n ) } = σ s 2 [ H ] M + 1 = σ s 2 [ h M , h M + 1 , ⋯ , h 0 , 0 ] T p=E\{u(n)s^*(n)\}=\sigma_s^2[H]_{M+1}=\sigma_s^2[h_M,h_{M+1},\cdots,h_0,0]^T p=E{u(n)s∗(n)}=σs2[H]M+1=σs2[hM,hM+1,⋯,h0,0]T
- 计算出 w ^ o \hat{w}_o w^o后,得到最小均方误差为 J m i n = σ s 2 − w ^ o H p J_{min}=\sigma_s^2-\hat{w}_o^Hp Jmin=σs2−w^oHp
- 可以看出,如果已知信道系数 { h l } l = 0 L \{h_l\}_{l=0}^L {hl}l=0L,则可直接计算出均衡滤波器的权向量