【论文笔记】Quantifying Similarity between Relations with Fact Distribution

导读

闲得无聊了，模型在运行，我要看下论文，组内同学写的，话说hao zhu师兄真是又帅又猛

Abstract

任务： 度量关系之间的相似度

方法：核心观点是通过entity pair的条件分布的divergence

这个想法是很自然而然的，因为在给定关系的情况下，entity pair肯定是符合特定分布的，打个比方：

• 三元组（Entity_A, Entity_B, is friend of) ，就限制了entity A和 entity B必须是人，一个人很少说能和电脑做朋友的吧，有也应该是分布中的极小概率事件。
• 三元组（Entity_A, Entity_B, is daughter of) ，假设B的分布与上述相同，但是A的分布必须是女性。

这就导致两种关系的entity pair的分布是不相同的，如果两个关系越相近，那么entity pair也越能够替换，因此distribution也越相似甚至完全相同。

比如【在哪个大学上学】和【在哪个大学受教育】，这俩就几乎一摸一样。

相反地，如果两个关系差别越大，那么其分布也就越多。

这里特殊提一下divergence吧，divergence按我粗浅的理解就是用来度量两个分布的方法，具体的有KL散度或者S啥的散度，在这里用的具体是KL散度，这个是关系抽取里面经常用的散度（实际上我就没见过他们用别的散度）

好，文章主要有以下一些发现：

• 方法可以减少OpenIE抽取处的过于specific的细粒度的关系，因为OpenIE是tagging-based的关系抽取，且该方法又可以用于度量关系，所以如果两个relation完全一致但是表征不同，那么可以归类于同一类关系。
• 即使最牛的模型也会把很相似的关系区分错误。
• 作者的方法引入负采样和softmax分类可以缓解这些问题。

1. Introduction

前面讲的都是熟悉的娓娓道来，此处略去不表了。

这个方法具体一点来说：

对于关系$r$, 条件分布为$P(h,t|r)$ , $h,t\in \mathcal{E}$ 是头尾entity， $r\in \mathcal{R}$是关系

所以通过给定关系$r$的情况下，度量由$h,t$组成的条件分布$P$，从而计算相似度，合情合理。

在文中，条件概率是由神经网络计算的。

大家注意这里，条件概率由网络计算，这个非常简单，网络很容易给出概率的，现在的预测都是算概率。

足够多的entity pair，被计算了足够多的概率，就可以用这些数据构成一个分布情况，然后通过分布情况来进行KL散度的计算。很好的思路。

但是这里面有一个问题：足够多是多少呢？我不能直接得到分布的，我只能通过概率去估计这个分布，那么求所有数据的概率太费时间了，文中说的是’intractable’，因此文中又提出了一个 sampling-based method

至此，本文的贡献：

1. 根据上述思路，提出了模型，构成一个框架
2. 根据框架做了非常多的研究和调查，回答以下几个问题：
   1. 计算出的相似度和人类的判断相关性如何？
   2. 如何用这个方法帮助OpenIE？
   3. 最好的模型是否依然无法判断相似关系？
   4. 能否将相似度用于某些启发式的方法中去加强关系预测的负采样？
   5. 相似度能否作为一种在softmax-margin中的自适应margin用于关系抽取？

其实这些问题不用觉得很夸张，其实只要将能够很好的度量关系之间的相似度作为前提，那么这些问题并不算太难想到。毕竟咱们组这么大呢。

让我思考了比较久的是第四和第五个问题。

4. 负采样的意思我觉得可能想表达的意思是，如果两个关系比较相似，但是的确是不同的，那么加强负例的采样，从而到达让正例识别更加准确的情况。
5. 自适应的margin，softmax-margin可能是想说明不同的relation margin不同？

很可能想错了，需要在后续的文章中才能看完全。

2. Learning Head-Tail Distribution

2.1 Formal Definition of Fact Distribution

实际数据不一定足够地反应真实的分布，那么该如何获取一个general的分布呢

设 $\mathcal{E},\mathcal{R}$是entity集合和relation集合。那么度量方程为
$$F_{\theta }:\mathcal{E}\times \mathcal{R}\times \mathcal{E}\to \mathbb{R}$$
其中的$\mathbb{R}$是一个常量

可以理解为度量出$h,t$属于$r$关系的概率。一种特殊情况：
$$F_{\theta }(h,t;r)\triangleq u_{{\theta }_1}(h;r)+u_{{\theta }_2}(t;h,r)$$
作者的意思应该是，原本要一起度量的，算了，我这边设置两套不同的参数分别学习，效果差不多的。

那么最终，对每一个三元组，计算的概率为：
$${\tilde{P}}_{\theta }(h,t\mid r)\triangleq \exp F_{\theta }(h,r;t)$$

注意，此处的概率还没有经过标准化，所以此处再经过一下标准化，同样的公式，对上述两个分别计算的概率进行标准化。
$$\begin{array}{rl}{u}_{{\theta }_1}(h;r)& =\log \frac{\exp {\tilde{u}}_{{\theta }_1}(h;r)}{{\sum }_{h^{\prime }}\exp {\tilde{u}}_{{\theta }_1}\left(h^{\prime };r\right)}\\ u_{{\theta }_2}(t;h,r)& =\log \frac{\exp {\tilde{u}}_{{\theta }_2}(t;h,r)}{{\sum }_{t^{\prime }}\exp {\tilde{u}}_{{\theta }_2}\left(t^{\prime };h,r\right)}\end{array}$$

这样之后，${\tilde{P}}_{\theta }(h,t\mid r)$就可以是有效的概率估计函数了，因为${\sum }_{h,t}\exp F_{\theta }(h,t;r)=1$。所以作者将其认为真实的采样概率。

此处标准化的公式也非常的简单，就是经过softmax之后再加了一个log，因为$u_{{\theta }_1}$需要和$u_{{\theta }_2}$相加，之后再使用exp，这样才可以满足${\sum }_{h,t}\exp F_{\theta }(h,t;r)=1$

2.2 Neural architecture design

此处不讲了，就是简单的feed-forward。激活函数是relu
$$\begin{array}{rl}{\tilde{u}}_{{\theta }_1}(h;r)& ={\mathrm{MLP}}_{{\theta }_1}(\mathbf{r}{)}^{\top }\mathbf{h}\\ {\tilde{u}}_{{\theta }_2}(t;h,r)& ={\mathrm{MLP}}_{{\theta }_2}([\mathbf{h};\mathbf{r}]{)}^{\top }\mathbf{t}\end{array}$$

2.3 Training

$$\begin{array}{rl}{\theta }^{\ast }& =\underset{\theta }{\mathrm{argmin}}\mathcal{L}(G)\\ & =\underset{\theta }{\mathrm{argmin}}\sum _{(h,r,t)\in G}-\log P_{\theta }(h,t\mid r)\end{array}$$

loss函数就是最小化的负对数似然函数， 优化器用的Adam

3. Quanifying Similarity

3.1 Relations as Distributions

训练之后，模型被期待于在整个$\mathcal{E} \times \mathcal{R} \times \mathcal{E} $ 泛化良好

3.2 Defining Similarity

作者期望条件分布-$P_{{\theta }^{\ast }}(h,t|r)$可以用于反应出关系之间的相似度。

如果两个关系之间的条件分布集中在相似的entity pairs上，两个关系就相似。（这边是基础思想，开篇我们就谈及了）

所以，具体的两个关系的相似度度量公式如下
$$\begin{array}{rl}S\left(r_1,r_2\right)=g(& D_{\mathrm{K}\mathrm{L}}\left(P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)||P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)\right)\\ & D_{\mathrm{K}\mathrm{L}}\left(P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)\Vert P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)\right))\end{array}$$

其中$D_{KL}(\cdot ||\cdot )$是KL散度，前后互换是因为KL散度并不对称。

那么该公式的计算具体又如下：（这就是纯KL的定义）

$$\begin{array}{l}{D}_{\mathrm{K}\mathrm{L}}\left(P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)\Vert P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)\right)\\ ={\mathbb{E}}_{h,t\sim P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)}\log \frac{P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)}{P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)}\end{array}$$

$g(x,y)$是用来对称的，且要满足单调递减，非负。因此$g(x,y)=e^{-max(x,y)}$

由于考虑的是双边的KL散度，所以作者同时引入了$r_1$, $r_2$的entity pair。

值得一提的是，在直觉上，如果$P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)$主要分布在$P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)$ 强调的entity pairs。那么$r_1$就是$r_2$的hyponymy（下位关系，lexical taxonomy里面可以翻译为下义词）。也就是$r_1$ is a $r_2$, $r_1$被$r_2$全包围了

比方说$r_1$是父亲关系，$r_2$就可以是 亲戚关系。那么父亲是一种亲戚。

同时考虑双边的KL散度，可以带来更加丰富和全面的考虑。

3.3 Calculating Similarity

在Introduction中所说的，计算相似度非常复杂，计算复杂度为$\mathcal{O}({\mathcal{E}}^2)$，因此作者采用模特卡洛估计：
$$\begin{array}{rl}& D_{\mathrm{K}\mathrm{L}}\left(P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)\Vert P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)\right)\\ =& {\mathbb{E}}_{h,t\sim P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)}\log \frac{P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)}{P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)}\\ =& \frac{1}{|\mathcal{S}|}\sum _{h,t\in \mathcal{S}}\log \frac{P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)}{P_{{\theta }^{\ast }}\left(h,t\mid r_2\right)}\end{array}$$
重点主要是$\mathcal{S}$，为从$P_{{\theta }^{\ast }}\left(h,t\mid r_1\right)$ entity pairs的列表，

采样方法使用顺序方法去获得$\mathcal{S}$，也就是先采样$h$再采样$t$，这样时间就变成线性的了, 为$\mathcal{O}(\mathcal{E})$

3.4 Relationship with other metrics

现有的方法主要是将关系表征成响亮，矩阵，或者角度。

使用概率分布来度量相似度的主要好处有两个：

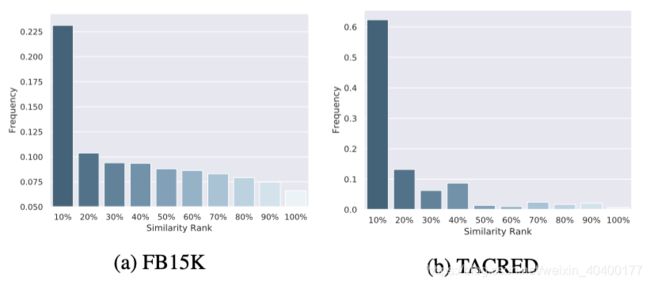
1. 其他表征成为固定长度的representation，他的表征性能是有限的，一些分布的细节会在embedding中丢失
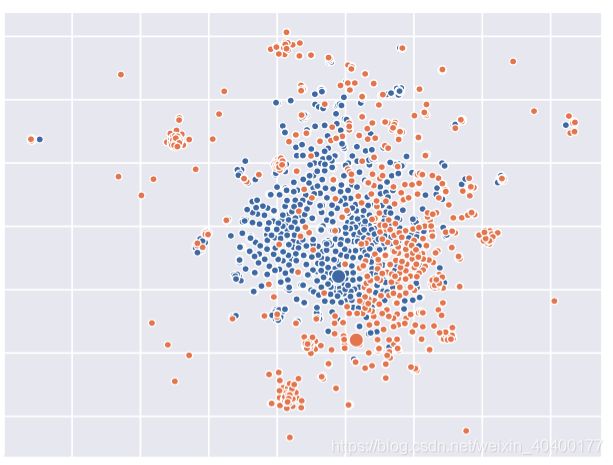
2. 直接在分布上比较会有更好的解释性。因为两个向量你无法知道具体是如何不同的，但是通过entity pairs的分布可以显然看出区别

例如在图1中，TransE的embedding会让橙色和蓝色非常接近，但是本文的模型可以捕捉两个分布之间的不同。

4. Dataset Construction

数据集构造这里不赘述，主要:

• ReVerb抽取 Wikidata(4.1, 4.2)
• FB15K
• TACRED

5. Human Judgments

作者用9位本科生去评测从Wikidata中取出的360对关系的相似度。

关系对的相似度是整数的0至4，0是无相似度，4是完全一样

本科生还有LOO来测试相关性了。（就是看他们之间给出的结果差距如何，本来就9个，确实只能用Leave one out.

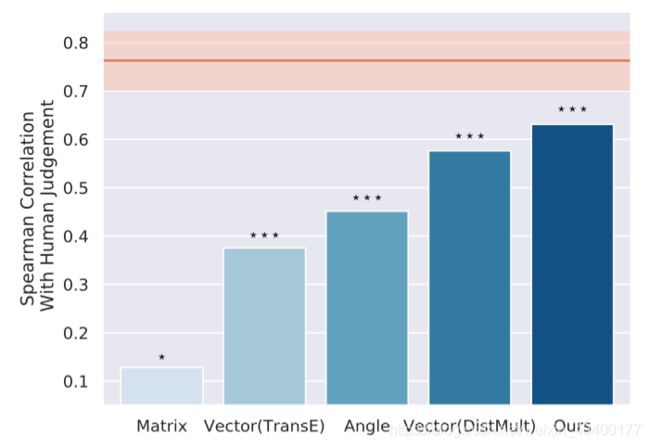
人工评测相关性是r=0.763

那么方法对比的结果为：

可以看出，模型与人工评测最为接近。相关性最高。

6. Redundant Relation Removal

OpenIE, OpenRE这里就不介绍了，这个是在是非常简单，大家可以看看我以前的博客

这里尝试用similarity度量去解决OpenIE的过度抽取问题。

6.1 Toy Experiment

设置了一个toy环境（就是用来玩玩的，和游乐场的意思差不多）

从wikidata上创建了一个数据集，并且对其使用[中国餐馆过程]，将每一个关系分为多个子关系，然后，过滤那些少于50次的，最终得到1165个关系。

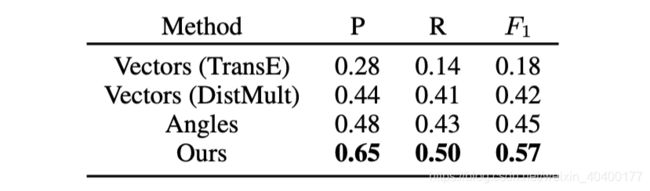
所有的这些子关系在训练过程中都被视作单独的关系

最终表格的结果显示，模型的方法，准确率和召回率都是最高的，那么F1也自然是最高的：

6.2 Real World Experiment

要来真实环境了，在训练中，每一个模式都视为单独的关系。作者采用多种关系相似度指标去合并相似的关系模式。（这可以比较不同的similarity 指标

虽然说pattern在训练的时候是label，是必须的，但是标注所有的pattern是不可能的，把所有的远程标注的结果都作为golden的结果也是不合适的（因为远程标注assumption太强了）。所以作者基于最小的人工标注，提供了一个全新的metric估计的recall和precision度量。

在标准采样中使用拒绝采样，只保留那些同义的关系对，（这一部分由人工完成）但这样效率仍然较低，因此作者使用了normalized importance sampling去获取一个对recall的无偏估计。
$$\text{Recall}=E_{x\sim U}I[\hat{f}(x)=1]\approx \sum _{i=1}^{n}I\left[\hat{f}\left(x_i\right)=1\right]{\hat{w}}_i$$

$$\text{Precision}=E_{x\sim U^{\prime }}I[f(x)=1]\approx \frac{1}{n}\sum _{i=1}^{n}I\left[f\left(x_i\right)=1\right]$$

中间部分的公式很好理解，作者对其进行了右边部分的转化，其中${\hat{w}}_i$是样本的重要性

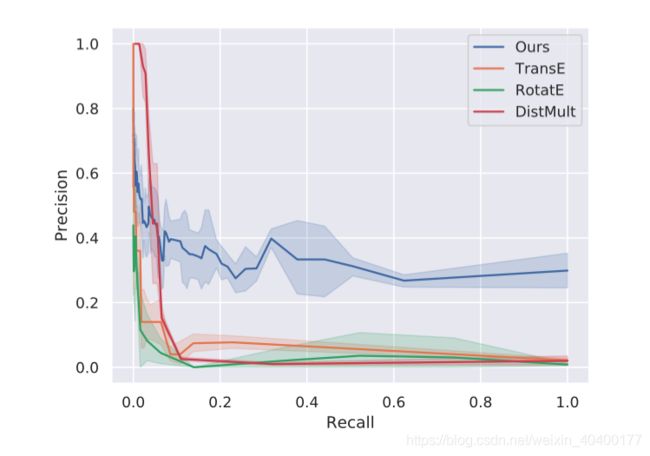
范围表示95%置信区间，relation pair是正确的，当且仅当8个人工认为他是正确且有效的。这边可以看出模型是非常之有效的。

7. Error Analysis for Relational Classification

1. relation prediction: 去预测entities之间的关系
2. relation classification: 不仅给定entities，还给定sentence

7.1 Relation Prediction

FB15K在TranE这个任务中，假设$\mathcal{D}$是训练的三元组，$d(\cdot ,\cdot )$是距离方程。 $(h^{\prime },r^{\prime },t^{\prime })$是一个负样本，并且只有一个元素与原始的$(h,r,t)$不同，这个不同的元素从三元组组合集$\mathcal{E} \times \mathcal{R} \times \mathcal{E} $标准采样。

测试过程中，对于每一个entity pair$(h,t)$， TransE 通过计算$d(h+r),t$来求出最有可能的关系。对于每一个$(h,r,t)$在测试集中，作者把TranE计算出的分数比标准答案高的关系叫做干扰关系，再去计算答案关系与干扰关系的相似度排名。

7.2 Relation Extraction

用了position-aware neural sequence model做这个任务

7.3 上述两个任务的结果见下图：

再次证明：

1. 最相似的是最具干扰的
2. 启发模型关注相似关系的边界

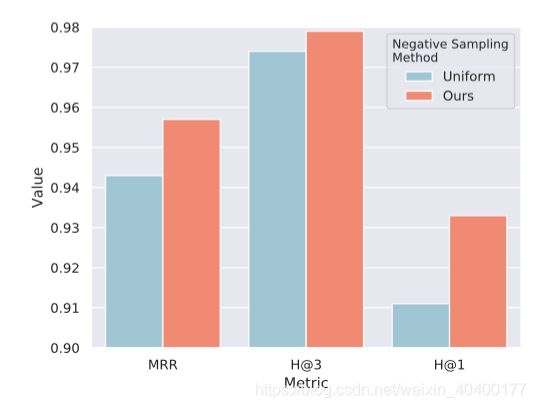
8. Similarity and Negative Sampling

根据上述结果，相似关系的三元组可以作为高质量的负样本，从而可以帮助模型学到更佳精确的决策边界。

最终结果可以如下：

9. Similarity and Softmax-Margin Loss

Softmax-Margin Loss是一个损失函数吧引入相似度，从而将relation extraction模型训练出了更好的结果。

尤其是PA-LSTM模型，具体表格见下：

总结

看完一整篇文章，感觉很累，简单的一个idea被大量的实验做出花来，非常滴不错。
自己写的顺序和逻辑应该是非常的自洽的，从头到尾看下来相信能学到不少东西。文章一共看了3小时，实在是太慢了，原本看到实验那里就不想看了，看了智源人工智能推的唐杰老师的AMiner，要专注。我就看完了[笑哭]。

另外找到一个非常不错的博主，他的解析也非常好。
地址是：
解析连接
博主连接