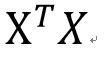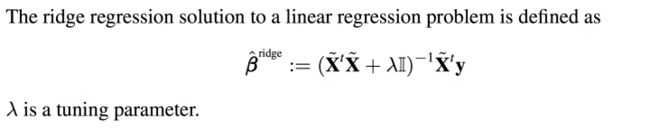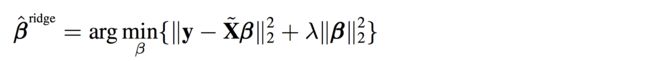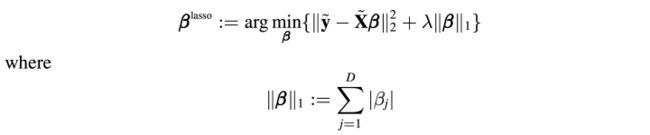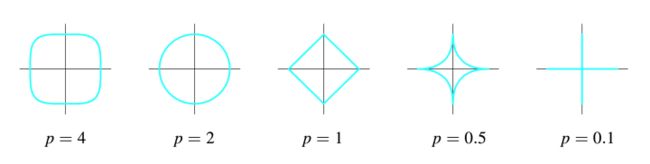我觉得这个问题首先要从“为什么普通的线性回归在很多场合不适用”开始说起,要理解这个问题一定要把大一线性代数里“空间”的概念掌握好。
首先,普通的线性回归的公式是这样的
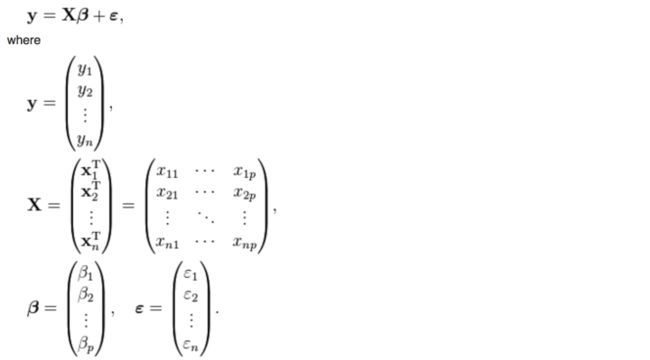
y是
被解释变量,X是
p个解释变量,我们手里有n组(y, X)的样本,然后想要通过这些样本找到一个向量beta使得

被最小化,满足这个最小化条件的beta就是线性回归要寻找的beta,数学上可以证明这个问题是有通解的:

也就是说,只有我们手里有X和Y这两个矩阵(向量),把它们带入上面的公式就能得到我们想要的beta,然后就能用beta和新的Xi来对未知的Yi进行预测了。
然而,上面这个公式有一个问题,
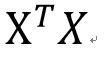
这两个矩阵相乘的结果,一个p*p的矩阵(p是解释变量的个数),一定是可逆的吗?不可逆的话刚才算beta的公式不就没有意义了吗?
幸运的是,在实际生活中,只要我们的数据真的是随机抽取的,这个矩阵一般都是可逆的。
不幸的是,有一种存在叫做
almost singular。
一个方阵(行数=列数, 比如上面那个p*p矩阵)一定可以被归类到以下两种情况:
singular: 行列式|X|=0,特征根中至少有一个是0,不满秩,不可以求逆。
nonsingular: 行列式|X|不等于0,特征根都不等于0,满秩,可以求逆。
这个矩阵
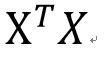
肯定是nonsingular的可以求逆,但是在一些情况下(比如multicollinearity),这个矩阵的行列式的值可能非常非常非常小(比如0.000000001),于是X只要有一个微小的变化,它的逆矩阵就会有一个很大很大的变化,导致你用不同的样本估计出来的beta的差别非常非常大,这样的矩阵就叫almost singular。
almost singular: 行列式|X|几乎等于0,特征根有一个或多个接近于0,满秩,可以求逆,但是
对X进行微小的改变会导致
逆矩阵发生巨大的改变。
大家想一想,如果你用1点钟收集到的数据估出来的参数等于100,3点钟收集到的数据估出来的参数等于100000,那你到底要用哪一个?到底哪一个是对的?你并不知道。
这个问题就是楼上有人提出的“estimator 的数值解可能不存在/极不稳定”的情况。
那么如何解决呢?当然要对症下药啦。既然这个矩阵的行列式近似等于0,那我在它的对角线上全部加上一个常数不就行了嘛?
于是ridge regression就被发明出来了:
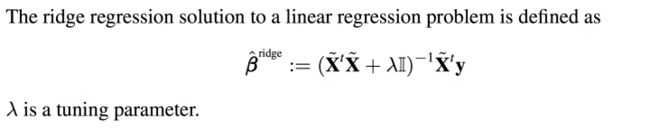
其实就是在刚刚Beta的解的公式的基础上进行了微小的调整,I是单位矩阵,lamda是通过cross validation来确定的,并不是需要估计的参数。这个调整就是楼上有人说的regularization。
你可能会很疑惑,如果说线性回归是在最小化下面这个方程:

那ridge regression是在最小化什么东西呢?数学上也可以证明,上面新的beta的解,其实就是在最小化下面这个式子:
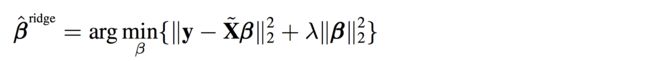
其实就是在上面的式子后面多加了一项而已。
你可能又要问了,多加的那一项凭什么是模长呢?不能把2-norm改成1-norm吗?
答案是可以的,
这种情况就是lasso了:
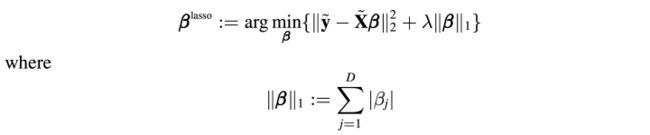
遗憾的是,lasso是不能像ridge regression和linear regression一样写出“显式解”的,必须用数值方法去近似上面的优化问题的解。
幸运的是,统计学家发现用lasso算出来的beta的很多项是0,也就是说你在估计参数的时候顺带着把model selection也一起做了,
买一送一哦亲!
为什么会这样呢?上面有答主传了一副图:
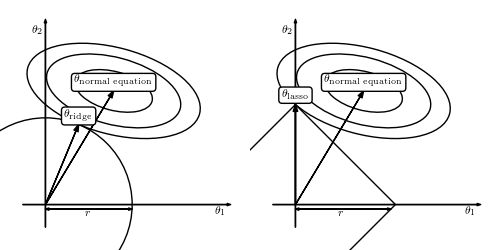
因为lasso选了1-norm,导致theta-lasso的范围“有棱有角”,在和normal equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话,就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。
简而言之,
不想做数值优化,想要一个确定的解,选ridge regression吧!
不想做完参数估计还要做model selection挑选变量,选lasso吧!
可是新的问题又出现了,ridge regression选了2-norm,lasso选了1-norm,那我能不能把这个问题拓展到p-norm的情形呢?(这个p和刚才的解释变量的个数p是两个概念)
答案是可以的,只要p大于等于1就行了。
p为什么不能小于1?因为p小于1时刚才那幅图里的圆形和正方形会继续“往里陷”,变成下面的样子:
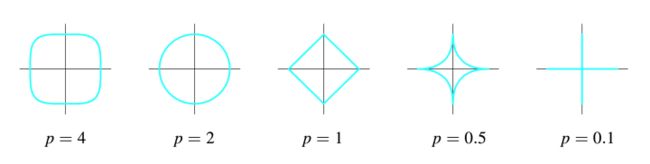
这样这个集合就不是convex set了,没有办法做最优化了,which is another long story。
最后回到一开始“空间”的问题,为什么我说理解这个问题“空间”的概念非常重要呢?
其实线性回归的本质,是把一个n维空间的向量Y投射到p+1维空间,这个p+1维空间就是p个X解释变量和一个常数向量,这p+1个向量span出来的一个“亚空间”。因为Y本身在n维空间太复杂了,而我们生活在p+1维空间(一般情况下p+1远小于n),我们能做的就是把Y投射到我们所在的p+1维空间,
尽可能的去获得更多的Y的信息。然而,有些时候因为X数据本身出现了一些问题,p+1维空间发生了“退化”或者“坍塌”,为了“支撑”起这个空间,我们在对角线上都加了一个常数,撑起了一个新的空间,这就是regularization的基本思路。
你可能又要问了,有没有可能不用投射到p+1维空间,我们直接在n维空间找到Y的全部信息呢?
答案是可以的,但是这就不叫线性回归了,这叫
解线性方程组(p+1=n)。
所以说,线性代数真的很重要啊。