匈牙利算法,寻找最大匹配
讲述匈牙利算法如何寻找二分图的最大匹配,本文分为3个部分:
1. 二分图的基本知识点
2. 匈牙利树
3. 具体例子
1. 二分图的基本知识点
原地址:https://www.cnblogs.com/wangjunyan/p/5563154.html
其中蓝色字体为自己添加的部分
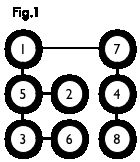
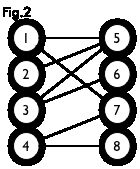
二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交集 UU 和VV ,使得每一条边都分别连接UU、VV中的顶点。如果存在这样的划分,则此图为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰,我们以后都把它画成图 2 的形式。
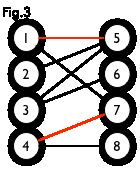
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
举例来说:如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?图论中,这就是完美匹配问题。如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?这就是最大匹配问题。
基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法,下面讲的概念都为这个算法服务。
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
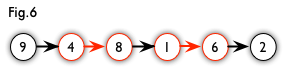
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):(Augument Path: 第一个点和最后一个点都是未匹配点)
增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了 1 条。(颠倒之后就会变成cardinality+1,所以这就是Berge所说的当找不到Augument Path时就是最大匹配)
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前,先讲一下匈牙利树。
2. 匈牙利树
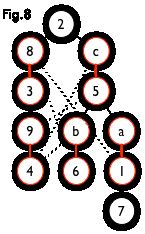
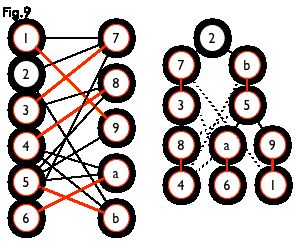
匈牙利树一般由 BFS 构造(类似于 BFS 树)。从一个未匹配点出发运行 BFS(唯一的限制是,必须走交替路)交替路就是匈牙利树与普通的广度优先算法得出的BFS的不同,直到不能再扩展为止。二分图的最大匹配可以通过匈牙利树的搜索寻找增广路径来获得例如,由图 7,可以得到如图 8 的一棵 BFS 树:
这棵树存在一个叶子节点为非匹配点(7 号),但是匈牙利树要求所有叶子节点均为匹配点(重点),因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点,那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示(顺便说一句,图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路,沿这条增广路扩充后将得到一个完美匹配)。
匈牙利树就是存在的可连接的匹配点都列出来(BFS)
最后再看一下由增广路径的定义可以推出的三个结论:
①P的路径长度必定为奇数,第一条边和最后一条边都不属于M
②P经过取反操作可以得到一个更大的匹配M
③M为G的最大匹配当且仅当不存在相对于M的增广路径
3. 具体例子(本处是我自己制作的一个例子,此处不贴代码,代码可以到原地址去找)
步骤1.一开始为空匹配,此时我选择匹配1-a
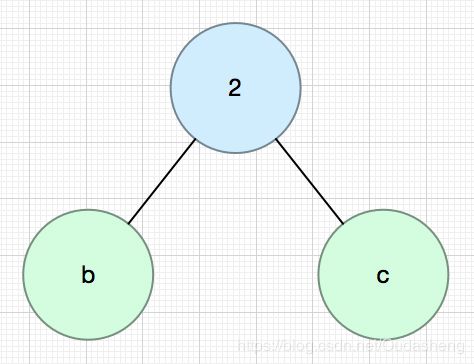
步骤2.根据图b建立类BFS树,可选择的空匹配点为2, 3, 4, a, b, c
由空匹配点2建立的类BFS树(有增广路径),所以建立增广路径2-b(你也可以2-c)
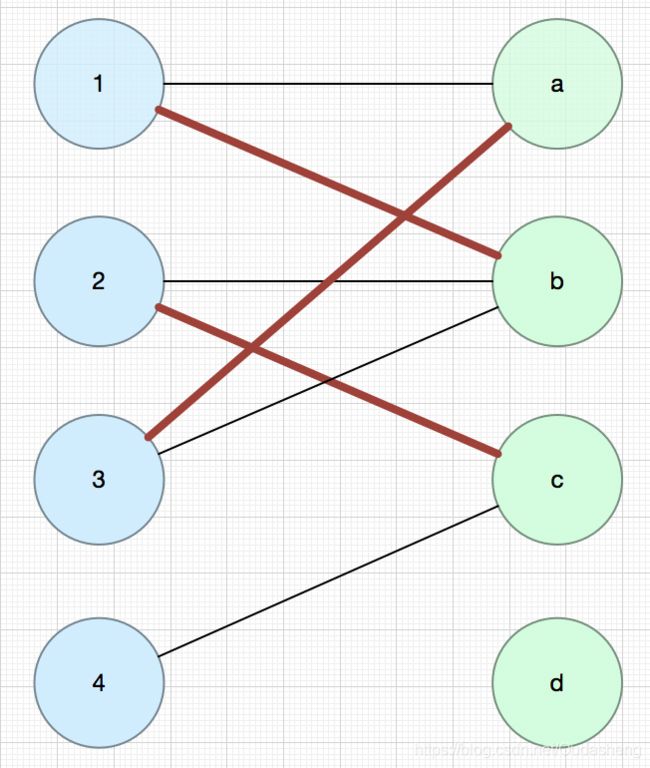
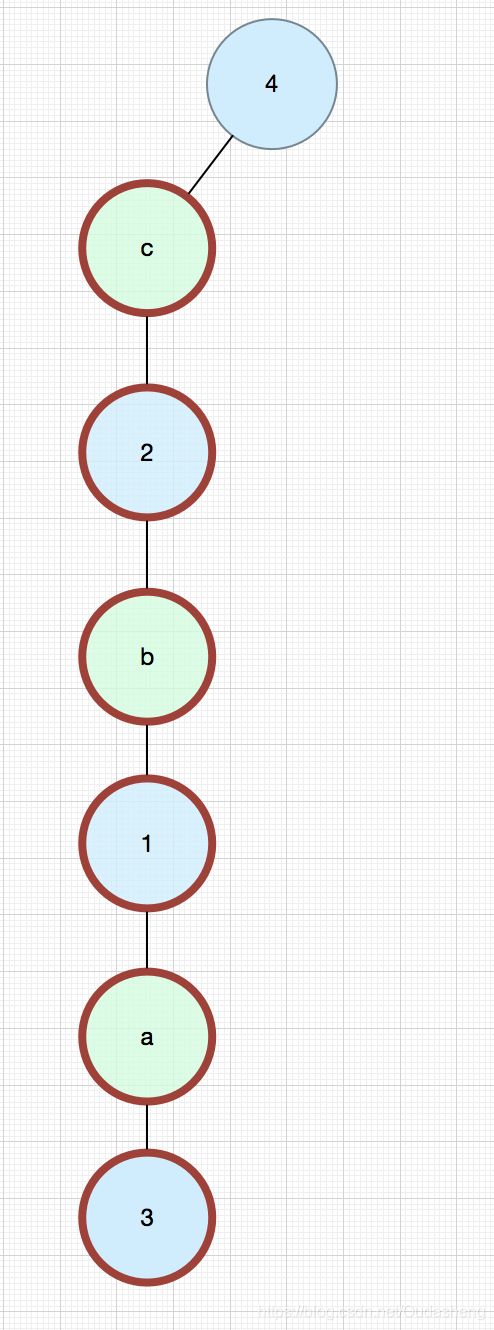
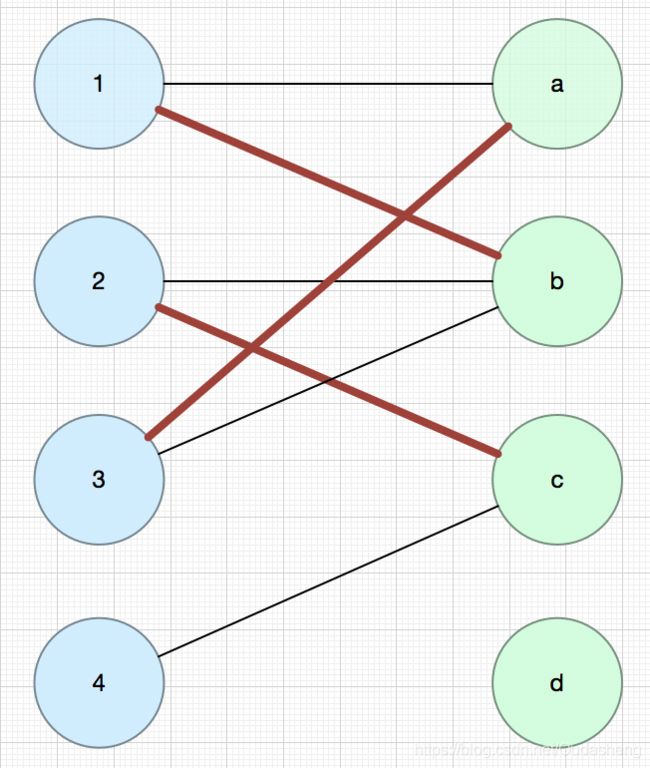
根据上面右图建立关于空匹配点3的类BFS树(有增广路径),所以建立路径3-a-1-b-2-c
建立空匹配点4的匈牙利树,无增广路径,因为所有的叶结点都是匹配点。
步骤3.最后的最大匹配结果为: