机器学习(吴恩达)-6 神经网络的基础知识
本文是博主最近的机器学习笔记,如果有不正确的地方还请指正,谢谢~
目录
- 铺垫——需要神经网络的原因
- 神经网络模型展示
- 神经网络的简单应用
铺垫——需要神经网络的原因
神经网络也是用来解决监督问题的机器学习算法,而目前针对监督问题我们已有线性回归和逻辑回归这两种学习算法了,为何还需要神经网络来处理呢? 我们来通过一个例子说明:
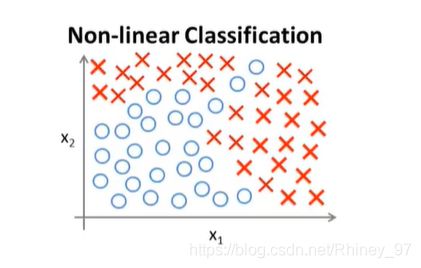
上图是一个非线性回归的分类问题,对数据点的类别根据 x 1 , x 2 x_1,x_2 x1,x2两个特征来确定。针对分类问题,我们可以使用已学过的逻辑回归方法来研究,假设函数为以下形式:
h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 x 2 + θ 4 x 1 2 x 2 . . . ) h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1x_2+\theta_4x_1^2x_2...) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x1x2+θ4x12x2...)
当特征只有两个时,假设函数中的 g ( z ) g(z) g(z)内特征项并不多,完全能够计算出来,得出的假设曲线也可以较好的拟合数据的分类。
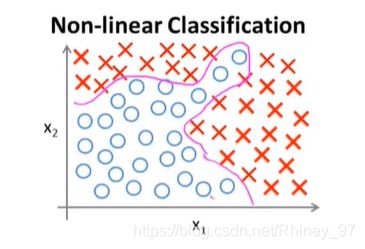
但是如果某个分类问题中特征项较多,如有100项( x 1 , x 2 x 3 , . . . x 100 x_1,x_2x_3,...x_{100} x1,x2x3,...x100),那么需要计算的假设函数中的 g ( z ) g(z) g(z)中就有可能包含有成百上千的特征项了,如此多的特征项一方面带来的计算量会变大大,另一方面也可能会造成过拟合的情况(且针对过拟合使用正则化可能并不是那么有效)。
另外再给一个例子:
计算机视觉也是机器学习的一个应用,计算机视觉主要是通过给计算机一个图片,让它分辨图片中是否有某物体。
拿汽车的图片来说,计算机视觉通过已知的一系列“是汽车”图片和“不是汽车”图片,来分辨出给出的一个图片是否是汽车图片。

具体是如何进行判断?拿上图的汽车图片中的门把手来说,图中门把手部分存储在计算机中就是图中右下角的颜色灰度矩阵,矩阵中是每个像素点的灰度值,而这个灰度值矩阵代表了这是一个门把手。
计算机将灰度值矩阵中的每个灰度值作为一个特征,假如门把手的图片分辨率是50*50,那么图片一共有2500个像素点,特征数n=2500。 通过计算机中已存储的门把手和非门把手,可以得到一个特征数为2500的分类问题。计算机的目的就是通过学习已给出的训练集,来判断下一个图片是否是门把手。
具体简化一下,我们假设对于一个汽车图片,只采取其中的两个像素点 x 1 , x 2 x_1,x_2 x1,x2来判断这个图片中是否是汽车(当然很不现实,主要举例用):
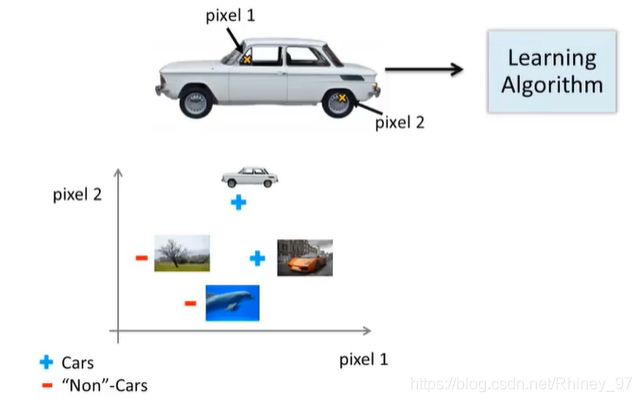
图中右下角已给出了四个数据点,横纵坐标分别为这两个像素点的灰度值,坐标中有两个是汽车,两个不是汽车,那么再增加更多的图片:
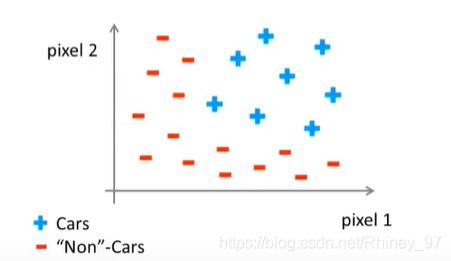
从上图可以看出这是一个分类问题,理论上来说可以使用逻辑回归来解决。
但是实际上不行,因为首先分辨一个图像中的物体不是可以仅靠两个像素点就能完成的。 在上面的门把手例子中,我们假设了门把手部分的图片大小为50*50,也就是2500个像素点,需要2500个特征数( x 1 , x 2 , x 3 , . . . , x 2500 x_1,x_2,x_3,...,x_{2500} x1,x2,x3,...,x2500),而这些特征在逻辑回归中的假设函数 g ( z ) g(z) g(z)内,会需要多个特征相乘作为一项,从而扩展出更多的特征项,就算不考虑可能的平方项,只考虑两两特征相乘作为一项:
h θ ( x ) = g ( θ 12 x 1 x 2 , θ 13 x 1 x 3 , θ 14 x 1 x 4 , . . . . . . , θ 23 x 2 x 3 , θ 24 x 2 x 4 , . . . . . . ) h_\theta(x)=g(\theta_{12}x_1x_2,\theta_{13}x_1x_3,\theta_{14}x_1x_4,......,\theta_{23}x_2x_3,\theta_{24}x_2x_4,......) hθ(x)=g(θ12x1x2,θ13x1x3,θ14x1x4,......,θ23x2x3,θ24x2x4,......)
也会有上百万个参数项,计算量非常的大,在这种情况下,目前的逻辑回归算法只会无力承担如此庞大的计算量。因此在特征数量达到一个较大值时,我们需要一个更加有效的机器学习算法来处理此类问题。
这也是需要神经网络学习算法的原因。神经网络可以在n(特征数)很大时仍有效地解决这些复杂的非线性假设问题。
神经网络模型展示
神经网络顾名思义,模仿的是人大脑中的神经元组成的网络。神经元包括细胞体和突起两部分:细胞体是神经元的本体,用来处理整合接收到的信息;突起包括轴突和树突,用来接收外来信号并传送信号给其他神经元。
根据神经元模仿的神经网络算法中,单个的逻辑单元如下所示:
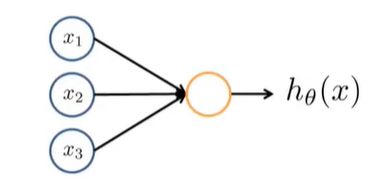
其中 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3为表示输入的特征,中间的橘色圆圈表示处理单元,最后输出到 h θ ( x ) h_\theta(x) hθ(x)中,得到结果。
上图是最简化的逻辑单元,将这个逻辑单元再扩展一下:
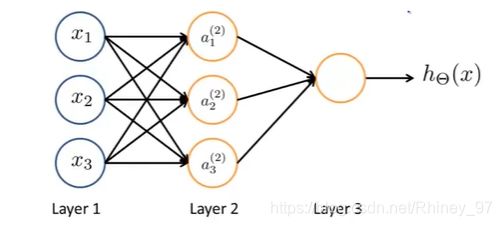
中间多了一层,Layer 1(第一层)也称作输入层,Layer 2(第二层)也称作隐藏层,Layer 3(第三层)也称作输出层,有时也不仅仅包括这三个层,但是不管有多少层,输入层和输出层均只有一个,其他的都是中间的隐藏层。
输入层中的 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3很好理解,就是相当于逻辑回归中的特征项,将每个特征项的值输入以后进行处理。输出层也很好理解,即得到的假设函数的值,也可以认为是通过中间的算法处理后得到的判断结果。
中间的隐藏层含有 a 1 ( 2 ) , a 2 ( 2 ) , a 3 ( 2 ) a_1^{(2)},a_2^{(2)},a_3^{(2)} a1(2),a2(2),a3(2),共有三项,其中的上标“ ( 2 ) ^{(2)} (2)”表示这是第二层的项,即第二层中含有 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3三项。 a i a_i ai表示这是一个激活项(激活项的意思是由一个具体神经元计算并输出的值。就像一个函数一样,输入具体的参数值,就可以计算并返回出一个结果值)。
有时为了参数对应的一致,会加上 x 0 x_0 x0, a 0 a_0 a0,原理与学习逻辑回归算法一样。
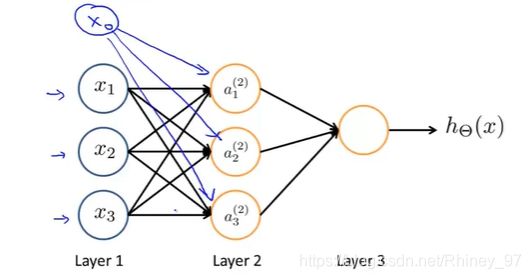
隐藏层的激活项和输出层具体内容如下:
a 1 ( 2 ) = g ( θ 10 ( 1 ) x 0 + θ 11 ( 1 ) x 1 + θ 12 ( 1 ) x 2 + θ 13 ( 1 ) x 3 ) a_1^{(2)}=g(\theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1+\theta_{12}^{(1)}x_2+\theta_{13}^{(1)}x_3) a1(2)=g(θ10(1)x0+θ11(1)x1+θ12(1)x2+θ13(1)x3)
a 2 ( 2 ) = g ( θ 20 ( 1 ) x 0 + θ 21 ( 1 ) x 1 + θ 22 ( 1 ) x 2 + θ 23 ( 1 ) x 3 ) a_2^{(2)}=g(\theta_{20}^{(1)}x_0+\theta_{21}^{(1)}x_1+\theta_{22}^{(1)}x_2+\theta_{23}^{(1)}x_3) a2(2)=g(θ20(1)x0+θ21(1)x1+θ22(1)x2+θ23(1)x3)
a 3 ( 2 ) = g ( θ 30 ( 1 ) x 0 + θ 31 ( 1 ) x 1 + θ 32 ( 1 ) x 2 + θ 33 ( 1 ) x 3 ) a_3^{(2)}=g(\theta_{30}^{(1)}x_0+\theta_{31}^{(1)}x_1+\theta_{32}^{(1)}x_2+\theta_{33}^{(1)}x_3) a3(2)=g(θ30(1)x0+θ31(1)x1+θ32(1)x2+θ33(1)x3)
h θ ( x ) = a 1 ( 3 ) = g ( θ 10 ( 2 ) a 0 ( 2 ) + θ 11 ( 2 ) a 1 ( 2 ) + θ 12 ( 2 ) a 2 ( 2 ) + θ 13 ( 2 ) a 3 ( 2 ) ) h_\theta(x)=a_1^{(3)}=g(\theta_{10}^{(2)}a_0^{(2)}+\theta_{11}^{(2)}a_1^{(2)}+\theta_{12}^{(2)}a_2^{(2)}+\theta_{13}^{(2)}a_3^{(2)}) hθ(x)=a1(3)=g(θ10(2)a0(2)+θ11(2)a1(2)+θ12(2)a2(2)+θ13(2)a3(2))
分析一下激活项 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3的等式内容,可以发现后面的等式是逻辑回归中假设函数的等式: h θ ( x ) = g ( z ) h_\theta(x)=g(z) hθ(x)=g(z)。因此,每个激活项中都是与逻辑回归中相似的计算方法,激活项之间不同的不是公式,而是输入的特征值。
而输出层就是将 a 1 ( 2 ) , a 2 ( 2 ) , a 3 ( 2 ) a_1^{(2)},a_2^{(2)},a_3^{(2)} a1(2),a2(2),a3(2)作为输入的特征进行计算并得出结果。其中 a 1 ( 3 ) a_1^{(3)} a1(3)仅表示这是第三层的第一个激活项。
如果将隐藏层的激活项中内容作以下赋值:
z 1 ( 2 ) = θ 10 ( 1 ) x 0 + θ 11 ( 1 ) x 1 + θ 12 ( 1 ) x 2 + θ 13 ( 1 ) x 3 z_1^{(2)}=\theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1+\theta_{12}^{(1)}x_2+\theta_{13}^{(1)}x_3 z1(2)=θ10(1)x0+θ11(1)x1+θ12(1)x2+θ13(1)x3
z 2 ( 2 ) = θ 20 ( 1 ) x 0 + θ 21 ( 1 ) x 1 + θ 22 ( 1 ) x 2 + θ 23 ( 1 ) x 3 z_2^{(2)}=\theta_{20}^{(1)}x_0+\theta_{21}^{(1)}x_1+\theta_{22}^{(1)}x_2+\theta_{23}^{(1)}x_3 z2(2)=θ20(1)x0+θ21(1)x1+θ22(1)x2+θ23(1)x3
z 3 ( 2 ) = θ 30 ( 1 ) x 0 + θ 31 ( 1 ) x 1 + θ 32 ( 1 ) x 2 + θ 33 ( 1 ) x 3 z_3^{(2)}=\theta_{30}^{(1)}x_0+\theta_{31}^{(1)}x_1+\theta_{32}^{(1)}x_2+\theta_{33}^{(1)}x_3 z3(2)=θ30(1)x0+θ31(1)x1+θ32(1)x2+θ33(1)x3
那么:
z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] z^{(2)}=\begin{bmatrix} z_1^{(2)} \\ z_2^{(2)} \\ z_3^{(2)} \end{bmatrix} z(2)=⎣⎢⎡z1(2)z2(2)z3(2)⎦⎥⎤
设:
x = [ x 0 x 1 x 2 x 3 ] , θ ( 1 ) = [ θ 10 θ 11 θ 12 θ 13 θ 20 θ 21 θ 22 θ 23 θ 30 θ 31 θ 32 θ 33 θ 40 θ 41 θ 42 θ 43 ] x=\begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3 \end{bmatrix} ,\theta^{(1)}= \begin{bmatrix} \theta_{10}& \theta_{11}&\theta_{12}&\theta_{13}\\ \theta_{20}& \theta_{21}&\theta_{22}&\theta_{23}\\ \theta_{30}& \theta_{31}&\theta_{32}&\theta_{33}\\ \theta_{40}& \theta_{41}&\theta_{42}&\theta_{43} \end{bmatrix} x=⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤,θ(1)=⎣⎢⎢⎡θ10θ20θ30θ40θ11θ21θ31θ41θ12θ22θ32θ42θ13θ23θ33θ43⎦⎥⎥⎤
则可得:
a ( 2 ) = g ( z ( 2 ) ) a^{(2)}=g(z^{(2)}) a(2)=g(z(2))
同理可以得到输出层的公式:
z ( 3 ) = θ ( 2 ) a ( 2 ) z^{(3)}=\theta^{(2)}a^{(2)} z(3)=θ(2)a(2) h θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) h_\theta(x)=a^{(3)}=g(z^{(3)}) hθ(x)=a(3)=g(z(3))
神经网络的简单应用
通过一个非常简单的例子,我们来了解一下神经网络是如何实际应用的。
现希望通过非线性分类来推测两特征 x 1 , x 2 x_1,x_2 x1,x2异或的结果,下图给出了许多训练样本,最终目的是希望能够学习一个非线性的判断边界:
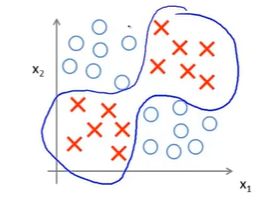
在这里为了将问题简化,更好分析,我们可以把 x 1 , x 2 x_1,x_2 x1,x2简化为二进制,只能取值0或1,只用下面四个训练样本:
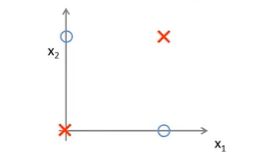
y = x 1 X O R x 2 y=x_1\,\, XOR\,\,x_2 y=x1XORx2(y为异或得到的结果),上图中两个圆圈为结果 y = 0 y=0 y=0,红叉为 y = 1 y=1 y=1 。
为了能够解决这个问题,通过以下三个小例子来铺垫:
①有 x 1 , x 2 ∈ { 0 , 1 } x_1,x_2\in\{0,1\} x1,x2∈{0,1}, y = x 1 A N D x 2 y=x_1\,AND\,x_2 y=x1ANDx2,即学习推测两特征与的结果。
我们增加一个特征 x 0 x_0 x0,将 x 0 , x 1 , x 2 x_0,x_1,x_2 x0,x1,x2分别赋值为-30,20,20:
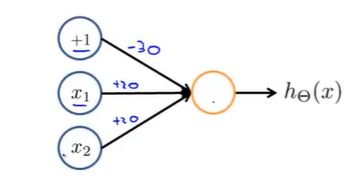
得到的假设函数:
h θ ( x ) = g ( − 30 + 20 x 1 + 20 x 2 ) h_\theta(x)=g(-30+20x_1+20x_2) hθ(x)=g(−30+20x1+20x2)
从而通过表格分析做出的假设函数是否符合要求:
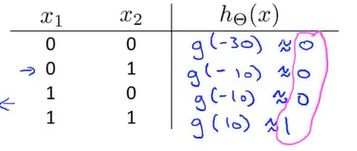
通过粉色笔记画出的估算值可以看出这个假设函数是符合题目要求的,计算出的值与 x 1 x_1 x1和 x 2 x_2 x2相与的结果一致。
②通过寻找合适的假设函数,实现其推测结果与 x 1 O R x 2 x_1\,OR \,x_2 x1ORx2(或运算)一致:
设 x 0 x_0 x0=-10, x 1 x_1 x1=20, x 2 x_2 x2=20,得到 h θ ( x ) = g ( − 10 + 20 x 1 + 20 x 2 ) h_\theta(x)=g(-10+20x_1+20x_2) hθ(x)=g(−10+20x1+20x2),最终计算结果符合要求。

③寻找合适的假设函数,实现 N O T x 1 NOT\,x_1 NOTx1(非运算):
设 x 0 x_0 x0=10, x 1 x_1 x1=-20,得到 h θ ( x ) = g ( 10 − 20 x 1 ) h_\theta(x)=g(10-20x_1) hθ(x)=g(10−20x1),最终计算结果符合要求。
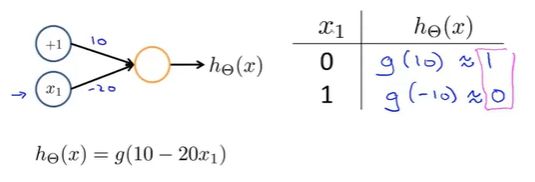
现在回归到最开始的例子中,为了通过假设函数的计算得到近似异或运算的结果,我们需要将上面形式的小例子结合起来:
把" x 1 A N D x 2 x_1\,AND\,x_2 x1ANDx2“的结果作为中间值(激活项) a 1 ( 2 ) a_1^{(2)} a1(2),” ( N O T x 1 ) A N D ( N O T x 2 ) (NOT\,x_1)\,AND\,(NOT\,x_2) (NOTx1)AND(NOTx2)"的结果作为中间值(激活项) a 2 ( 2 ) a_2^{(2)} a2(2),最后令 a 2 ( 2 ) a_2^{(2)} a2(2)=-10,得到如下的过程:
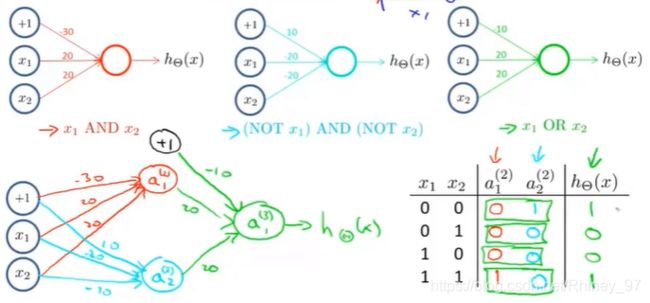
上图中左下角是最终的神经网络分布形式,右下角便是最终计算得到的结果,其结果与 x 1 x_1 x1异或 x 2 x_2 x2的结果一致,因此是符合题意的。
从以上的例子中可以看到计算过程中使用到的参数很少,并且结果是分层计算出来的,因此可以有效地解决特征量过多的问题。