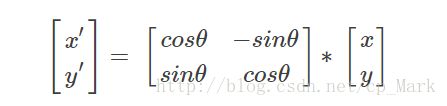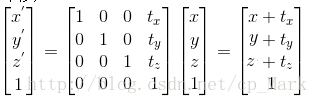OpenGL ES系列一--向量和矩阵

OpenGL ES之向量、矩阵

OpenGL ES是一个很强大的库，可以绘制各种酷炫的3D图形，既然涉及到3D图形，那么跟3D数学肯定是脱离不了关系的，在我们正式进行OpenGL ES之前，我们需要先搞清楚一些数学上的东西，这样在你后面进一步学习OpenGL ES的时候才不至于懵逼。主要涉及到的一些数学概念有：

1. 向量
   
   • 向量的定义
   • 向量的加法、减法
   • 向量的乘法（数乘、点乘、叉乘）
2. 矩阵
   
   • 矩阵的定义
   • 矩阵的乘法（数乘、乘法、向量和矩阵的乘法）
   • 一些常见的矩阵变换：缩放、投影、平移等（含4维齐次坐标的使用）

向量

向量的定义

定义：数学上区分向量（矢量）和标量（数量），标量就是我们平常所用的数字，强调数量值；向量的话其实就是带有方向的标量，常用有向线段表示。向量根据所在的坐标系（平面坐标、3D坐标、4D坐标等），分为2维坐标、3维坐标等，依次类推

向量的大小就是向量的长度（模），长度非负。计算方式为向量各分量的平方之和开平方，比如二维向量

​ 向量的方向描述了空间中向量的指向。箭头是向量的末端（向量“结束”于此），箭尾是向量的“开始”

日常生活中很多量都有大小和方向，比如：位移（向前三步，由大小三步和方向向前构成）、速度（我们以50公里每小时的速度向北行驶，由大小50公里每小时和方向北构成），注意位移和速度与距离、速率是完全不同的，前两者为向量，后两者为标量。

一些常用的向量类型：

类型名	定义
法向量	垂直于平面的直线所表示的向量为该平面的法向量。由于空间内有无数个直线垂直于已知平面，因此一个平面都存在无数个法向量
标准化向量（法线）	向量大小为1的向量称为单位向量，单位向量经常也被称作标准化向量或更简单地秤为法线。对于任意非零向量v，都能计算出一个和v方向相同的单位向量，这个过程被称作向量的“标准化”，要标准化向量，将向量除以它的大小（模）即可。（零向量不能标准化）

OpenGL ES在求光照的时候会用到法向量和标准化向量，具体的我们在涉及到光照的知识的地方会说明。

向量的加法和减法

向量加法的运算法则：两个向量相加，将对应的分量相加即可（前提条件：两个向量的维数相同）。

设a=(x1,y1)，b=(x2,y2)，则a+b=(x1+x2,y1+y2)

向量减法的运算法则：向量减法解释为加负向量（条件同上）

a=(x1,y1)，b=(x2,y2) ，则a-b=(x1-x2,y1-y2).

注意：

1. 向量不能与标量或者维数不同的向量相加减
2. 向量加法满足交换律，但是向量减法不满足交换律

补充知识点：在OpenGL ES中，颜色、纹理、光照等都是使用向量来表示的，以颜色为例：

//这是一段GLSL着色器程序，其很多语法和c++相似。vec4表示4维向量
//在此处vec4的4个分量分别是r、g、b、a
vec4 colorA;
vec4 colorB;
void main(){
    //这是GLSL的内置函数，为片元设置颜色，这里就使用到了向量相加（各对应的分量相加）
    gl_FragColor = colorA +colorB;
}

向量的乘法

数乘（标量和向量的乘法）

标量和向量不能相加，但它们能相乘，将得到一个与原向量平行，但长度不同或方向相反的向量。

标量与向量的乘法满足交互律，将向量的每个分量都与标量相乘即可。向量也能除以非零标量，效果等同于乘以标量的倒数

注意：标量不能除以向量，并且向量不能除以另一个向量

向量点乘

向量点乘，也称内积，是对应分量乘积的和，结果是一个标量，其结果也等于向量大小与向量夹角的cos值的积，示例如下。满足交换律

设向量:

a(x1, y1, z1) b(x2,y2,z2)

所以点乘结果为：

a · b = |a||b|cos<a, b>

a · b = x1*x2 + y1*y2 + z1*z2

意义：一般来说，点乘结果描述了两个向量的相似程度，结果越大，两向量越相近。

向量叉乘

向量叉乘，也称叉积，仅可应用于3D向量，结果是一个垂直于原来两个向量的向量，可以理解为法向量。需要注意的是不满足交换律

叉乘的长度等于向量的大小与向量夹角的sin值的积

设向量:

a(x1, y1, z1) b(x2,y2,z2)

叉乘结果为向量：

a X b = (y1*z2 – z1*y2, z1*x2 – x1*z2, x1*y2 – y1*x2)

叉乘结果的长度：

∣a**X**b∣=|a|·|b|·sin〈a，b〉，sin〈a，b〉为向量a、b的夹角

矩阵

矩阵的定义

定义：矩阵是3D数学的重要基础，常用来描述两个坐标系统间的关系，通过定义一种运算而将一个坐标系中的向量转换到另一个坐标系中

矩阵类型	说明
方阵	行数和列数相同的矩阵称作方阵，方阵的对角线元素就是方阵中行号和列号相同的元素，其他均为非对角线元素。
单位矩阵	非对角线元素都为0，对角线元素全为1的特殊方阵为单位矩阵。单位矩阵是矩阵的乘法单位元，任意一个矩阵乘以单位矩阵，得到的还是原矩阵
向量	向量可以理解为特殊的矩阵，怎么特殊呢？如果矩阵的行数，或者列数为1，那么矩阵就成了向量，1xn矩阵称作行向量，nx1矩阵称作列向量

矩阵乘法

矩阵乘法包含数乘、乘法、向量乘矩阵，具体如下：

数乘

当标量乘以矩阵时，以标量乘以矩阵中的各分量，示例如下图：

乘法

矩阵能够相乘的前提条件：设当前有两个矩阵A、B，矩阵A的列数要和矩阵B的行数相同，其结果为一个A的行数，B的列数的矩阵AB。

rxn矩阵A与nxc矩阵B的积 rxc矩阵AB为C，C中的任意元素等于A的对应行向量与B的对应列向量的点乘结果。示例如下：

注意：

1. 矩阵乘法不满足交换律
2. 矩阵乘法满足结合律
3. 矩阵乘法满足与标量或向量的结合律

在OpenGL ES中我们经常将多个变换矩阵先乘，结合成一个总变换矩阵再传给着色器使用

向量和矩阵的乘法（向量其实是特殊矩阵，所以只有满足矩阵乘法的向量*矩阵才有意义）

行向量左乘矩阵时，结果是行向量；右乘无意义；列向量右乘矩阵时，结果是列向量；左乘无意义。以下为列向量右乘矩阵的示例：

由上面的示例可以看出，当原列向量右乘矩阵之后，原列向量的x、y、z发生变化，都乘以一个系数，可以理解为向量乘以矩阵之后所得到的新向量经过矩阵的线性变换的

一些常见的矩阵变换：缩放、投影、平移等（含4维齐次坐标的使用）

缩放

在各个方向应用同比例的缩放，并且沿着原点“膨胀”物体，那么就是均匀缩放，均匀缩放可以保持物体的角度和比例不变。如果长度增加或减少因子k，则2D增加或减小因子k的平方，在3D中，体积的因子是k的立方，一次类推。

如果需要挤压或拉伸物体，在不同的方向应用不同的因子即可，这称作非均匀缩放。如果|k|<1,物体将变短；如果|k|>1,物体边长；如果|k|=0，就是正交投影；如果k<0，就是镜像。

图中显示，x、y、z分别乘以三个缩放因子，起到缩放的作者用

旋转

首先要明确旋转在二维中是绕着某一个点进行旋转，三维中是绕着某一个轴进行旋转。我们这里以2维为例，如下图所示：

如图所示点v 绕 原点旋转θ 角，得到点v’，假设 v点的坐标是(x, y) ，那么可以推导得到 v’点的坐标（x’, y’)(设原点到v的距离是r，原点到v点的向量与x轴的夹角是ϕ )

//x、y值
x=rcosϕ
y=rsinϕ 

//旋转过后的x、y值
x′=rcos(θ+ϕ)
y′=rsin(θ+ϕ) 

//通过三角函数展开旋转结果
x′=rcosθcosϕ−rsinθsinϕ 
y′=rsinθcosϕ+rcosθsinϕ 

//带入x、y，得到最终结果
x′=xcosθ−ysinθ 
y′=xsinθ+ycosθ 

写成矩阵的形式是：

平移

在计算机图形学中，为了统一将平移、旋转、缩放等用矩阵表示，需要引入齐次坐标。（假设使用2x2的矩阵，是没有办法描述平移操作的，只有引入3x3矩阵形式，才能统一描述二维中的平移、旋转、缩放操作。同理必须使用4x4的矩阵才能统一描述三维的变换）。我们这里以三维变换为例，如下图为平移的一种矩阵形式：

变换的组合

变换是由矩阵来实现的，所以变换的组合实际上就是矩阵的组合，从代数角度来看是利用了矩阵乘法的结合律。我们以二维旋转为例（旋转点是不过原点的，所以此旋转是旋转和平移的组合），二维旋转以点为旋转中心，此时我们需要执行以下步骤：

1. 将旋转点一到原点
2. 绕原点旋转
3. 再将旋转点移回原来的位置

从上面可以看出经过了两次平移、一次旋转。具体的矩阵变换如下图：

从上面可以看出变换组合实际上就是组合各种变换矩阵，从而得到一个最终变换矩阵即可。

正交投影

​ 投影意味着降维操作。有一种投影方法是在某个方向上用零作为缩放因子，这种情况下，所有点都被拉平至垂直的轴（2D）或平面（3D）上，这种类型的投影称作正交投影，或者平行投影，因为从原来的点到投影点的直线相互平行

透视投影

​ 透视投影的投影线不在是平行的，它们相交于一点，该点称作投影中心。因为投影中心在投影平面前面，投影线到达平面之前已经相交，所以投影平面上的图像是翻转的。当物体远离投影中心时，正交投影任保持不变，但透视投影变小

参考文章：

旋转变换（一）旋转矩阵