DLSODE 计算微分方程组会遇到的一些问题解析
DLSODE是一个计算微分方程组的很好用用的程序包,在科研工作中常常会被使用,但是在使用当中会遇到一些小问题,总结如下,大家可以有兴趣看看:
如果某个程序直接拷贝到Microsoft Visual Studio Fortran的工程当中,编译会出现如下情况错误:

采用debug和release模式都不能解决,有些”If actual argument…dummy argument…”的问题是可以改为release模式消除的,但是如果想进行dubug模式来调试的话,这些错误无法克服,修改如下选项就可以实现调试:
项目,工程属性,Fortran,Diagnostics,选择 Check Routine Interfaces为 NO
基础知识:
Check Routine Interfaces:
IVF虚参和实参不一致,如何设置取消接口检查?
最近学习求解常微分方程的程序,从网上下了一个,但是程序里有一些用法是实参和虚参不一致,
这种用法在Powerstation4.0中可以正常运行,但是到了IVF中提示错误。
因为程序是老程序,模式比较固定,我目前是初学,修改起来比较费劲,所以我想求教一下:
有没有不修改程序,通过设置编译器的一些选项来是其在IVF里运行通过的。
补充一下程序段:
CALL SSTODE (NEQ, Y,RWORK(LYH), NYH, RWORK(LYH), RWORK(LEWT),
1 RWORK(LSAVF), RWORK(LACOR), RWORK(LWM), RWORK(LWM),
2 F, JAC,SPRJS, SSOLSS)
错误提示:
1 error #6633: The type of the actual argument differs fromthe type of the dummy argument. [RWORK] F:\fortran\LSODE example\OPKSMAIN.for 3443
工程属性,Fortran,Diagnostics,选择 Check Routine Interfaces 为 NO
程序中的例子:
EXTERNAL FEX, JEX
C INTEGER IOPT, IOUT, ISTATE, ITASK, ITOL, IWORK(23),LIW, LRW,
C * MF, NEQ
C DOUBLEPRECISION ATOL(3), RTOL, RWORK(58), T,TOUT, Y(3)
C NEQ = 3
C Y(1) = 1.D0
C Y(2) = 0.D0
C Y(3) = 0.D0
C T = 0.D0
C TOUT = .4D0
C ITOL = 2
C RTOL = 1.D-4
C ATOL(1) = 1.D-6
C ATOL(2) = 1.D-10
C ATOL(3) = 1.D-6
C ITASK = 1
C ISTATE = 1
C IOPT = 0
C LRW = 58
C LIW = 23
C MF = 21
C DO 40 IOUT = 1,12
C CALL DLSODE (FEX,NEQ, Y, T, TOUT, ITOL, RTOL, ATOL, ITASK,
C * ISTATE, IOPT, RWORK, LRW, IWORK,LIW, JEX, MF)
C WRITE(6,20) T, Y(1), Y(2), Y(3)
C 20 FORMAT(' At t =',D12.4,' y =',3D14.6)
C IF (ISTATE .LT.0) GO TO 80
C 40 TOUT = TOUT*10.D0
C WRITE(6,60) IWORK(11), IWORK(12), IWORK(13)
C 60 FORMAT(/' No. steps =',i4,', No. f-s =',i4,', No. J-s =',i4)
C STOP
C 80 WRITE(6,90) ISTATE
C 90 FORMAT(///' Error halt.. ISTATE =',I3)
C STOP
C END
C
C SUBROUTINE FEX (NEQ, T, Y, YDOT)
C INTEGER NEQ
C DOUBLEPRECISION T, Y(3), YDOT(3)
C YDOT(1) =-.04D0*Y(1) + 1.D4*Y(2)*Y(3)
C YDOT(3) =3.D7*Y(2)*Y(2)
C YDOT(2) = -YDOT(1)- YDOT(3)
C RETURN
C END
C
C SUBROUTINE JEX (NEQ, T, Y, ML, MU, PD, NRPD)
C INTEGER NEQ, ML, MU, NRPD
C DOUBLEPRECISION T, Y(3), PD(NRPD,3)
C PD(1,1) = -.04D0
C PD(1,2) = 1.D4*Y(3)
C PD(1,3) = 1.D4*Y(2)
C PD(2,1) = .04D0
C PD(2,3) = -PD(1,3)
C PD(3,2) = 6.D7*Y(2)
C PD(2,2) = -PD(1,2)- PD(3,2)
C RETURN
C END
C
C The output from thisprogram (on a Cray-1 in single precision)
C is as follows.
C
C At t = 4.0000e-01 y = 9.851726e-01 3.386406e-05 1.479357e-02
C At t = 4.0000e+00 y = 9.055142e-01 2.240418e-05 9.446344e-02
C At t = 4.0000e+01 y = 7.158050e-01 9.184616e-06 2.841858e-01
C At t = 4.0000e+02 y = 4.504846e-01 3.222434e-06 5.495122e-01
C At t = 4.0000e+03 y = 1.831701e-01 8.940379e-07 8.168290e-01
C At t = 4.0000e+04 y = 3.897016e-02 1.621193e-07 9.610297e-01
C At t = 4.0000e+05 y = 4.935213e-03 1.983756e-08 9.950648e-01
C At t = 4.0000e+06 y = 5.159269e-04 2.064759e-09 9.994841e-01
C At t = 4.0000e+07 y = 5.306413e-05 2.122677e-10 9.999469e-01
C At t = 4.0000e+08 y = 5.494530e-06 2.197825e-11 9.999945e-01
C At t = 4.0000e+09 y = 5.129458e-07 2.051784e-12 9.999995e-01
C At t = 4.0000e+10 y = -7.170603e-08 -2.868241e-13 1.000000e+00
C
C No. steps = 330, No. f-s = 405, No. J-s = 69======================================================================
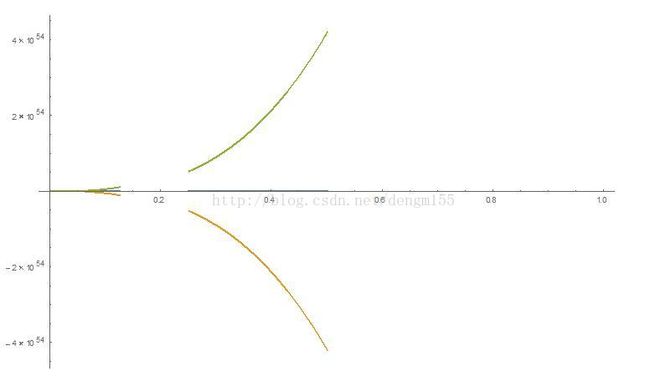
源程序代码,必须考虑到这是一个刚性问题,一下子就到了步数极限
NDSolve::ndsz: At t == 0.0014325942563598777`, step size iseffectively zero; singularity or stiff system suspected.>>
Input value {0.020428571428571428`} lies outsidethe range of data in the interpolating function. Extrapolation will be used.>>
例子当中的问题是个刚性系统问题,所以在程序中采用10模式,不需要雅克比函数,但是结果不准确,发散。
如果采用fm=10模式:
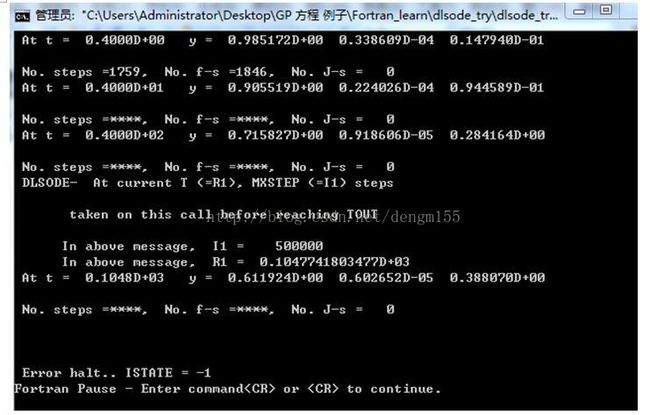
咋t=0.1048d+03就执行了500000步,尽管这几部得到的结果依旧还是没有错误的,但是很显然,演化时间很短就执行了极大的步数,使得程序结束,实际上,从前面mathmatic计算的结果可以看出来,如果不采用特殊的计算方法,计算结果也是发散的,错误的。
如果采用fm=21模式,则采用比如线性多步法求解,明显收敛,步数很少
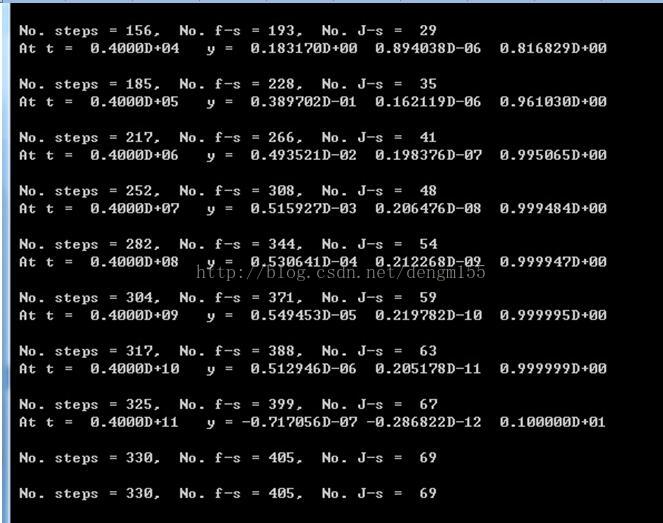
时间结束t=0.4d+11的时候,才执行330步,结果完美。所以对于刚性系统的话,fm=10的方法是不恰当的,包括mathmatic普通的NDSolve函数也是无法求解的。需要稍微注意下。