机器学习常用的numpy方法总结
文章目录
- np.mean()
- np.loadtxt()
- np.random.normal()
- np.where()
- np.ravel()&np.flatten()
- np.c_&np.r_
- np.meshgrid()
更新中~
np.mean()
求平均值,注意axis=0代表的是求每一列的平均值,axis=1是求每一行的平均值,这里的axis不要死记硬背,其实很容易记住,后面增加说明。不指定axis就默认对所有元素进行均值操作。
import numpy as np
a = np.arange(0, 20).reshape(4, -1)
print(a)
b = a.mean(axis=0)
print(b)
c = a.mean(axis=1)
print(c)
输出
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]]
[ 7.5 8.5 9.5 10.5 11.5]
[ 2. 7. 12. 17.]
那么高维的是啥情况呢?
import numpy as np
a = np.arange(0, 20).reshape(2, 2, -1)
print(a)
b = a.mean(axis=0)
print(b)
c = a.mean(axis=1)
print(c)
d = a.mean(axis=2)
print(d)
输出
[[[ 0 1 2 3 4]
[ 5 6 7 8 9]]
[[10 11 12 13 14]
[15 16 17 18 19]]]
[[ 5. 6. 7. 8. 9.]
[10. 11. 12. 13. 14.]]
[[ 2.5 3.5 4.5 5.5 6.5]
[12.5 13.5 14.5 15.5 16.5]]
[[ 2. 7.]
[12. 17.]]
可见axis控制了经过均值运算之后要消失的那个维度。axis为0的时候,行(第0维)会消失(加入计算最终合并成均值),只保留每一列的信息,所以是按列求均值。axis为2的时候,第三维的信息会消失,所以最后的结果是2x2的形式,2x2个结果中的每一个元素自然就是消失的那一维上每5个元素求一个平均值了。
np.loadtxt()
加载csv文件(csv从某种意义上说也属于txt文件),loadtxt主要的参数有delimiter和dtype。delimiter功能类似于split,一般csv文件的分隔符是逗号,演示如下,一共50行这样的数
data = np.loadtxt('./data.csv', delimiter=',')
读到的data的信息就是
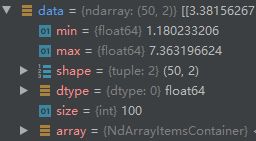
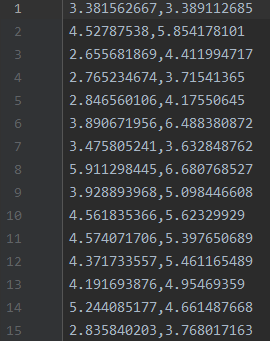
如果不设置任何参数,直接读这个文件,就会报错,因为loadtxt默认返回的是float类型的数据。而逗号也会被读到,所以就会报错,这时候就需要设置dtype来确定返回数据的类型。还是上面的文件,如果这么读取,就不会报错
data = np.loadtxt('./data.csv', dtype=str)
np.random.normal()
生成正态分布的数据,三个默认参数,第一个loc代表均值,第二个scale代表标准差,第三个size代表生成的数据分布的shape。
import numpy as np
a = np.random.normal(0, 1, (50, 50))
print(a.mean())
print(a.var())
输出为
-0.006853902270127236
1.0190338369486729
np.where()
简单的判别函数,但是注意返回值是一个元组,元组的第一个元素是array(索引),第二个元素是array中的数值类型
import numpy as np
y = np.array([1, 1, 0, 0, 1, 1])
pos = np.where(y == 1)
print(type(pos[0]))
print(type(pos))
print(pos)
输出
(array([0, 1, 4, 5], dtype=int64),)
如果是二维的,则一个array返回第一维坐标,一个array返回第二维坐标
import numpy as np
y = np.array([[1.0, 1.0, 0, 0, 1.0, 1.0], [1.0, 1.0, 0, 0, 1.0, 1.0], [1.0, 1.0, 0, 0, 1.0, 1.0]])
print(y)
pos = np.where(y == 1.0)
print(type(pos[0]))
print(type(pos))
print(pos)
输出为
[[1. 1. 0. 0. 1. 1.]
[1. 1. 0. 0. 1. 1.]
[1. 1. 0. 0. 1. 1.]]
(array([0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2], dtype=int64), array([0, 1, 4, 5, 0, 1, 4, 5, 0, 1, 4, 5], dtype=int64))
np.ravel()&np.flatten()
两个函数都是将多维的数组铺平成一维的数组,但是两者的区别是返回拷贝还是返回视图,就是说ravel返回的东西,修改后会影响原数组,flatten返回的东西,修改后就不会影响原数组。
np.c_&np.r_
np.r_是按列连接两个矩阵,就是把两矩阵上下拼接,要求列数相等。
np.c_是按行连接两个矩阵,就是把两矩阵左右拼接,要求行数相等。
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.c_[a,b]
print(np.r_[a,b])
print(c)
print(np.c_[c,a])
输出
[1 2 3 4 5 6]
[[1 4]
[2 5]
[3 6]]
[[1 4 1]
[2 5 2]
[3 6 3]]
np.meshgrid()
一般在分类结果可视化的时候常用,快速生成坐标矩阵,然后根据判别边界划分坐标矩阵中的所有的点。
x = np.linspace(0,1000,20)
y = np.linspace(0,500,20)
X,Y = np.meshgrid(x, y)
# 或者当已知x和y的范围的时候
x, y = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, h))
已知范围时x输出结果为:
array([[0.5 , 0.52, 0.54, ..., 7.34, 7.36, 7.38],
[0.5 , 0.52, 0.54, ..., 7.34, 7.36, 7.38],
[0.5 , 0.52, 0.54, ..., 7.34, 7.36, 7.38],
...,
[0.5 , 0.52, 0.54, ..., 7.34, 7.36, 7.38],
[0.5 , 0.52, 0.54, ..., 7.34, 7.36, 7.38],
[0.5 , 0.52, 0.54, ..., 7.34, 7.36, 7.38]])
y输出结果为:
array([[-0.4 , -0.4 , -0.4 , ..., -0.4 , -0.4 , -0.4 ],
[-0.38, -0.38, -0.38, ..., -0.38, -0.38, -0.38],
[-0.36, -0.36, -0.36, ..., -0.36, -0.36, -0.36],
...,
[ 2.94, 2.94, 2.94, ..., 2.94, 2.94, 2.94],
[ 2.96, 2.96, 2.96, ..., 2.96, 2.96, 2.96],
[ 2.98, 2.98, 2.98, ..., 2.98, 2.98, 2.98]])
之后生成一个一个坐标点
np.c_[xx.ravel(), yy.ravel()]
输出为
array([[ 0.5 , -0.4 ],
[ 0.52, -0.4 ],
[ 0.54, -0.4 ],
...,
[ 7.34, 2.98],
[ 7.36, 2.98],
[ 7.38, 2.98]])
然后依次判断每个坐标点属于哪一类,上色,之后画出来,判别边界就显得非常清晰了。
# z是每一个坐标点的类别,是一个一维array,按x的shape重排正好对应上
z = z.reshape(x.shape)
plt.pcolormesh(x, y, z, cmap=plt.cm.Paired)