图论入门

相关定义

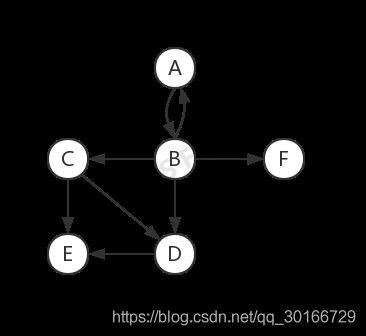
图 由顶点和边组成的结构
顶点 图中的元素节点，如上图中的A,B,C等
边(弧) 顶点之间的关系连线，如果边是有向(或者点对有序的)，则图也会被叫做有向图。
边的表示（A, B），同时也说明A，B邻接
度 顶点邻接的顶点数目

图的存储方式

1.邻接矩阵

对于上边的有向图，可以通过邻接矩阵的方式来表示：

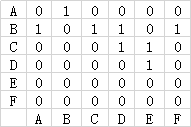
当图中顶点的度比较低时，我们说图是稀疏的，对应的矩阵也被称为稀疏矩阵

2.邻接表

当图是稀疏的时候，可以通过邻接表来表示：

对于每一个顶点，使用一个表来存放所有邻接的顶点

3. 图形结构的搜索

起点	0	1	0
0	0	0	0
0	0	1	0
0	1	终点	0
0	0	0	1

对应的邻接矩阵为：

/*
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
 */

3.1 深度优先搜索 DFS

从某个顶点A开始，遍历节点A的邻接顶点，在遍历过程中，递归调用深度优先搜索。
计算起点到终点的最短路径：

public class DepthFirstSearch {
    private static class Point {
        int x;
        int y;

        Point(int x, int y) {
            this.x = x;
            this.y = y;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Point point = (Point) o;
            return x == point.x &&
                    y == point.y;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y);
        }

        @Override
        public String toString() {
            return "Point{" +
                    "x=" + x +
                    ", y=" + y +
                    '}';
        }
    }

    // 表示5行4列
    static int m = 5, n = 4;

    // 用于保存顶点是否邻接
    private static int[][] values = new int[m][n];

    /// 用于标记顶点是否已经遍历
    private static boolean[][] marks = new boolean[m][n];

    // 表示方向，每次都会有上、下、左、右四个方向的节点
    private static int[][] direction = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

    private static Point targetPoint = new Point(3, 2);

    private static LinkedList<Point> stack = new LinkedList<>();

    private static Point[] minLoad;

    private static int minStep = Integer.MAX_VALUE;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                values[i][j] = scanner.nextInt();
            }
        }
        search(0, 0, 0);
        System.out.println("最短路径为" + minStep);
        System.out.println("最短路径为" + Arrays.toString(minLoad));
    }

    private static void search(int sourceX, int sourceY, int step) {
        Point sourcePoint = new Point(sourceX, sourceY);
        stack.push(sourcePoint);
        if (sourcePoint.equals(targetPoint) && step  < minStep) {
            minStep = step;
            minLoad = stack.toArray(new Point[]{});
            return;
        }
        for (int[] tem : direction) {
            int newX = sourcePoint.x + tem[0];
            int newY = sourcePoint.y + tem[1];
            // 判断顶点是否存在
            if (newX >= m || newX < 0 || newY >= n || newY < 0) {
                continue;
            }
            // 如果顶点不邻接
            if (values[newX][newY] == 1) {
                continue;
            }
            /// 如果顶点已遍历
            if (marks[newX][newY]) {
                continue;
            }
            // 避免重复查找
            marks[newX][newY] = true;
            search(newX, newY, step + 1);
            // 撤销查找标记
            marks[newX][newY] = false;
            stack.pop();
        }
    }
}

3.2 广度优先搜索 WFS

从某个顶点A开始，先遍历距离顶点A距离为1的顶点，再遍历距离顶点A距离为2的顶点(就是距离 与A的距离为1的顶点 为1的顶点)，直到遍历完所有顶点。
对与前边表中所示的图，如果要判断从起点是否可以抵达终点

public class BreadthFirstSearch {
    private static class Point {
        int x;
        int y;

        Point(int x, int y) {
            this.x = x;
            this.y = y;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Point point = (Point) o;
            return x == point.x &&
                    y == point.y;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y);
        }
    }

    // 表示5行4列
    static int m = 5, n = 4;

    // 用于保存顶点是否邻接
    private static int[][] values = new int[m][n];

    /// 用于标记顶点是否已经遍历
    private static boolean[][] marks = new boolean[m][n];

    // 表示方向，每次都会有上、下、左、右四个方向的节点
    private static int[][] direction = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

    public static void search(int sourceX, int sourceY, int targetX, int targetY) {
        Point sourcePoint = new Point(sourceX, sourceY);
        Point targetPoint = new Point(targetX, targetY);
        // 初始化一个队列
        Queue<Point> queue = new ArrayBlockingQueue<>(m * n);
        queue.offer(sourcePoint);
        marks[sourcePoint.x][sourcePoint.y] = true;
        while (!queue.isEmpty()) {
            Point point = queue.poll();
            if (point.equals(targetPoint)) {
                System.out.println("找到目标顶点");
                return;
            }
            // 将邻接的顶点添加到队列中
            for (int[] tem : direction) {
                int newX = point.x + tem[0];
                int newY = point.y + tem[1];
                // 判断顶点是否存在
                if (newX >= m || newX < 0 || newY >= n || newY < 0) {
                    continue;
                }
                // 如果顶点不邻接
                if (values[newX][newY] == 1) {
                    continue;
                }
                /// 如果顶点已遍历
                if (marks[newX][newY]) {
                    continue;
                }
                Point newPoint = new Point(newX, newY);
                queue.offer(newPoint);
            }
        }
        System.out.println("没有找到目标节点");
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                values[i][j] = scanner.nextInt();
            }
        }
        search(0, 0, 3, 2);
    }
}