SVD分解——>潜在语义分析LSA(I)——>概率性潜在语义分析PLSA(I)

SVD分解

1. 正交矩阵：若一个方阵其行与列皆为正交的单位向量，则该矩阵为正交矩阵，且该矩阵的转置和其逆相等。两个向量正交的意思是两个向量的内积为 0。
2. 正定矩阵：如果对于所有的非零实系数向量 $z$，都有$z^{T}Az>0$，则称矩阵$A$是正定的。正定矩阵的行列式必然大于 0，所有特征值也必然 > 0。相对应的，半正定矩阵的行列式必然 ≥ 0。

维基百科中对SVD的解释

假设有$m\times n$ 的矩阵 $A$ ，那么 SVD 就是要找到如下式的这么一个分解，将 $A$ 分解为 3 个矩阵的乘积：
$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T$$

其中，$U$ 和 $V$ 都是正交矩阵 （Orthogonal Matrix），在复数域内的话就是酉矩阵（Unitary Matrix），即

$$U^{T}U=E_{m\times m}$$

$$V^{T}V=E_{n\times n}$$

换句话说，就是说 $U$的转置等于 $U$ 的逆，$V$的转置等于 $V$ 的逆：

$$U^T=U^{-1}$$

$$V^T=V^{-1}$$

而 $\Sigma$ 就是一个非负实对角矩阵。

$U$ 和 $V$ 的列分别叫做 $A$ 的 左奇异向量（left-singular vectors）和 右奇异向量（right-singular vectors），$\Sigma$ 的对角线上的值叫做 $A$ 的奇异值（singular values）。

其实整个求解 SVD 的过程就是求解这 3 个矩阵的过程，而求解这 3 个矩阵的过程就是求解特征值和特征向量的过程，问题就在于 求谁的特征值和特征向量。

$U$ 的列由 $A{A}^T$的单位化过的特征向量构成
$V$ 的列由$A^{T}A$ 的单位化过的特征向量构成
$\Sigma$ 的对角元素来源于$A{A}^T$或$A^{T}A$ 的特征值的平方根，并且是按从大到小的顺序排列的
知道了这些，那么求解 SVD 的步骤就显而易见了：

求 $A{A}^T$的特征值和特征向量，用单位化的特征向量构成 $U$
求$A^{T}A$ 的特征值和特征向量，用单位化的特征向量构成 $V$
将$A{A}^T$ 或者 $A^{T}A$ 的特征值求平方根，然后构成 $\Sigma$

Numpy实现

import numpy as np

A = np.array([[2, 4], [1, 3], [0, 0], [0, 0]])
print(np.linalg.svd(A))

LSA(I)

LSA(latent semantic analysis)潜在语义分析，也被称为 LSI(latent semantic index)，是 Scott Deerwester, Susan T. Dumais 等人在 1990 年提出来的一种新的索引和检索方法。该方法和传统向量空间模型(vector space model)一样使用向量来表示词(terms)和文档(documents)，并通过向量间的关系(如夹角)来判断词及文档间的关系；不同的是，LSA 将词和文档映射到潜在语义空间，从而去除了原始向量空间中的一些“噪音”，提高了信息检索的精确度。

1. 矩阵 $U$ 的每一行表示一个词，每一列表示一个语义相近的词类，这一行中每个非零元素表示每个词在每个语义类中的重要性（或者说相关性）如$U=[0.7,0.15;0.22,0.49;0.3,0.03]$ ，则第一个词和第一个语义类比较相关，第二个词正好相反，第三个词与两个语义都不相关。
2. 矩阵 $V^T$ 是对文本进行分类的一个结果，它的每一行表示一个主题，每一列表示一个文本，这一列每个元素表示这篇文本在不同主题中的相关性。如$V=[0.7,0.15;0.22,0;0.92,0.08]$,则$V^T=[0.7,0.22,0.92;0.15,0,0.08]$第一篇文章属于第一个主题，第二篇文章和第二个主题非常相关，第三篇文章与两个主题都不相关
3. 矩阵 $D$ 表示词的类和文章的类之间的相关性如$DB=[0.7，0.21;0.18，0.63]$，则第一个词的语义类和第一个主题相关，和第二个主题没有太多关系，第二个词的语义类则相反

LSA详细流程：

（1）生成词汇库（以英文文本为例）： a从文本中过滤非英文字母字符; b过滤禁用词; c相同词根单词归一; d词汇统计和排序: e生成词汇库
(2)生成词汇-文本矩阵： 由各索引词在每篇文本中的出现频率生成词汇-文本矩阵 X 该矩阵中(第 i行第 j 列的元素数值aij 表示第 i个索引词在第 j 篇文本中出现的频率或者TF-IDF加权词频)。初始矩阵中每一行对应一个词，每列对应一篇文章，M个词和N篇文章可以表示为如下MX N的矩阵
（3）奇异值分解：a 对SVD分解后的矩阵进行降维; b使用降维后的矩阵构建潜在语义空间

LSA的优点

1）低维空间表示可以刻画同义词，同义词会对应着相同或相似的主题。
2）降维可去除部分噪声，使特征更鲁棒。
3）充分利用冗余数据。
4）无监督/完全自动化。
5）与语言无关。

LSA的缺点

1）LSA可以处理向量空间模型无法解决的一义多词(synonymy)问题，但不能解决一词多义(polysemy)问题。因为LSA将每一个词映射为潜在语义空间中的一个点，也就是说一个词的多个意思在空间中对于的是同一个点，并没有被区分。
2）SVD的优化目标基于L-2 norm 或者 Frobenius Norm 的，这相当于隐含了对数据的高斯分布假设。而 term 出现的次数是非负的，这明显不符合 Gaussian 假设，而更接近 Multi-nomial 分布。
3）特征向量的方向没有对应的物理解释。
4）SVD的计算复杂度很高，而且当有新的文档来到时，若要更新模型需重新训练。
5）没有刻画term出现次数的概率模型。
6）对于count vectors 而言，欧式距离表达是不合适的（重建时会产生负数）。

PLSA(I)

假设你要写M篇文档，由于一篇文档由各个不同的词组成，所以你需要确定每篇文档里每个位置上的词。再假定你一共有K个可选的主题，有V个可选的词，咱们来玩一个扔骰子的游戏。

1. 假设你每写一篇文档会制作一颗K面的“文档-主题”骰子（扔此骰子能得到K个主题中的任意一个），和K个V面的“主题-词项” 骰子（每个骰子对应一个主题，K个骰子对应之前的K个主题，且骰子的每一面对应要选择的词项，V个面对应着V个可选的词）。

比如可令K=3，即制作1个含有3个主题的“文档-主题”骰子，这3个主题可以是：教育、经济、交通。然后令V
=3，制作3个有着3面的“主题-词项”骰子，其中，教育主题骰子的3个面上的词可以是：大学、老师、课程，经济主题骰子的3个面上的词可以是：市场、企业、金融，交通主题骰子的3个面上的词可以是：高铁、汽车、飞机。

2. 每写一个词，先扔该“文档-主题”骰子选择主题，得到主题的结果后，使用和主题结果对应的那颗“主题-词项”骰子，扔该骰子选择要写的词。 {每篇文档有不同的 文档-主题 骰子}
   先扔“文档-主题”的骰子，假设（以一定的概率）得到的主题是教育，所以下一步便是扔教育主题筛子，（以一定的概率）得到教育主题筛子对应的某个词：大学。

上面这个投骰子产生词的过程简化下便是：“先以一定的概率选取主题，再以一定的概率选取词”。事实上，一开始可供选择的主题有3个：教育、经济、交通，那为何偏偏选取教育这个主题呢？其实是随机选取的，只是这个随机遵循一定的概率分布。比如3个主题的概率分布是{教育：0.5，经济：0.3，交通：0.2}，我们把各个主题z在文档d中出现的概率分布称之为主题分布，且是一个多项分布。

同样的，从主题分布中随机抽取出教育主题后，依然面对着3个词：大学、老师、课程，这3个词都可能被选中，但它们被选中的概率也是不一样的。比如3个词的概率分布是{大学：0.5，老师：0.3，课程：0.2}，我们把各个词语w在主题z下出现的概率分布称之为词分布，这个词分布也是一个多项分布。

所以，选主题和选词都是两个随机的过程，先从主题分布{教育：0.5，经济：0.3，交通：0.2}中抽取出主题：教育，然后从该主题对应的词分布{大学：0.5，老师：0.3，课程：0.2}中抽取出词：大学。

3. 最后，你不停的重复扔“文档-主题”骰子和”主题-词项“骰子，重复N次（产生N个词），完成一篇文档，重复这产生一篇文档的方法M次，则完成M篇文档。

在这个过程中，我们并未关注词和词之间的出现顺序，所以pLSA是一种词袋方法。具体说来，该模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别。

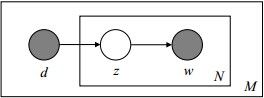
Note: 这个图的意思是，文档中的每一个词都是先选定一个主题，再从中选择词得到；文档中的每个词并不一定对应同一个主题z（z放在了小方框的里面了）
PLSA采用EM算法进行求解

pLSA的优势

1）定义了概率模型，而且每个变量以及相应的概率分布和条件概率分布都有明确的物理解释。
2）相比于LSA隐含了高斯分布假设，pLSA隐含的Multi-nomial分布假设更符合文本特性。
3）pLSA的优化目标是是KL-divergence最小，而不是依赖于最小均方误差等准则。
4）可以利用各种model selection和complexity control准则来确定topic的维数。

pLSA的不足

1）概率模型不够完备：在document层面上没有提供合适的概率模型，使得pLSA并不是完备的生成式模型，而必须在确定document i的情况下才能对模型进行随机抽样。
2）随着document和term 个数的增加，pLSA模型也线性增加，变得越来越庞大。
3）EM算法需要反复的迭代，需要很大计算量。

针对pLSA的不足，研究者们又提出了各种各样的topic based model, 其中包括大名鼎鼎的Latent Dirichlet Allocation (LDA)。