现代数字信号处理——维纳滤波原理及自适应算法

一、维纳滤波器基本理论

1、自适应横向滤波器

• $w_i^{\ast }$：滤波器权系数
• $w=[w_0,w_1,\cdots ,w_{M-1}]$：滤波器权向量
• $d(n)$：期望响应
• $\hat{d}(n)={\sum }_{i=0}^{M-1}{w}_i^{\ast }u(n-i)=w^{H}u(n)=u^T(n)w^{\ast }$：对期望响应的估计
• $e(n)=d(n)-\hat{d}(n)$：估计误差

2、均方误差准则

$$\begin{gathered} e(n)=d(n)-\hat{d}(n)=d(n)-w^{H}u(n)=d(n)-u^T(n)w^{\ast } \\ J(w)=E\{|e(n){|}^2\}=E\{e(n)e^{\ast }(n)\} \\ =E\{|d(n){|}^2\}-E\{d(n)u^H(n)\}w-w^{H}E\{u(n)d^{\ast }(n)\}+w^{H}E\{u(n)u^H(n)\}w \\ ={\sigma }_d^2-p^{H}w-w^{H}p+w^{H}Rw \end{gathered}$$

\quad $J(w)$是凸函数，且开口向上。

3、维纳-霍夫方程

\quad 如何求得最优权向量呢？因为$J(w)$是凸函数，因此对$J(w)$求导为0的结果就是答案。$$\begin{gathered} \Delta J(w)=-2p+2Rw=0 \\ R{w}_0=p \\ 因为R非奇异，最优权向量w_0=R^{-1}p \end{gathered}$$
\quad 这就是最小均方误差准则——使误差的平均功率最小。

4、正交原理

$$\begin{gathered} R{w}_0=p\to R{w}_0-p=0 \\ E\{u(n)u^H(n)\}{w}_0-E\{u(n)d^{\ast }(n)\}=0 \\ E\{u(n)[u^H(n)w_0-d^{\ast }(n)]\}=0 \\ E\{u(n)e_o^{\ast }(n)\}=0\to E\{u(n-i)e_o^{\ast }(n)\}=0 \end{gathered}$$

• 估计误差$e_0(n)$与所有抽头的输入信号$u(n-i)$相互正交
• $E\{{\hat{d}}_0(n)e_o^{\ast }(n)\}=w_o^{H}E\{u(n)e_o^{\ast }(n)\}=0$，所以${\hat{d}}_0与e_0(n)$也相互正交

5、最小均方误差

$$\begin{gathered} 当R{w}_0=p时J_{min}={\sigma }_d^2-p^H{w}_0={\sigma }_d^2-w_0^{H}R{w}_0 \\ ={\sigma }_d^2-w_0^{H}E\{u(n)u^H(n)\}{w}_0={\sigma }_d^2-w_0^{H}E\{[w_0^{H}u(n)][w_0^{H}u(n){]}^{\ast }\} \end{gathered}$$
\quad $J_{min}={\sigma }_d^2-E\{|\hat{d}(n){|}^2\}={\sigma }_d^2-{\sigma }_{\hat{d}}^2$，最小均方误差就是期望响应的平均功率与最优滤波器输出的估计信号的平均功率之差。

二、维纳滤波求解——最陡下降法

\quad 利用维纳霍夫方程求解需要计算矩阵$R$的逆，计算量大。沿着$J(w)$的负梯度方向调整$w$可以寻到最优权向量。$$\begin{gathered} w(n+1)=w(n)+\Delta w,\Delta w=-\frac{1}{2}\mu \Delta J(w(n)) \\ \Delta J(w(n))=-2p+2Rw \\ w(n+1)=w(n)+\mu [p-Rw(n)] \end{gathered}$$
\quad 如果步长因子满足$$0<\mu <\frac{2}{{\lambda }_{max}},{\lambda }_{max}为R的最大特征值$$，那么最陡下降法会逐步逼近极小值。
\quad 如果步长满足上述式子，则均方误差$J(n)$关于时间$n$是一个单调递减函数，且$li{m}_{n\to \infty }J(n)=J_{min}$。

三、随机梯度算法LMS

\quad 梯度下降算法缺点在于当$P,R$确定时，迭代过程和结果就确定了；与输入信号变换无关，不具有自适应性。
\quad 在LMS中，用n时刻的瞬时估计值$\hat{R}=u(n)u^H(n),\hat{p}=u(n)d^{\ast }(n)$代替统计量$R,p$，则可得$$\hat{\Delta }J(n)=-2\hat{p}+2\hat{R}w(n)=-2u(n)e^{\ast }(n)$$

LMS算法

• 1.初始化$n=0；权向量\hat{w}(0)=0；估计误差e(0)=d(0)-\hat{d}(0)=d(0)=0；输入向量u(0)=[u(0),u(-1),\cdots ,u(-M+1){]}^T=[u(0),0,\cdots ,0{]}^T$
• 2.对$n=0,1,2,\cdots$，$权向量更新\hat{w}(n+1)=\hat{w}(n)+\mu u(n)e^{\ast }(n)；期望信号估计\hat{d}(n+1)={\hat{w}}^H(n+1)u(n+1)；估计误差e(n+1)=d(n+1)-\hat{d}(n+1)$
• 3.令n=n+1，转到步骤2

\quad LMS算法的收敛条件与普通梯度下降相同，即$0<\mu <\frac{2}{{\lambda }_{max}},{\lambda }_{max}为R的最大特征值$。
\quad LMS算法的统计特性

• 均值$E\{\hat{J}(\infty )\}=J_{min}(1+\frac{\mu {\sum }_{i=1}^M{\lambda }_i}{2-\mu {\sum }_{i=1}^M{\lambda }_i})$，其中${\lambda }_i$是自相关矩阵$R$的全部特征值
• $\mu$满足不等式$0<\mu <\frac{2}{{\sum }_{i=1}^M{\lambda }_i}=\frac{2}{输入总功率}$，$r(0)$即为输入信号$u(n)$的总功率
• 剩余均方误差$J_{ex}(\infty )=E\{\hat{J}(\infty )\}-J_{min}$
• 失调参数$M=\frac{J_{ex}(\infty )}{J_{min}}=\frac{\mu {\sum }_{i=1}^M{\lambda }_i}{2-\mu {\sum }_{i=1}^M{\lambda }_i}$
• 平均时间常数表征LMS算法的平均收敛速度${\tau }_{av}=\frac{1}{2\mu {\lambda }_{av}}$，${\lambda }_{av}$为自相关矩阵R的特征值的平均值。
• 收敛速度不仅与步长有关，还与相关矩阵的特征值有关。定义$X(R)=\frac{{\lambda }_{max}}{{\lambda }_{min}}$，当$X(R)$非常大时，称R是病态的，其值越大，SD和LMS算法收敛速度越慢。

\quad 如果$\mu$增大，收敛速度增大，但稳态性能$M$变差。一般使用变步长，先大后小。

变步长LMS算法

\quad 步长$\mu (n)$随着$e(n)$的变化而变换：$\mu (n+1)=\alpha \mu (n)+\lambda |e(n){|}^2$

归一化LMS算法

\quad 可以有效避免LMS算法噪声放大的问题：$\hat{w}(n+1)=\hat{w}(n)+\frac{\mu }{|u(n){|}^2}u(n)e^{\ast }(n)$

泄露LMS算法

\quad 为了提升计算时的数值稳定性：$\hat{w}(n+1)=(1-\mu \alpha )\hat{w}(n)+\mu u(n)e^{\ast }(n),0<\alpha <1/\mu$

四、多级维纳滤波

\quad 对任意的非奇异变换矩阵$T_1\in C^{M\ast M}$作用于观测向量$u_0(n)$，有$z_1=T_1{u}_0(n)$。对观测数据$u_0(n)$进行可逆的满秩变换，不会改变维纳滤波器的估计输出和最小均方误差。

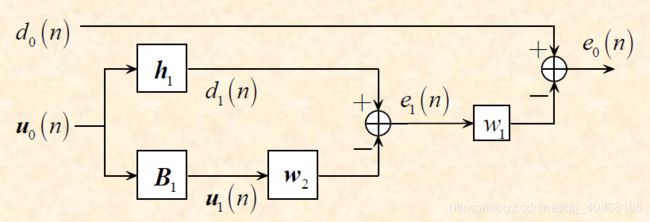
• $u_1(n)=B_1{u}_0(n),d_1(n)=h_1^H{u}_0(n)$
• $R_1=E\{u_1(n)u_1^H(n)\}=B_1{R}_0{B}_1^H$
• $p_1=E\{u_1(n)d_1^{\ast }(n)\}=B_1{R}_0{h}_1$
• $R_{1}w2=p_1(维纳霍夫方程)$
• ${\sigma }_{d1}^2=E\{|d_1(n){|}^2\}=h_1^H{R}_0{h}_1$
• ${\delta }_1=h_1^H{p}_0=||p_0||$
• $w_1=\frac{{\delta }_1}{{\sigma }_{d1}^2-p_1^H{R}_1^{-1}{p}_1}$
• 最小均方误差${\sigma }_{d1}^2-p_1^H{R}_1^{-1}{p}_1$

基于输入信号统计特性的权值计算步骤

构造阻塞矩阵

\quad 我们需要根据$h_m=[{\theta }_1,\cdots ,{\theta }_{M-m+1}]$构造阻塞矩阵$B_m$，使得$B_m{h}_m=0$，下图是一种构造：

基于观测数据的权值递推算法

\quad 基于观测数据统计特性的多级维纳滤波器权值递推中需要计算逆矩阵$R_m^{-1}$，这里给出无需计算逆矩阵的递推法。