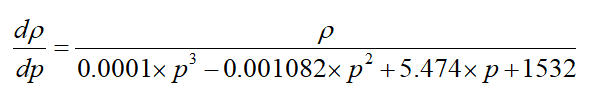matlab解常微分方程/进行数值积分/kmeans聚类分析

  在数学建模中我遇到了两个数学学习中常见的两个问题，即解常微分方程与数值积分。下面我们来看这两个问题怎么在matlab中得以解决。

  除此以外，数学建模中也经常遇到聚类分析，这里也举一个简单的例子。

1.使用ode45()解常微分方程的数值解

  【例】解微分方程

初值条件为p(70)=0.8384

【解】

druo=@(p,ruo)(ruo/(0.0001*p^3-0.001082*p^2+5.474*p+1532));
[p,ruo]=ode45(druo,[70 200],0.8384);
plot(p,ruo)
%%插值
p1=70:0.1:200;
ruo1=interp1(p,ruo,p1,'spline');

代码中的前两行是在使用ode45求解微分方程的数值解，没有什么特别好说明的，需要注意，习惯上。在“@（p,ruo）”这一部分中，自变量放在前，因变量放在后。

其中，第一行使用函数句柄定义了需要求解的方程，特别要注意的是调用格式[p,ruo]=ode45(druo,[70 200],0.8384);，在左边的大括号中，自变量放在前，因变量放在后，右边的部分，应该是ode45(函数句柄，[a b],c);其中a和c是对应的，a是初值条件中自变量的值，b是自己指定的任意区间右值，c是初值条件中因变量的值，在这里，由题目给出的初值条件p(70)=0.8384，可知，a=70，c=0.8384，b是自己随便指定的。

 

2.使用int()求解数值积分

直接给出代码

low=0;  up=5;%积分变量t的上下限

syms t;
p1 =    4.49e-13  ;
p2 =  -7.327e-11 ;
p3 =   9.172e-09  ;
p4 =  -6.245e-07 ;
p5 =  -0.0001539  ;p6 =     -0.1117  ;
p7 =       15.32  ;
Q = p1*t^6 + p2*t^5 + p3*t^4 + p4*t^3 + p5*t^2 + p6*t+ p7;

p1 =  -1.478e-09  ;
p2 =  -1.191e-06 ;
p3 =   0.0003362 ;
p4 =        0.85  ;
rho=p1*t^3+p2*t^2+p3*t+p4;


answer=int(rho*Q,t,low,up);
floor(answer)

【分析】

注意看代码内容，需要用syms t定义符号变量t，然后后面由大量内容只不过是定义了两个函数Q与rho。

事实上的积分，只需要一行代码

answer=int(rho*Q,t,low,up);

int（）的调用格式为int(符号函数,符号自变量,积分下限，积分上限)；

3.kmeans聚类分析

所谓聚类分析，就是把图像上离散的点分为离散的几类，其中内部的原理包含最小二乘法等内容，对于本科生来说没有必要了解其中的细节。

在使用时调用matlab中自带的kmeans函数即可，具体调用格式并不复杂，可以help kmeans查看