抽象代数笔记1——半群

本来想在知乎上写，后来想想，算了，拉低平均水平。。。

在知乎上找到一个不错的抽代笔记：
https://zhuanlan.zhihu.com/c_119426147?topic=%E6%8A%BD%E8%B1%A1%E4%BB%A3%E6%95%B0
可以参考。

我参考的是哈工大的近世代数课程和代数学引论。
开始没啥写的，就罗列一些概念吧：
(S, o) 代数系统， 其中o是二元代数运算: S x S -> S
如果满足结合律，就构成一个半群。

(S, o, e) 幺半群，存在左右幺元，（若存在，左右必相等）
（若存在2个左幺元，则不存在右幺元）

定理： 对于有限半群(S, o)，如果 ∃s，t∈S，sS=S，St=S. ∃ s ， t ∈ S ， s S = S ， S t = S .
那么它是 幺半群。
proof: s看为一个置换，那么显然有 sk=e s k = e ，故存在左幺元，
结论平凡。

如果一个幺半群 任意元素都有逆，那么就是群。

定理： 有限半群(S, o)是一个群，当且仅当
对于 ∀s∈S,sS=S ∀ s ∈ S , s S = S 并且 ∃t∈S,St=S. ∃ t ∈ S , S t = S .
proof: (S, o)是幺半群，于是 ∃n∈N+,∀s∈S,sn=e. ∃ n ∈ N + , ∀ s ∈ S , s n = e .
n=1 n = 1 时显然，否则 n≥2 n ≥ 2 ， s s 的逆为 sn−1 s n − 1 ，
于是所有元素可逆，(S, o)为群。

定理： (幺)半群(S, o)的 任意多个子(幺)半群 的交 仍是子(幺)半群
proof: 证明封闭性即可。

定义：(S, o)是一个(幺)半群，A是S的一个非空子集，
则S的一切包含A的子(幺)半群的交集(由上述定理知 是子(幺)半群)
称为由A生成的子(幺)半群，记为(A)
由(a)生成的子半群 {a,a2,...,an,...} { a , a 2 , . . . , a n , . . . } 是可交换的。

定义： 半群(S, o)的一个非空子集A称为S的一个左(右)理想，
如果 SA⊆A(AS⊆A) S A ⊆ A ( A S ⊆ A ) 。
如果A既是左理想，也是右理想，那么称A是S的理想。

易见： 左(右)理想的交仍是左(右)理想。
定义： (S, o)，A是S的一个非空子集。
S的 所有包含A的理想的交 称为 由A生成的理想。

定理： A是半群(S, o)的一个非空子集，
则：
1.由A生成的左理想是 A⋃SA A ⋃ S A
2.由A生成的右理想是 A⋃AS A ⋃ A S
3.由A生成的理想是 A⋃SA⋃AS⋃SAS A ⋃ S A ⋃ A S ⋃ S A S

定理： A是幺半群(M, o, e)的一个非空子集，则：
1. 由A生成的左理想是 MA
2. 由A生成的右理想是 AM
3. 又A生成的理想是 MAM

定义：
一个(幺)半群称为循环(幺)半群，如果这个(幺)半群是由其中的某个元素生成的(幺)半群。
由元素a生成的循环(幺)半群记为(a)
(即：证明 包含a的子(幺)半群是S，则S是循环(幺)半群)
(a)={a,a2,...,an,...}=S ( a ) = { a , a 2 , . . . , a n , . . . } = S
即：(a)生成的子半群是 由a的方幂构成的集合=S

定理：
循环(幺)半群 是 可交换(幺)半群。
proof: 循环半群是a的生成半群，可交换。

定义： 同构
设 (S,o) ( S , o ) 和 (T,∗) ( T , ∗ ) 是两个半群，如果存在从 S S 到 T T 的一个双射 φ φ ，
使得对 ∀a,b∈S ∀ a , b ∈ S
有 φ(a o b)=φ(a)∗φ(b) φ ( a   o   b ) = φ ( a ) ∗ φ ( b )
则称半群 (S,o) ( S , o ) 和 (T,∗) ( T , ∗ ) 同构。记为 (S,o)≅(T,∗) ( S , o ) ≅ ( T , ∗ ) 或 S≅T S ≅ T .
φ φ 称为从S到T的一个同构(映射)。
(有幺元时 φ(e)=e′ φ ( e ) = e ′ )

   
幺半群的Cayley定理：
任何幺半群 (M,o,e)  ( M , o , e )   同构于 变换幺半群 (L(M),o,lM) ( L ( M ) , o , l M )
proof:
构造 L(M)={ρa|ρa:M→M,a∈M,ρa(x)=a o x,∀x∈M} L ( M ) = { ρ a | ρ a : M → M , a ∈ M , ρ a ( x ) = a   o   x , ∀ x ∈ M }
即 L(M) L ( M ) 为这样一个集合，其元素是由 a a 所确定的 M M 上的一个左变换。
在 L(M) L ( M ) 上定义乘法 "o" " o " 如下：(映射的合成)
ρa o ρb=ρa o b,∀ρa,ρb∈L(M) ρ a   o   ρ b = ρ a   o   b , ∀ ρ a , ρ b ∈ L ( M ) ，
则 (L(M),o,ρe) ( L ( M ) , o , ρ e ) 是幺半群。
现在取 φ(a)=ρa φ ( a ) = ρ a ，易见同构。

定义： 同态
设 (S,o) ( S , o ) 和 (T,∗) ( T , ∗ ) 是两个半群，如果存在从 S S 到 T T 的一个映射 φ φ ，
使得对 ∀a,b∈S ∀ a , b ∈ S
有 φ(a o b)=φ(a)∗φ(b) φ ( a   o   b ) = φ ( a ) ∗ φ ( b )
则称半群 (S,o) ( S , o ) 和 (T,∗) ( T , ∗ ) 同态。 φ φ 称为从 S S 到 T T 的一个同态(映射)。

设 (M,o,e) ( M , o , e ) 和 (M′,∗,e′) ( M ′ , ∗ , e ′ ) 是两个幺半群，如果存在从 M M 到 M′ M ′ 的一个映射 φ φ ，
使得对 ∀a,b∈M ∀ a , b ∈ M ，有
φ(e)=e′, φ(a o b)=φ(a)∗φ(b) φ ( e ) = e ′ ,   φ ( a   o   b ) = φ ( a ) ∗ φ ( b )
则称幺半群 (M,o,e) ( M , o , e ) 和 (M′,∗,e′) ( M ′ , ∗ , e ′ ) 同态。 φ φ 称为从 M M 到 M′ M ′ 的一个同态(映射)。
(注： φ(e)=e′ φ ( e ) = e ′ 无法推出，在满同态下才行)

   
定理：
设 (S,o) ( S , o ) 是半群， (T,∗) ( T , ∗ ) 是代数系。
若存在 满射 φ:S→T φ : S → T 使得 ∀x,y∈S ∀ x , y ∈ S 有
φ(x o y)=φ(x)∗φ(y) φ ( x   o   y ) = φ ( x ) ∗ φ ( y )
则 T T 是半群。

定理：
设 (S,o,e) ( S , o , e ) 是幺半群， (T,∗) ( T , ∗ ) 是半群。
若 φ φ 是 S S 到 T T 的满半群同态，
则 φ(e) φ ( e ) 是 T T 的幺元，从而 (T,∗,φ(e)) ( T , ∗ , φ ( e ) ) 是幺半群。

定理：
设 (M,o,e) ( M , o , e ) 和 (M′,∗,e′) ( M ′ , ∗ , e ′ ) 是两个幺半群。
若 M M 到 M′ M ′ 有一个同态，
则 M M 的可逆元素 a a 的像 φ(a) φ ( a ) 也可逆，
并且 (φ(a))−1=φ(a−1) ( φ ( a ) ) − 1 = φ ( a − 1 )

   
同余关系定义：
设 ≅ ≅ 是代数系 (X,o) ( X , o ) 上的等价关系。
∀a,a′,b,b′∈X ∀ a , a ′ , b , b ′ ∈ X ，如果 a≅a′,b≅b′ a ≅ a ′ , b ≅ b ′ ，有 a o a′≅b o b′ a   o   a ′ ≅ b   o   b ′
那么就称 ≅ ≅ 是代数系 (X,o) ( X , o ) 上的同余关系。

定理：
设 ≅ ≅ 是代数系 (X,o) ( X , o ) 上的一个关系。
∀[a],[b]∈X/≅ ∀ [ a ] , [ b ] ∈ X / ≅ ，定义“ ⋅ ⋅ ”：
[a]⋅[b]=[a o b] [ a ] ⋅ [ b ] = [ a   o   b ]
则“ ⋅ ⋅ ”是 X/≅ X / ≅ 上的二元代数运算，当且仅当 ≅ ≅ 是同余关系。
(同余关系意味着从 X X 当中的乘法“ o o ”建立 X/≅ X / ≅ 当中的乘法“ ⋅ ⋅ ”)

定义：
设 (S,o) ( S , o ) 和 (T,∗) ( T , ∗ ) 是两个半群。 φ φ 是 S S 到 T T 的同态。
半群 (S/Eφ,⋅) ( S / E φ , ⋅ ) 称为 商半群。令 γ:S→S/Eφ,∀a∈S,γ(a)=[a] γ : S → S / E φ , ∀ a ∈ S , γ ( a ) = [ a ] ，则称 γ γ 为 S S 到商半群 S/Eφ S / E φ 的自然同态。

   

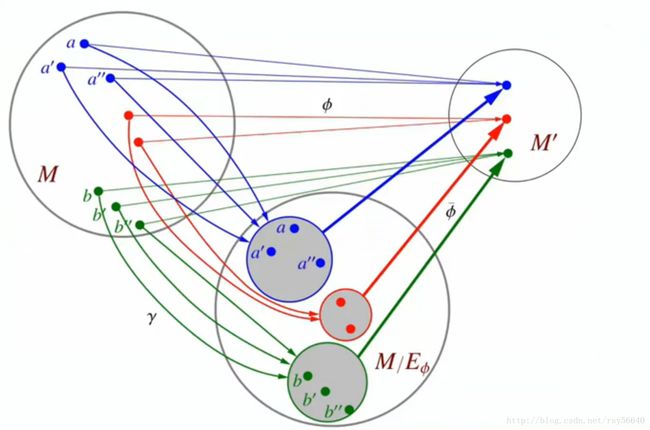
幺半群的同态基本定理：
设 φ φ 是幺半群 (M,o,e) ( M , o , e ) 到 (M′,∗,e′) ( M ′ , ∗ , e ′ ) 的同态，则：
1.同态像 φ(M) φ ( M ) 是 M′ M ′ 的一个子幺半群。
2.由 φ φ 确定的等价关系是同余关系。即如果 aEφa′,bEφb′ a E φ a ′ , b E φ b ′ ，那么 (a o b)Eφ(a′o b′) ( a   o   b ) E φ ( a ′ o   b ′ ) 。
于是 ∀[a],[b]∈M/Eφ,[a]⋅[b]=[a o b] ∀ [ a ] , [ b ] ∈ M / E φ , [ a ] ⋅ [ b ] = [ a   o   b ] 是 M/Eφ M / E φ 上的二元代数运算， (M/Eφ,⋅,[e]) ( M / E φ , ⋅ , [ e ] ) 是幺半群。
3.存在唯一的 M/Eφ M / E φ 到 M′ M ′ 的单同态 φ¯¯¯ φ ¯ 使得：
φ=φ¯¯¯ o γ φ = φ ¯   o   γ ，其中 γ γ 是 M M 到 M/Eφ M / E φ 的自然同态。
4.如果 φ φ 是满同态，则 M/Eφ M / E φ 与 M′ M ′ 同构。