CUDA学习笔记(LESSON3)——GPU基本算法(Part I)
CUDA系列笔记
CUDA学习笔记(LESSON1/2)——架构、通信模式与GPU硬件
CUDA学习笔记(LESSON3)——GPU基本算法(Part I)
CUDA学习笔记(LESSON4)——GPU基本算法(Part II)
CUDA学习笔记(LESSON5)——GPU优化
CUDA学习笔记(LESSON7)——常用优化策略&动态并行化
GPU基本算法(Part I)
步骤复杂度(step complexity)与工作量复杂度(work complexity)
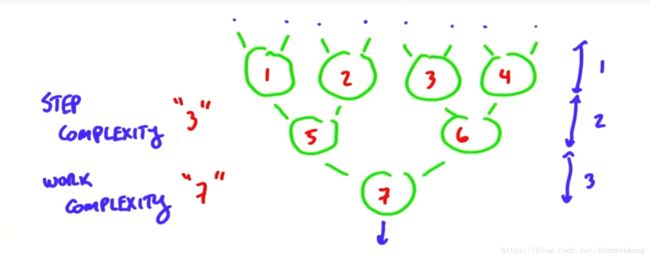
我们在讨论串行程序的算法复杂度是往往用时间复杂度这个指标衡量,也就是执行指令的条数,因为对于CPU来说,它运行的时间是与所执行指令的条数成正比的。而到并行算法中我们会考虑两个指标:step complexity与work complexity。step complexity指的是线程执行的步骤总共有多少,work complexity指的是考虑所有线程的工作量后计算出的复杂度。正是因为GPU具有并行计算的优势,使得许多工作我们可以同时完成,这就导致了程序的时间复杂度不再与work complexity相关,而是与step complexity相关
归约(Reduce)
Reduce要求输入一组元素,与一个二元操作符,这个二元操作符满足操作的结合性(例如加号),它的操作就是遍历这组元素,对每两个元素进行操作符运算。
我们可以实现reduce的串行版本,也就是最简单的累加操作,这个操作的step complexity与work complexity都是O(n)。显然这不适合GPU进行运算。
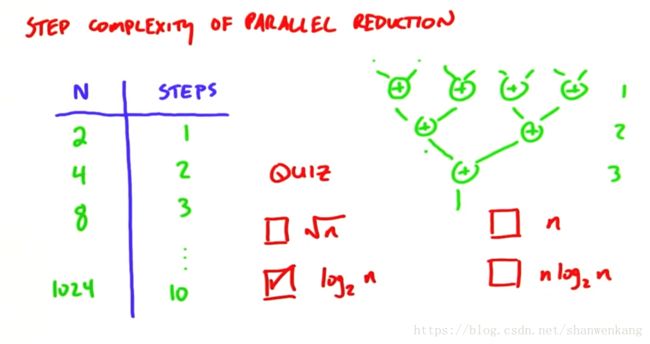
为了解决这个问题,我们需要reduce的并行版本,由于操作符具有结合性,因此我们可以通过结合不同的元素来达到相同的结果。我们采用二分的思想很容易得到下图所示的这种算法,这种算法的step complexity为O(logn),work complexity仍是原来的O(n),因为虽然步骤减少了,但是总共进行的操作数是不变的。
扫描(Scan)
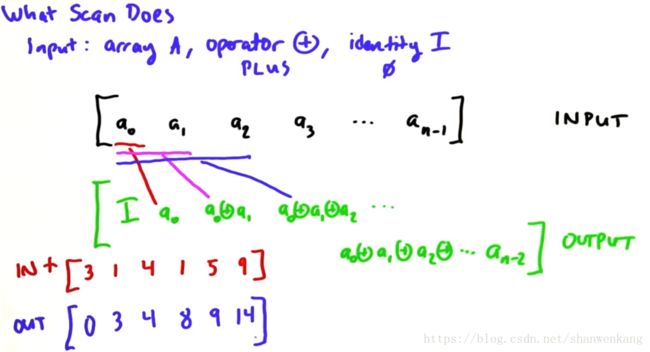
scan的操作有点类似reduce,它的作用对当前元素之前的所有元素进行操作符运算(例如相加),之后输出。scan在并行世界中非常有用,具体的例子我在下一个博客再写。
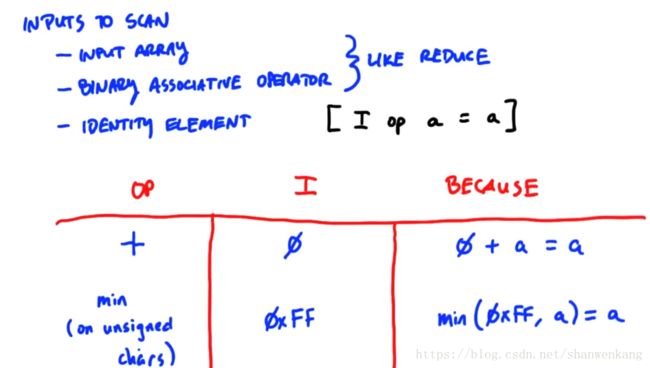
scan除了像reduce要求输入的元素与一个二元操作符以外还要求一个标识元素(identity element),一个元素与标识元素进行操作会得到他的本身。这个元素主要作为第一个输入元素的输出。
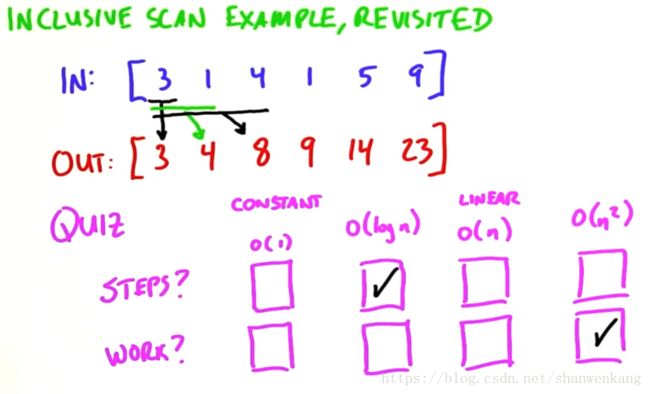
scan一般分为两种:exclusive scan和inclusive scan。顾名思义,exclusive就是进行操作符运算的所有元素不包括当前输入元素,inclusive就是进行操作符运算的所有元素包括当前输入元素。当我们将scan算法的时候,如果我们仔细去想,我们似乎很难想到它在并行世界中是如何实现的。
在看dalao的算法们之前我们先来看看一种比较蠢的算法。既然scan是对输入元素之前的所有元素进行reduce运行,那我们就给每一个元素安排一个线程,来计算它之前元素的归约结果,这种方法也确实是一种并行的实现啊。但是我们来分析一下它的复杂度呢。我们会发现它的step complexity为O(logn),嗯...看起来还不错。但是work complexity确是O(n^2),这就不太令人满意了。
下面来看看dalao们的想法,我们主要说两种,一种是Hillis&Steele的算法,一种是Blelloch的算法,其中前者在step complexity上表现得更好,而后者在work complexity上表现更好。
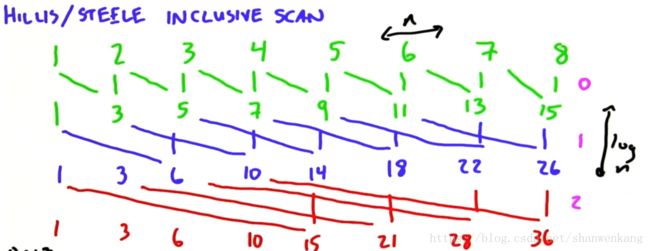
Hillis&Steele
以下就是Hillis&Steele的算法,它的结果是inclusive的,它的主要思想就是将每个元素与右边相邻的第1个元素相加,得到一组新的元素,再将每个元素与右边相邻的第2个元素相加,如此反复一直到将每个元素与右边相邻的第logn个元素相加以后输出的就是最终的inclusive scan的结果。这种算法的step complexity是O(logn),work complexity是O(nlogn),我们可以看出这种算法与前一种算法相比提升了work complexity的性能。
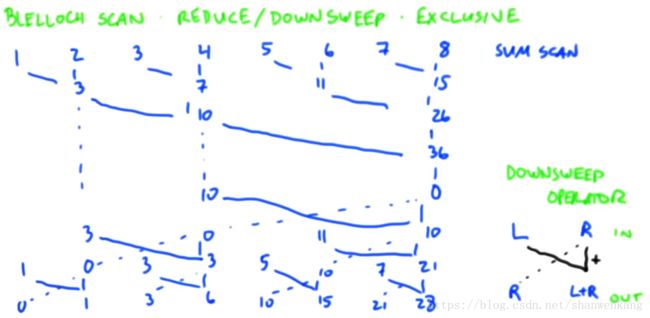
Blelloch
以下是Blelloch的算法,它的结果是exclusive的,这个算法包括两个部分:reduce与downsweep。downsweep的操作已经在下图右方给出。这种算法的复杂度为:reduce与downsweep的step分别有logn步,reduce的work complexity为O(n),downsweep的work complexity也为O(n),因此合起来Blelloch的算法step complexity为O(2logn),work complexity为O(2n)。
因此我们最终可以得出结论,在渐进的意义上,如果考虑常数项的影响,Hillis&Steele的算法的step complexity为O(logn)是要优于Blelloch算法的O(2logn),而work complexity上面,Blelloch算法的O(2n)优于Hillis&Steele算法的O(nlogn)。
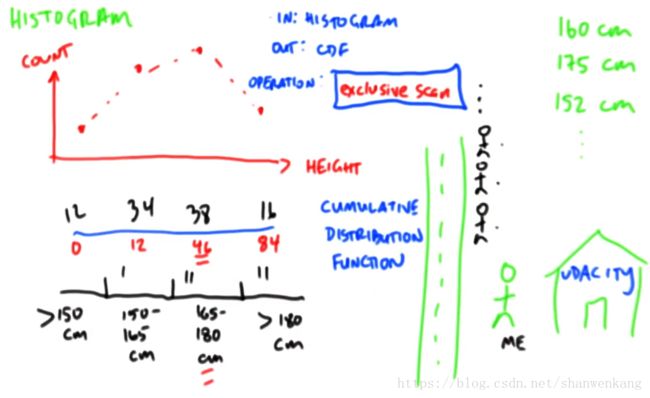
直方图(Histogram)
Histogram就是我们平时理解的直方图,也就是把输入数据进行分类,放到不同的计数器中,不同的计数器代表不同的区间范围,最终将计数器的值进行输出。我们将这个计数器称作bin。让我们想想办法如何去实现histogram呢?
第一种方法是最容易想的,就是bin放在global memory中,开启等同于元素个数的线程来读取数据,然后写入bin中。但这会出现一个严重的问题,就是线程冲突,这个问题我们在上一章已经讨论过,解决的方法就是采用atomic操作,来保护memory。这种方法速度严重受限于bin的数目,当bin比较少的时候,大多数线程不得不处在等待中,这大大地浪费了GPU的资源。因此我们说这并不是一种很好的方法。
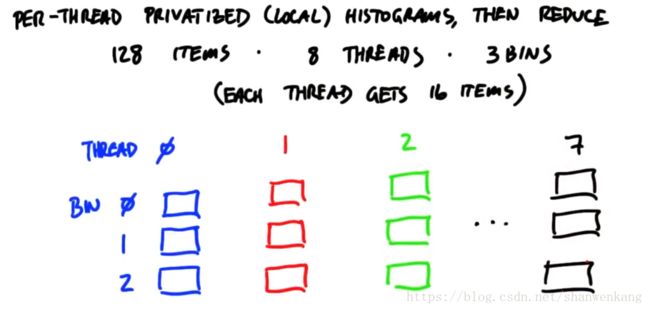
第二种实现方法就是我们在每一个线程中开辟一个local histogram,这样子就避免了对公共内存访问的冲突,在每个线程各自执行完自己的任务以后我们再把local histogram用reduce的方法加起来,合成最终的histogram
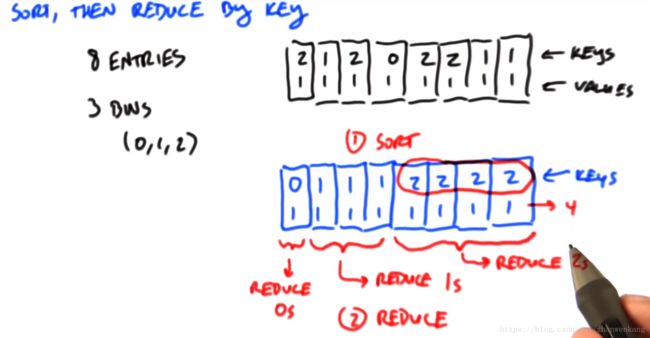
第三种方法是用sort+reduce来实现,我们给每一个元素建立一个map,key值为bin的索引,value值为二元值,代表这个元素归属这个bin中,之后我们用对其以key值的顺序大小进行排序,排序之后我们就可以用reduce方法计算出每个bin中有多少个元素了,注意这个时候元素的存储是连续的,因此在访问的时候也具有很高的效率。
当然我们也可以将这三种方法结合起来使用,以满足不同场景的不同需求。