二分图的最大匹配——匈牙利算法

二分图

简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。
也就是说，把一个图的顶点划分为两个不相交集 X 和 Y ，使得每一条边都分别连接 X 、 Y 中的顶点。如果存在这样的划分，则此图为一个二分图。

二分图的一个等价定义是：不含有「奇数条边的环」的图。

图 1 不含有「奇数条边的环」我们习惯上将其画成下列形式：

可以看到图 2 中每条边的两个端点属于不同的集合，这样的图就是一个二分图。
（并且我们人为约定，左边的点属于 X 集合，右边的点属于 Y 集合）

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。

例如，图 3 、图 4 中红色的边就是图 2 的匹配。

二分图的匹配

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点。 1−5、4−7 为匹配边，其他边为非匹配边。

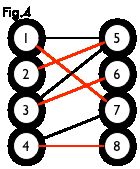
1. 最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。
2. 完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。
   图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

这两个概念应该十分明确，举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。
是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。
如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

匈牙利算法

二分图的最大匹配可以转换为一个网络流的问题，但是我们一般使用匈牙利算法，这种算法更易于理解，方便编写。
介绍这个算法之前，首先要介绍一些必要的概念。

1. 交错路 ： 从一个未匹配点出发，依次遍历未匹配边、匹配边、未匹配边，这样交替下去，这条路径称为交错路。

2. 增广路 ： 从一个未匹配点出发，依次遍历未匹配边、匹配边、未匹配边，这样交替下去，如果最后一个点是未匹配点，这条路径称为增广路。换句话说，起点和终点都为未匹配点的交错路为增广路（特别提醒，这里的增广路和网络流中的增广路的意义不同）

如图所示，图 6 是图 5 的其中一条增广路，可以看出由未匹配点 9 出发，依次沿着边 edge(9,4)−>edge(4,8)−>edge(8,1)−>edge(1,6)−>edge(6,1) 到达未匹配点 1 ，显然，这是一条增广路。

观察图 6 我们可发现增广路的一些特点。

1. 增广路一定有奇数条边。

2. 增广路中未匹配边一定比匹配边多一条（因为是从未匹配点出发走交错路到未匹配点结束）

这里其实就表明了研究增广路的意义。
如果找到了一条增广路，那么将未匹配点与匹配边的身份调换,那么匹配的边数就多了一条，这样直到找不到增广路为止，那么整个图的匹配的边数一定最大，也就是找到了二分图的最大匹配。

这里的身份调换是指 ：
原来匹配的边为 edge(1,6),edge(4,8) ，匹配边数为 2 。找到一条增广路（这里不一定从 9 开始找，任何一个未匹配点都可以）后，现在匹配的边为 edge(2,6),edge(1,8),edge(4,9) ,匹配边数为 3 。

匈牙利算法正是利用了增广路的这个性质，从 X 集合中找到一个未匹配点，寻找增广路，找到了匹配数+1，如果没有找到，那么从 X 中找到下一个未匹配的点，再次寻找增广路……重复上述过程，直到 X 集合中的所有节点都被“增广”完毕，无论如何都找不到增广路，那么整个图的匹配数就最大了。

下面给出匈牙利算法的伪代码 ：

void hungary()//匈牙利算法
{
    for i->1 to nx//对于集合X中的每一个节点
        if (从未匹配点i出发有增广路)
            匹配数++;
    输出 匹配数;
}
bool findpath(x)//寻找从x出发的对应项出的可增广路
{
    //crossPath[x] = true;这条语句可能会有很多人加上，但是实际上crossPtah总是记录集合Y中的节点是否在交错路上
    for each edge(x,y) in G.E
    {
        if(y is not in crossPath)
        {
            add y into crossPath
            lastX = match[y];//lastX是X集合的上一个与y匹配的节点
            if(y is not matched or findpath(lastX))//如果y已经被了，那么试试从lastX能不能另外找到一条增广路,把当前增广路让给现在的x
            {
                match[y] = x;
                //match[x] = y,wrong !
                return true;//从x出发有增广路
            }
        }
    }
    return false;//从x出发没有增广路
}

时间复杂度 ： 对于每一个属于集合X的节点x，调用 findpath(x) ,最坏情况下 findpath(x) 会遍历所有的边，所以该事件复杂度为 O(V*E)。

推荐两个模板题目 ：

hdu 2063
poj 1469

并且给出hdu 2063当做模板 ：

#include 
#include 
#pragma comment(linker,"/STACK:1024000000,1024000000")
const int maxn = 505;
const int maxm = 1005;
/*使用G++交题*/
struct Edge
{
    int to,next;
};
Edge edge[maxn];
int head[maxn],tot;
int match[maxn],ans;//match[x] = y表示x的匹配是y
bool inCrossPath[maxn];//在交错路中
int k,m,n;

void Init()
{
    memset(match,-1,sizeof(match));
    memset(head,-1,sizeof(head));
    tot = 0;
    ans = 0;
}
void addEdge(int u,int v)
{
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;
}
bool findpath(int u)
{
    int v;

    for(int i = head[u] ; i != -1 ; i = edge[i].next){
        v = edge[i].to;
        if(inCrossPath[v] == false){
            inCrossPath[v] = true;
            if(match[v] == -1 || findpath(match[v])){
                match[v] = u;
                return true;
            }
        }
    }
    return false;//千万别忘了这句
}
void Hungary()
{
    for(int i = 1 ; i <= m ; ++i){//只有女生有选择的权利,女生相当于X集合
        memset(inCrossPath,false,sizeof(inCrossPath));//每次清空交错路径
        if(findpath(i))
            ans++;
    }
}
int main()
{
    int u,v;
    while(scanf("%d",&k) != EOF && k){
        Init();
        scanf("%d%d",&m,&n);
        for(int i = 1 ; i <= k ; ++i){
            scanf("%d%d",&u,&v);
            addEdge(u,v);
        }
        Hungary();
        printf("%d\n",ans);
    }
    return 0;
}

推荐几个经典的例题，做完之后差不多就入门了 ：

poj 1274 (基础)
poj 2446 (建图特殊)
hdu 1281 (建图特殊)
hdu 2819 (难)

二分图最大匹配的扩展

1. 最大独立集 ： 二分图中最大的一个点集，该点集内的点互不相连（没有边相连）。回想一下图 4 : 显然这里给出了图的一个最大匹配，将最大匹配中的点从原来的节点集合 V 中删除，那么剩下的点不会有任何边相连，也就是说

   最大独立集数目=|V|−最大匹配数

2. 最小顶点覆盖 ：二分图中，用最少的点，让所有的边至少和一个点有关联。很显然，最大匹配中的结点满足该性质，也就是说

   最小顶点覆盖数=最大匹配数

3. 最小路径覆盖：在有向图中找一些路径，这些路径覆盖图中所有的顶点，每个顶点都只与一条路径相关联。在所有的路径覆盖中，路径个数最小的就是最小路径覆盖。

   最小路径覆盖=最大独立集=|V|−最大匹配

以上三条的正确性都不予证明…证明也会是很数学的东西，当做结论记起来就好。

练习题目 ：

poj 2060
poj 3041
poj 2226

本文图片摘自

http://www.renfei.org/blog/bipartite−matching.html