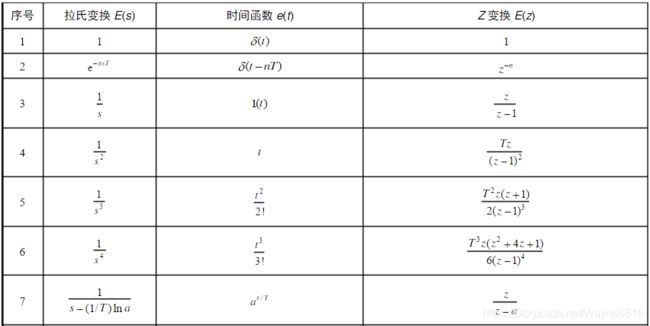
数形结合拉普拉斯变换【直观解释】—复变函数与积分变换学习笔记
本文用于学习中的记录,会在复习的过程中不断修订。
What is 拉普拉斯变换?
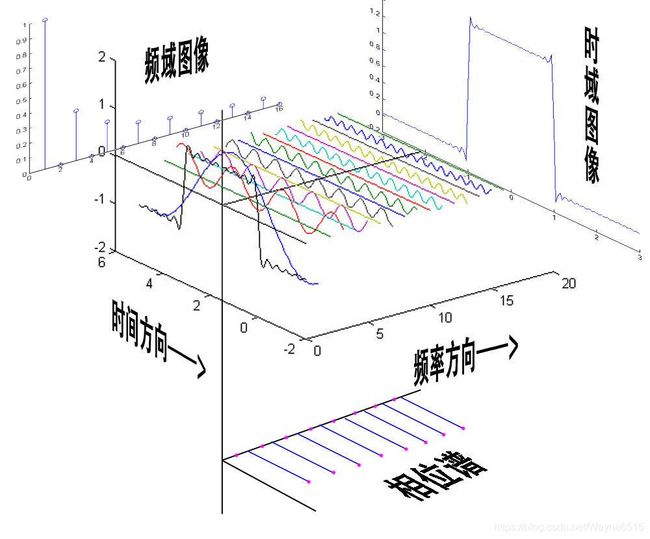
先放一张Matlab绘制的很有立体感的图,我们后面会了解。

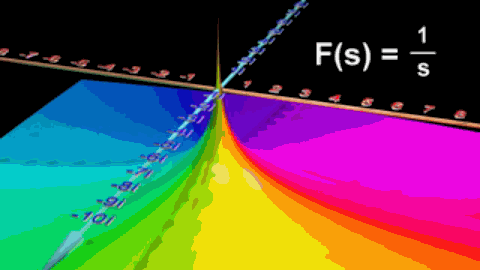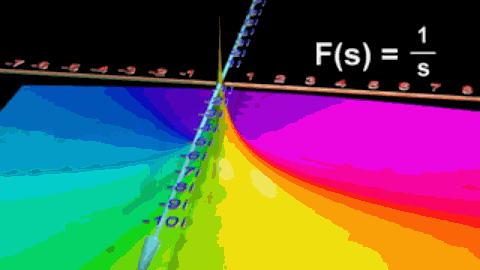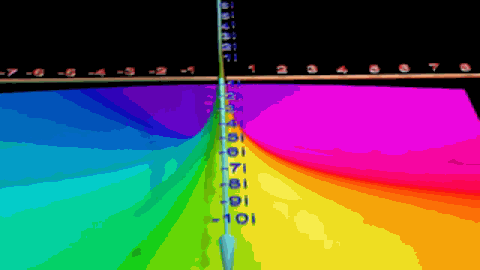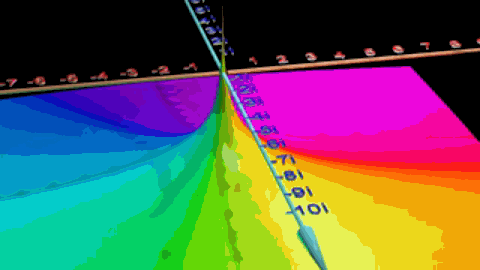
初学时我可看不大明白,因为得先明白什么是傅里叶变换,再放图
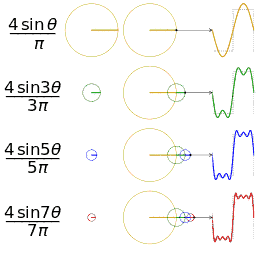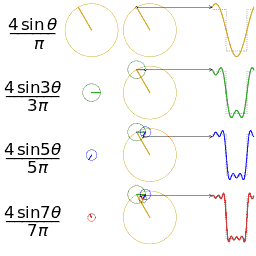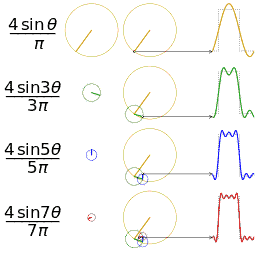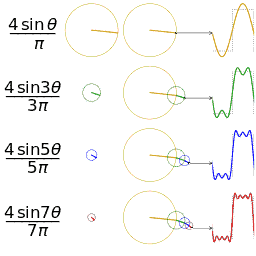
傅里叶变换的真理就是任何一个原始的周期性(非周期性可以由周期函数在T趋于 ∞ \infty ∞时变成非周期)函数,可以由多个正余弦波叠加来近似。它实质是是频域函数和时域函数的转换
一.
引入拉氏变换的实际背景:
傅氏变换必须在整个实轴上有定义,但在工程实际问题中,许多以时间t为自变量的函数在时间t<0时是无意义的。通常在信号与系统中用到的就是这种单边拉普拉斯变换(有时也将t=0_考虑进去),也就是因果系统(含有输入信号和输出信号的信号系统)的拉氏变换。
1.1定义
傅里叶正变换:
F ( ω ) F(ω) F(ω) = F [ f ( t ) ] \mathscr{F}[f(t)] F[f(t)] = ∫ − ∞ + ∞ f ( t ) e − j ω t d t \int_{-\infty}^{+\infty} f(t)e^{-jωt}dt ∫−∞+∞f(t)e−jωtdt
在傅氏变换的基础上,去掉t<0时的实轴范围,并对于复参数s=β+jω,
则有积分:
F ( S ) F(S) F(S) = L [ f ( t ) ] \mathscr{L}[f(t)] L[f(t)] = ∫ 0 + ∞ f ( t ) e − s t d t \int_0^{+\infty} f(t)e^{-st}dt ∫0+∞f(t)e−stdt
我们称F(s)是f(t)的拉普拉斯变换
反之f(t)是F(s)的拉普拉斯逆变换
例:
我们引入一个单位阶跃函数 u ( t ) u(t) u(t)(初学复变时做题经常不认识了的函数),来求它的拉氏变换。
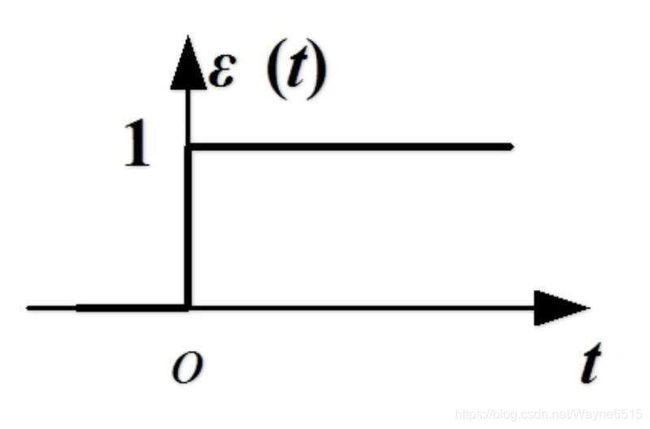
得
L [ u ( t ) ] = ∫ 0 + ∞ u ( t ) e − s t d t = 1 s ( R e s > 0 ) \mathscr{L}[u(t)]=\int_0^{+\infty}u(t)e^{-st}dt=\frac{1}{s}\qquad(Re s > 0) L[u(t)]=∫0+∞u(t)e−stdt=s1(Res>0)
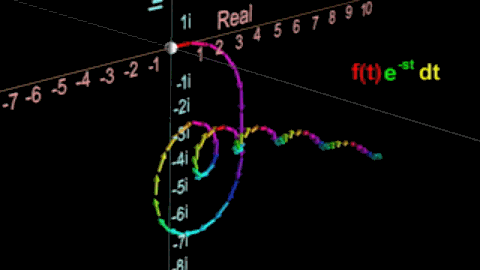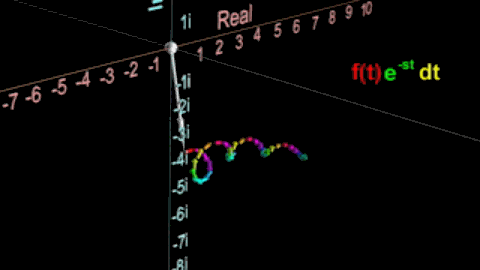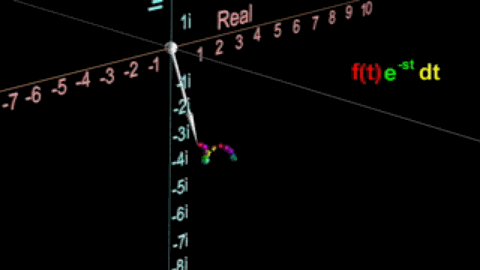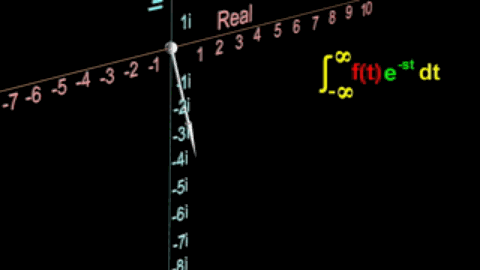
用数形结合来表示:
图中彩色螺旋即 e − s t e^{-st} e−st,现在令 f ( t ) = u ( t ) f(t)=u(t) f(t)=u(t),用阶跃函数来乘 e − s t e^{-st} e−st
得出来的结果如图

这时再取积分就得到了如下图中白色箭头所指的值 1 s \frac{1}{s} s1,也就是特定值s的拉普拉斯变换值。
但如果这个积分的结果是无限,那么我们就认为该特定值为s时,函数的波形不存在拉普拉斯变换,因为当s的实部为一个趋于无穷小的负数,则会出现这样的情况
积分结果将会是无穷大,所以去掉s < 0的区域,这样一来一开始的那张图就变成了
1.2与傅氏变换的关系
通过刚才引入的阶跃函数 u ( t ) u(t) u(t)我们就能将积分上下限换为负无穷到正无穷,并找到拉氏变换和傅氏变换的关系了。
即
F ( S ) F(S) F(S) = = = L [ f ( t ) ] \mathscr{L}[f(t)] L[f(t)] = = = ∫ 0 + ∞ f ( t ) e − s t d t \int_0^{+\infty} f(t)e^{-st}dt ∫0+∞f(t)e−stdt = ∫ − ∞ + ∞ f ( t ) u ( t ) e − β t ⋅ e − j ω t d t \int_{-\infty}^{+\infty}f(t)u(t)e^{-βt}·e^{-jωt}dt ∫−∞+∞f(t)u(t)e−βt⋅e−jωtdt \qquad (1)
\,\,\,\,\,\,\,\,\quad = = = F ( β + j ω ) F(β+jω) F(β+jω) = = = L [ f ( t ) u ( t ) e − β t ] \mathscr{L}[f(t)u(t)e^{-βt}] L[f(t)u(t)e−βt] \qquad\qquad\qquad\qquad\qquad
傅里叶逆变换:
f ( t ) f(t) f(t) = = = 1 2 π ∫ − ∞ + ∞ F ( ω ) e j ω t d ω \frac{1} {2π}\int_{-\infty}^{+\infty}F(ω)e^{jωt}dω 2π1∫−∞+∞F(ω)ejωtdω
将式1代入傅氏逆变换有
f ( t ) u ( t ) e − β t = 1 2 π ∫ − ∞ + ∞ F ( β + j ω ) e j ω t d ω f(t)u(t)e^{-βt}=\frac{1}{2π}\int_{-\infty}^{+\infty}F(β+jω)e^{jωt}dω f(t)u(t)e−βt=2π1∫−∞+∞F(β+jω)ejωtdω
两边同乘 e j ω t e^{jωt} ejωt,并令s=β+jω
则有
f ( t ) u ( t ) = 1 2 π j ∫ β − j ∞ β + j ∞ F ( s ) e s t d s f(t)u(t)=\frac{1}{2πj}\int_{β-j\infty}^{β+j\infty}F(s)e^{st}ds f(t)u(t)=2πj1∫β−j∞β+j∞F(s)estds
阶跃函数u(t)也就是t>0式为1,去掉
即拉普拉斯变换的反演积分公式 f ( t ) = 1 2 π j ∫ β − j ∞ β + j ∞ F ( s ) e s t d s f(t)=\frac{1}{2πj}\int_{β-j\infty}^{β+j\infty}F(s)e^{st}ds f(t)=2πj1∫β−j∞β+j∞F(s)estds ( t > 0 ) \qquad(t>0) (t>0)
二.
总结一些重要性质(其实大部分也就是微积分)
2.1 线性性质
L [ α f ( t ) + β g ( t ) ] = α F ( s ) + β G ( s ) \mathscr{L}[αf(t)+βg(t)]=αF(s)+βG(s) L[αf(t)+βg(t)]=αF(s)+βG(s)
L − 1 [ α F ( t ) + β G ( t ) ] = α f ( t ) + β g ( t ) \mathscr{L}^{-1}[αF(t)+βG(t)]=αf(t)+βg(t) L−1[αF(t)+βG(t)]=αf(t)+βg(t)
应用:可以快速求解 cos ω t \cosωt cosωt和 sin ω t \sinωt sinωt的拉氏变换
2.2 相似性质
L [ f ( α t ) ] = 1 α F ( s α ) \mathscr{L}[f(αt)]=\frac{1}{α}F(\frac{s}{α}) L[f(αt)]=α1F(αs)
2.3 微分性质
导数的像函数:
L [ f ′ ( t ) ] = s F ( s ) − f ( 0 ) \mathscr{L}[f'(t)]=sF(s)-f(0) L[f′(t)]=sF(s)−f(0)
L [ f ( n ) ( t ) ] = s n F ( s ) − s n − 1 f ( 0 ) − s n − 2 f ′ ( 0 ) − ⋅ ⋅ ⋅ − f ( n − 1 ) ( 0 ) \mathscr{L}[f^{(n)}(t)]=s^{n}F(s)-s^{n-1}f(0)-s^{n-2}f'(0)-\,···\,-f^{(n-1)}(0) L[f(n)(t)]=snF(s)−sn−1f(0)−sn−2f′(0)−⋅⋅⋅−f(n−1)(0)
应用:求解微分方程组的初值问题;求解幂函数 f ( t ) = t m f(t)=t^m f(t)=tm之类的拉氏变换
像函数的导函数:
F ′ ( s ) = − L [ t f ( t ) ] F'(s)=-\mathscr{L}[tf(t)] F′(s)=−L[tf(t)]
F ( n ) ( s ) = ( − 1 ) n L [ t n f ( t ) ] F^{(n)}(s)=(-1)^{n}\,\mathscr{L}[t^nf(t)] F(n)(s)=(−1)nL[tnf(t)]
应用:求 t sin ω t t\sinωt tsinωt、 t 2 c o s 2 t t^2cos^2t t2cos2t之类的拉氏变换
2.4 积分性质
积分的像函数:
L [ ∫ 0 t f ( t ) d t ] = 1 s F ( s ) \mathscr{L}[\int_0^tf(t)dt]=\frac{1}{s}F(s) L[∫0tf(t)dt]=s1F(s)
L ∫ 0 t d t ∫ 0 t d t ⋅ ⋅ ⋅ [ ∫ 0 t f ( t ) d t ] = 1 s n F ( s ) \mathscr{L}{\int_0^tdt}{\int_0^tdt\,···\,}[\int_0^tf(t)dt]=\frac{1}{s^n}F(s) L∫0tdt∫0tdt⋅⋅⋅[∫0tf(t)dt]=sn1F(s)
应用:求函数 f ( t ) = s i n t t f(t)=\frac{sint}{t} f(t)=tsint之类的拉氏变换,当式中s取一些确定的数,可以用来求一些函数的反常积分(广义积分(也就高数上考的最多的积分))
像函数的积分:
∫ s ∞ F ( s ) d s = L [ f ( t ) t ] \int_s^\infty F(s)ds=\mathscr{L}[\frac{f(t)}{t}] ∫s∞F(s)ds=L[tf(t)]
∫ s ∞ d s ∫ s ∞ d s ⋅ ⋅ ⋅ ∫ s ∞ F ( s ) d s = L [ f ( t ) t n ] \int_s^\infty ds\int_s^\infty ds\,···\,\int_s^\infty F(s)ds=\mathscr{L}[\frac{f(t)}{t^n}] ∫s∞ds∫s∞ds⋅⋅⋅∫s∞F(s)ds=L[tnf(t)]
应用:s取一些特殊值时,拉氏变换也可以用来求一些函数的反常积分。
例:求积分 ∫ 0 + ∞ sin t t d t \int_0^{+\infty}\frac{\sin t}{t} dt ∫0+∞tsintdt
即求s = 0时,函数 f ( t ) = s i n t t f(t)=\frac{sint}{t} f(t)=tsint的拉氏变换
已知 sin t 的 像 函 数 为 \sin t的像函数为 sint的像函数为 F [ s ] = L [ s i n t ] = 1 1 + s 2 F[s]=\mathscr{L}[sint]=\frac{1}{1+s^2} F[s]=L[sint]=1+s21
由像函数的积分得
L [ s i n t t ] = ∫ s + ∞ 1 1 + s 2 d s = a r c cot s \mathscr{L}[\frac{sint}{t}]=\int_s^{+\infty}\frac{1}{1+s^2}ds= arc\cot s L[tsint]=∫s+∞1+s21ds=arccots
2.5 延迟性质与位移性质
L [ f ( t − τ ) ] = e − s τ F ( s ) \mathscr{L}[f(t-τ)]=e^{-sτ}F(s) L[f(t−τ)]=e−sτF(s)
L [ e a t f ( t ) ] = ∫ 0 + ∞ e a t f ( t ) e − s t d t = ∫ 0 + ∞ f ( t ) e − ( s − a ) t d t = F ( s − a ) \mathscr{L}[e^{at}f(t)]=\int_0^{+\infty}e^{at}f(t)e^{-st}dt=\int_0^{+\infty}f(t)e^{-(s-a)t}dt=F(s-a) L[eatf(t)]=∫0+∞eatf(t)e−stdt=∫0+∞f(t)e−(s−a)tdt=F(s−a)
应用:顾名思义延迟性质可以用来求 sin ( t − π 2 ) \sin(t-\frac{\pi}{2}) sin(t−2π)之类的拉氏变换,解出来就是辣个答案
三.
基本的数学概念了解了后,再接触一点拉氏变换的物理意义。
我们已经知道傅氏变换将信号分成时域和频域两个方面,而拉氏变换将频率ω变成复频率s,从而不仅能刻画函数的振荡频率,而且还能描述振荡频率的增长(或衰减)速度,这也是拉氏变换和傅氏变换的区别。
s的虚部越大,振荡频率增长得越快。

s的实部越大,波形振荡幅度越大。
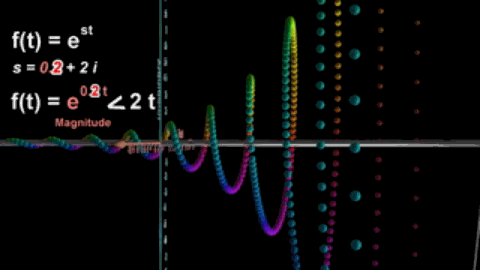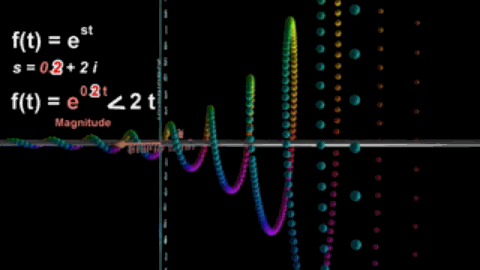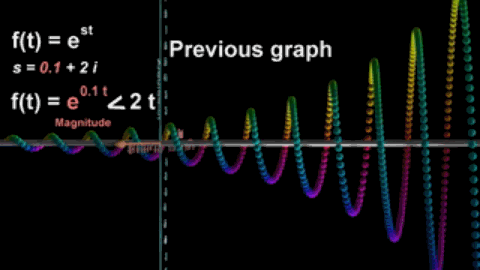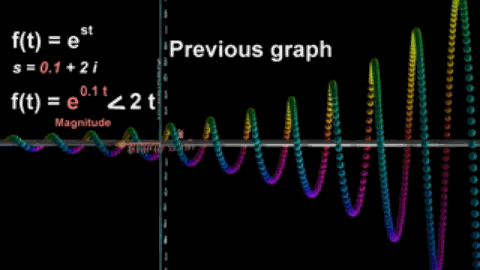
拉氏变换扩大了傅氏变换的适用范围,在数字领域,拉氏变换演变为用于处理离散时间函数或者数字信号的z变换。
References:
[1]复变函数与积分变换(第五版)
[2]直观解释-拉普拉斯变换 https://www.bilibili.com/video/av26328393?from=search&seid=14296184891945561564