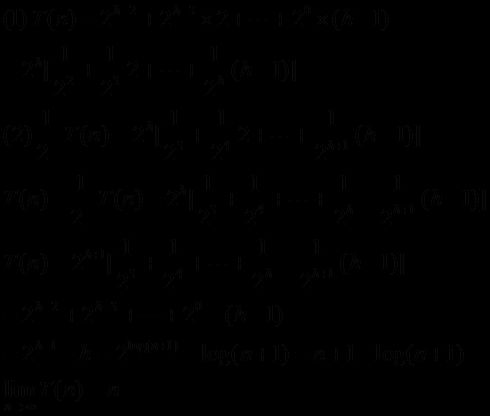二叉堆
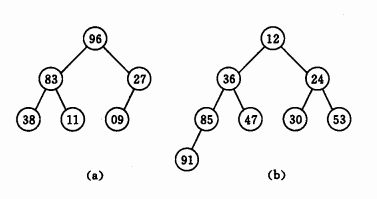
二叉堆也就是数据结构中常说的堆,本质上是一种完全二叉树,在二叉堆中,所有非终端结点的值均不大于(小根堆,图(a)),或不小于(大根堆,图(b))其左右孩子的值。
最大堆,根结点的值为该堆所有结点的最大值。利用堆的此性质,可以实现堆排序。
注意:二叉堆并不是一个二叉排序树。只能保证根节点的值是该堆中所有节点的最值。
根据完全二叉树的性质:结点通常从a[1]开始存储,这样对于下标为k的结点a[k]来说,其左孩子的下标为2*k,右孩子的下标为2*k+1。
- 二叉堆基本操作:
- 1.插入( heapinsert):
void heapinsert(MaxHeap H, int x) { H->data[++H->count] = x; int index = H->count; while (index > 1 && H->data[index/2] < H->data[index]) { swap(H->data[index/2], H->data[index]); index /= 2; } }
- 2.删除大根堆堆顶(heapify):
void heapify(MaxHeap H) { H->data[1] = H->data[H->count--]; int index = 1; while (index * 2 <= H->count) { int left = index * 2; //如果存在右节点,并且右节点大于左节点 if (left + 1 <= H->count&&H->data[left] < H->data[left + 1]) left++; //如果节点已经大于,孩子中较小的节点 if (H->data[index] > H->data[left]) break; swap(H->data[left], H->data[index]); index = left; } }
- 建堆复杂度分析:
给定数组建堆一般有两种方法:
自上而下:
void heapinsert(int *a,int index) { //这里当index=0时,前后都是0,也会停止 while (a[index] > a[(index - 1) / 2]) { swap(a[index], a[(index - 1) / 2]); index = (index - 1) / 2; } } void ArrayToHeap(int *a,int length) { for (int i = 0; i < length; i++) { heapinsert(a, i); } }
自下而上:
void heapify(int *a, int index, int length) { while (index * 2 + 1 <= length) { int left = index * 2 + 1; if (left + 1 <= length - 1 && a[left + 1] < a[left])left++; if (a[index] < a[left])break; swap(a[index], a[left]); index = left; } } void ArrayToBheap(int *a, int length) { int i = length / 2 - 1; for (; i >= 0; i--) { heapify(a, i, length); } }
对于自下而上(从第length/2–1个开始到0,进行heapify),如果仅从代码上直观观察,会得出构造二叉堆的时间复杂度为O(n㏒n)的结果,但这个结果是错的,实际上是O(n)。
对于自上而下(按顺序逐个heapinsert),建堆时间复杂度是O(nlogn)。
证明如下:
假设一个完全二叉树的高度为h,节点的个数为n,现假定完全二叉树为满二叉树:即n = 2^h - 1,h=log(n+1)
那么有2^(h-2)个结点向下访问1次,2^(h-3)个结点向下访问2次,…… 1个结点向下访问h-1次。
(高中的等比数列前n项和公式都忘了-_-)
- 二叉堆的应用:
寻找第K大元素
首先用数组的前k个元素构建一个小根堆,然后遍历剩余数组,就和堆顶比较,如果当前元素大于堆顶,则把当前元素放在堆顶位置,并调整堆(heapify)。
遍历结束后,堆顶就是数组的最大k个元素中的最小值,也就是第k大元素。
K选择
void heapify(int *a, int index, int length) { int left = index * 2 + 1; while (left <= length) { if (left + 1 <= length - 1 && a[left + 1] > a[left])left++; if (a[index] > a[left])break; swap(a[index], a[left]); index = left; } } void ArrayToBheap(int *a, int length) { int i = length / 2 - 1; for (; i >= 0; i--) { Sink(a, i, length); } } void FindKMax(int *a, int k,int length) { ArrayToBheap(a, k); for (int i = k; i < length; i++) { if (a[i] > a[0])a[0] = a[i]; Sink(a, 0, k); } }
随时获取数组中位数:
将数组分成一个大根堆和一个小根堆,始终保持两堆容量差值小于1,比如:完成一个插入后,大根堆有5个元素,小根堆有3个元素,弹出大根堆堆顶。
获取单一中位数时,时间只比传统方法快一点点,但是获取全部的中位数,差距就不是一星半点了。:
float findmedian(int *a,int length) { sort(a, a + length); return (length & 1) ? a[length / 2] : (a[length / 2] + a[length / 2 - 1]) / 2.0; }
代码:
#define MAX 1 #define MIN 2 void heapinsert(int *a, int index,int sign) { if (sign == 1) { while (a[index] > a[(index - 1) / 2]) { swap(a[index], a[(index - 1) / 2]); index = (index - 1) / 2; } } else{ while (a[index] < a[(index - 1) / 2]) { swap(a[index], a[(index - 1) / 2]); index = (index - 1) / 2; } } } void heapify(int *a, int index, int length,int sign) { if (sign == 1) { while (index * 2 + 1 < length) { int left = index * 2 + 1; if (left + 1 < length&&a[left + 1] > a[left])left++; if (a[index] > a[left])break; swap(a[index], a[left]); index = left; } } else { while (index * 2 + 1 < length) { int left = index * 2 + 1; if (left + 1 < length&&a[left + 1] < a[left])left++; if (a[index] < a[left])break; swap(a[index], a[left]); index = left; } } }
float median(int *a,int length) { int *max, *min, maxlength = 1, minlength = 0; max = new int[length]; min = new int[length]; max[0] = a[0]; for (int i = 1; i < length; i++) { if (a[i] > max[0]) { min[minlength] = a[i]; heapinsert(min,minlength++,MIN); } else { max[maxlength] = a[i]; heapinsert(max,maxlength++,MAX); } if (maxlength - minlength == 2) { int t = max[0]; max[0] = max[maxlength - 1]; heapify(max, 0, maxlength - 1,MAX); min[minlength] = t; heapinsert(min, minlength,MIN); maxlength--; minlength++; } else if (minlength - maxlength == 2) { int t = min[0]; min[0] = min[minlength - 1]; heapify(min, 0, minlength - 1,MIN); max[maxlength] = t; heapinsert(max, maxlength,MAX); minlength--; maxlength++; } } return (length & 1) ? (maxlength>minlength?max[0]:min[0]): (max[0] + min[0]) / 2.0; }