Codeforces Round #459 (Div. 2)：D. MADMAX（记忆化搜索+博弈论）

D. MADMAX

time limit per test1 second
memory limit per test256 megabytes

Problem Description

As we all know, Max is the best video game player among her friends. Her friends were so jealous of hers, that they created an actual game just to prove that she’s not the best at games. The game is played on a directed acyclic graph (a DAG) with n vertices and m edges. There’s a character written on each edge, a lowercase English letter.

Max and Lucas are playing the game. Max goes first, then Lucas, then Max again and so on. Each player has a marble, initially located at some vertex. Each player in his/her turn should move his/her marble along some edge (a player can move the marble from vertex v to vertex u if there’s an outgoing edge from v to u). If the player moves his/her marble from vertex v to vertex u, the “character” of that round is the character written on the edge from v to u. There’s one additional rule; the ASCII code of character of round i should be greater than or equal to the ASCII code of character of round i - 1 (for i > 1). The rounds are numbered for both players together, i. e. Max goes in odd numbers, Lucas goes in even numbers. The player that can’t make a move loses the game. The marbles may be at the same vertex at the same time.

Since the game could take a while and Lucas and Max have to focus on finding Dart, they don’t have time to play. So they asked you, if they both play optimally, who wins the game?

You have to determine the winner of the game for all initial positions of the marbles.

Input

The first line of input contains two integers n and m (2 ≤ n ≤ 100, ).

The next m lines contain the edges. Each line contains two integers v, u and a lowercase English letter c, meaning there’s an edge from v to u written c on it (1 ≤ v, u ≤ n, v ≠ u). There’s at most one edge between any pair of vertices. It is guaranteed that the graph is acyclic.

Output

Print n lines, a string of length n in each one. The j-th character in i-th line should be ‘A’ if Max will win the game in case her marble is initially at vertex i and Lucas’s marble is initially at vertex j, and ‘B’ otherwise.

Examples

input
4 4
1 2 b
1 3 a
2 4 c
3 4 b

output
BAAA
ABAA
BBBA
BBBB

input

5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h

output
BABBB
BBBBB
AABBB
AAABA
AAAAB

Note

Here’s the graph in the first sample test case: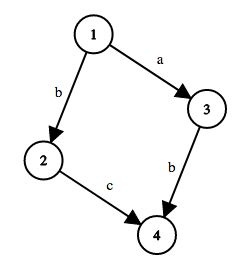

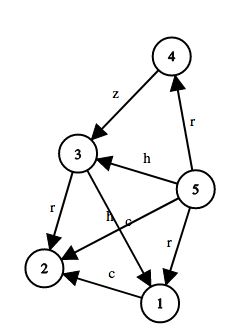
Here’s the graph in the second sample test case:

---

解题心得：

1. 其实是一个简单的记忆化搜索加博弈，难点就是dp需要开一个四维的数组来表示状态，dp[x1][x2][x3][x4]表示A在x1的位置，B在x2的位置，当前行走的路权值至少是x3，该轮到x4走。每次代表一个状态，这也是博弈论相关的思想，不管该怎么走，只要知道在这个状态所代表的输赢关系就可以了。

---

#include 
using namespace std;
const int maxn = 110;
vector int,int> > ve[maxn];
int n,m;
int dp[maxn][maxn][maxn][3];

void init()
{
    memset(dp,-1,sizeof(dp));
    for(int i=0;iint a,b;
        char s[10];
        scanf("%d%d",&a,&b);
        scanf("%s",s);
        int c = s[0] - 'a';
        ve[a].emplace_back(b,c);
    }
}

int dfs(int x,int y,int va,int turn)
{
    if(dp[x][y][va][turn] != -1)
        return dp[x][y][va][turn];
    if(turn == 0)//该A走
    {
        for(int i=0;iint, int> v = ve[x][i];
            if (v.second >= va)
                if (dfs(v.first, y, v.second, 1 - turn) == 0)
                    return dp[x][y][va][turn] = 0;
        }
        return dp[x][y][va][turn] = 1;
    }
    else
    {
        for(int i=0;iint,int> v = ve[y][i];
            if(v.second >= va)
                if(dfs(x,v.first,v.second,1 - turn) == 1)
                    return dp[x][y][va][turn] = 1;
        }
        return dp[x][y][va][turn] = 0;
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    init();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(dfs(i,j,-1,0))
                printf("B");
            else
                printf("A");
        }
        printf("\n");
    }
    return 0;
}

转载于:https://www.cnblogs.com/GoldenFingers/p/9107187.html