R-CNN/Selective-Search
Rigion Proposal开山之作,其实网上已经有很多博客了,但是都是就其理论说明,没有很好的直观展示,有时候概念性的东西比较不容易脑补,晦涩难懂。
首先,给出代码出处:
import selectivesearch
#如果没有此库,pip install selectivesearch 安装
SS算法第一步需要进行的是图像分割,即大名鼎鼎的felzenszwalb算法,下面先就这个算法进行讲解:
其实在这个算法里有这么几个可调参数,sigma,k,kernel,min_size,其中,sigma和kernel是GaussianBlur的参数
首先理解无向图:
图是若干个顶点(Vertices)和边(Edges)相互连接组成的。边仅由两个顶点连接,并且没有方向的图称为无向图。一说到图就可能涉及到深度优先算法和广度优先算法,这里就不做说明,具体的都可以百度到。
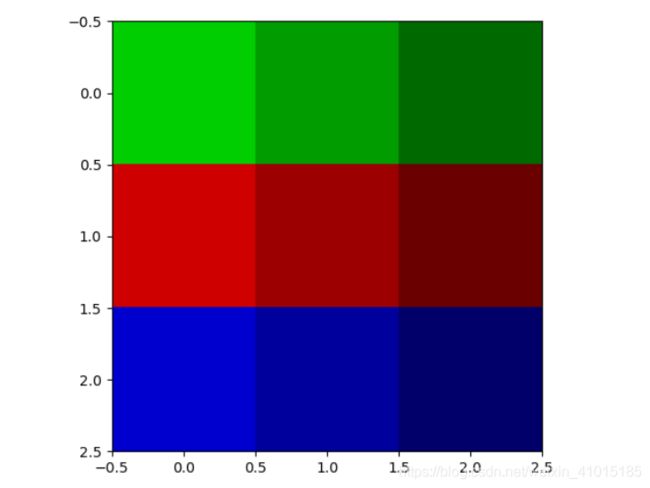
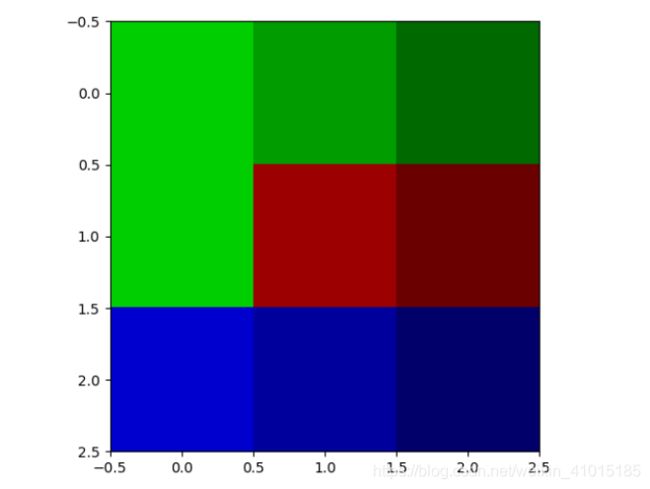
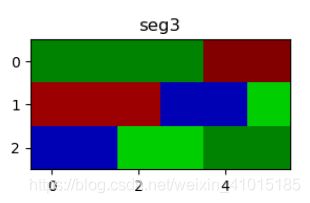
假设我给出了两个图像(3x3x3),记为图像A和B,左A,右B,为了后面好说明问题,如下图所示:
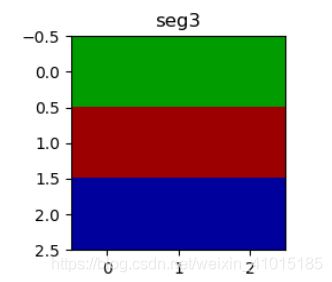
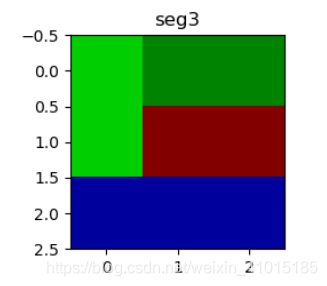
我们就对这两个图像进行图像分割,这里先贴出分割后的结果,左图C是A的结果,右图D是B的结果:
如下图是对建立无向图的边的一些简单说明:
这里假设了一些数据,这些数据就是上图A和B的数据,因为是3x3的矩阵,所以一共生成了24个边,每个边标记了连接的像素节点和和像素节点间的距离,图中已经给出了计算方式,有了这些数据后,开始建立无向图,先贴出代码:
#mini_size = 3; 也可以设置成2,可以看下效果
# 构建无向图(树)
class universe(object):
def __init__(self, n, k):
self.f = np.array([i for i in range(n)]) # 树
# [0 1 2 3 4 5 6 7 8]
self.r = np.zeros_like(self.f) # root
# [0 0 0 0 0 0 0 0 0]
self.s = np.ones((n)) # 存储像素点的个数
# [1. 1. 1. 1. 1. 1. 1. 1. 1.]
self.t = np.ones((n)) * 60 # 存储不相似度 这里50是k值,为了容易理解,就直接写60
# [1. 1. 1. 1. 1. 1. 1. 1. 1.]
self.k = k
def find(self, x): # Find root of node x
if x == self.f[x]:
return x
return self.find(self.f[x])
def join(self, a, b): # Join two trees containing nodes n and m
if self.r[a] > self.r[b]:
self.f[b] = a
self.s[a] += self.s[b]
else:
self.f[a] = b
self.s[b] += self.s[a]
if self.r[a] == self.r[b]:
self.r[b] += 1
u = universe(num, k)
#第一个循环
for edge in edges:
a, b = u.find(int(edge[0])), u.find(int(edge[1]))
if ((a != b) and (edge[2] <= min(u.t[a], u.t[b]))):
# 更新类标号:将类a,b标号统一为的标号a。更新该类的不相似度阈值为:k / (u.s[a]+u.s[b])
u.join(a, b)
a = u.find(a)
u.t[a] = edge[2] + k / u.s[a]
#第二个循环
for edge in edges:
a, b = u.find(int(edge[0])), u.find(int(edge[1]))
if ((a != b) and ((u.s[a] < min_size) or u.s[b] < min_size)):
# 分割后会有很多小区域,当区域像素点的个数小于min_size时,选择与其差异最小的区域合并
u.join(a, b)
那么这段代码具体说了个什么意思呢?就是我先将这个edges矩阵按照距离方式从小到大排列,那么我总是按照最小的距离值进行搜索,这里就用到图的概念了,下面举一个比较直观的例子,定义为图E:
我们先要根据像素点(节点)找到它的标号也就是代码中的a和b值,图E的例子是 (15, 14, 0),这个距离是最小的,为0,如果a!=b 且距离<=t中的不相似度阈值,t的更新计算公式如代码,有个超参数k是可调的,则合并像素点,并且在f中进行标记,那么这是f的值为[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 14 16 17],且在14的位置进行root标记,r的结果为[0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0],存储该位置的像素点的个数
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1.],不相似度矩阵t的结果为[50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 0.5 50. 50. 50. ],合并14和15像素点。
下一个边为(14,15,0),因为已经被标记过了跳过计算;
下一个边为(1,0,50),前提是能从14和15找到1,0吗,显然不行,所以要另起炉灶,将1和0像素点合并,f的值为[ 0 0 2 3 4 5 6 7 8 9 10 11 12 13 14 14 16 17],r的值为[1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0],s的值为[2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1.],t的值为[50.5 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 0.5 50. 50. 50. ]
下一个边为(2,1,50),因为此时节点1和0节点是相连的了,所以a和b的值为(2,0),合并0和1和2像素,这里我直接给出值:
[ 0 0 0 3 4 5 6 7 8 9 10 11 12 13 14 14 16 17]
[1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0]
[3. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1.]
[50.33333333 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 0.5 50. 50. 50. ]
下一个边为(3,2,50),这里我们看一下,3没有与任何节点相连,2与节点0相连,那么a和b的值为(3,0),满足合并条件继续合并,也直接给出值:
[ 0 0 0 0 4 5 6 7 8 9 10 11 12 13 14 14 16 17]
[1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0]
[4. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 1. 1. 1.]
[50.25 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 50. 0.5 50. 50. 50. ]
下一个边为(5. 4. 50),这里5和4显然没有与任何节点相连,那么又要另起炉灶了,满足和并条件合并,这里就下不给值了,我们往下看
下一个边为(7,6,50),这里7和6显然没有与任何节点相连,那么又要另起炉灶了,满足和并条件合并
下一个边为(8,7,50),7显然与6相连,那么a和b的值为(8,6),合并6,7,8像素
下一个边为(10,9,50),另起炉灶合并
下一个边为(13,12,50),另起炉灶合并
[50.25 50. 50. 50. 50.5 50. 50.33333333 50. 50. 50.5 50. 50. 50.5 50. 0.5 50. 50. 50. ]
下一个边为(16,15,50),14与15已经合并,那么a和b的值为(16,14),等下貌似符合合并条件,但是,别忘了还有个min(t[a],t[b]),14位置的不相似度阈值已经是0.5了,所以50大于0.5,当然也不满足合并条件楼
下一个边为(17,16,50),这两个边都没有标记过,那么我们就讲究凑合着合并吧
下一个边是(0,1,50),显然0和1已经连接过了,a和b的值为(0,0),那么不符合a!=b的条件,统统放弃
至此所有的像素合并结束,其实就是按图索骥。。。,这个例子似乎一直是从左到右的在合并,其实上下也在进行,只不过要看左右上下的距离排序,图B就是先合并的上下。
#########################################
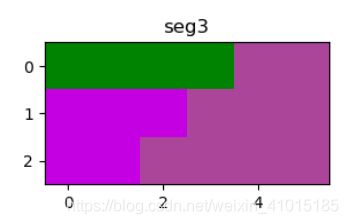
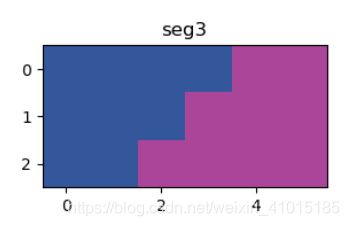
此时来到第二个循环,一句话理解,分割后会有很多的小区域,当区域像素点的个数小于min_size时,选择与其差异最小的区域合并,用图说话,图E设置了min_size为2,效果如上,如果将min_size设置为3呢
设置为4和100呢,100就成了一个颜色了,设置成1和2的效果是一样的
至此,图像分割算法就完成了,接着往下走,这次就拿真实图片来讲,左边是真实图片,右边是分割完的图片,直接是selectivesearch里面产生的效果:
下面进入另一个函数,
def _extract_regions(img):区域合并采取了多样性的策略,如果简单采用一种策略很容易错误合并不相似区域,比如只考虑纹理,不同颜色的区域很容易被错误合并,选择性搜索采用三种多样性策略来增加候选区域以保证找回;1.多种颜色空间,考虑RGB,灰度,HSV及其变种;2.多种相似度度量标准,即考虑颜色相似度,又考虑纹理、大小、重叠情况;3.通过改变阈值初始化原始区域,阈值越大,分割的区域越少。
由RBG颜色空间到HSV颜色空间
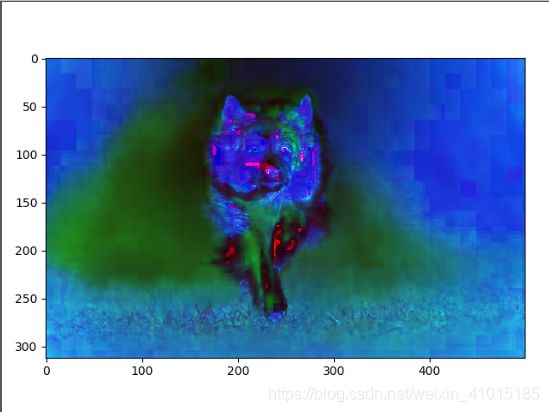
计算texture_gradient,效果如图:
区域相似度计算:
颜色相似度:使用L1-normalize归一化获取每个颜色通道的25bins的直方图,这样每个区域都可以得到一个75维的向量,具体请看代码
def _calc_colour_hist(img):纹理相似度计算:这里纹理采用SIFT-LIKE特征,具体做法是对每个颜色通道的8个不同方向计算方差 delt = 1的高斯微分,使用L1-normalize归一化获取图像每个颜色通道的每个方向的10bins的直方图,这样就可以获取到一个240(10x8x3)维的向量,区域间纹理相似度与颜色相似度计算类似。具体请看代码
def _calc_texture_hist(img):
区域合并:
优先合并小的区域,如果仅仅是通过颜色和纹理特征合并的话,很容易使合并后的区域不断吞噬周围的区域,后果就是多尺度只应用在了那个局部,而不是全局的多尺度。因此我们给小的区域更多的权重,这样保证在图像每个位置都是多尺度合并。
代码:
def _sim_size(r1, r2, imsize):
"""
calculate the size similarity over the image
"""
return 1.0 - (r1["size"] + r2["size"]) / imsize如果区域ri包含在rj内,我们首先应该合并,另一方面,如果ri和rj相接,他们之间会形成断崖,不应该合并在一块。这里定义区域的合适度距离主要是为了衡量两个区域是都更加吻合,其指标是合并后的bounding box越小,其相似度越近,代码中是bbsize
代码:
def _sim_fill(r1, r2, imsize):
"""
calculate the fill similarity over the image
"""
bbsize = (
(max(r1["max_x"], r2["max_x"]) - min(r1["min_x"], r2["min_x"]))
* (max(r1["max_y"], r2["max_y"]) - min(r1["min_y"], r2["min_y"]))
)
return 1.0 - (bbsize - r1["size"] - r2["size"]) / imsize合并四种相似度:
代码:
def _calc_sim(r1, r2, imsize):
return (_sim_colour(r1, r2) + _sim_texture(r1, r2)
+ _sim_size(r1, r2, imsize) + _sim_fill(r1, r2, imsize))完毕!!关于直方图可视化后续再加上吧!!!