【算法】全排列(有重复、无重复)多解
全排列问题主要就是在递归上,我们只要对每一层压栈和出栈搞清楚,相信理解起来全排列是没有问题的
有重复元素的全排列
方法一:借助swap回溯
算法思想:通过swap函数,先换一种排列方式,在递归进去,排下一次的顺序。然后拍完之后,重新返还到当前的栈帧中,在通过swap来帮我们还原到之前的顺序排列。
代码实现:
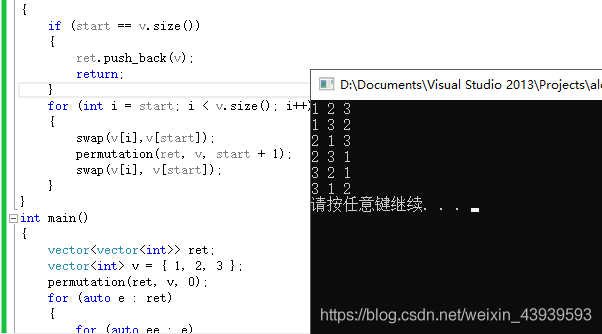
void permutation(vector<vector<int>>& ret ,vector<int>& v,int start)
{
if(start == v.size())
{
ret.push_back(v);
return;
}
for(int i = start; i < v.size(); i++)
{
swap(v[i],v[start]);
permutation(ret,v,start+1); //继续递归。知道start == v.size()
swap(v[i],v[start]);
}
}
int main ()
{
vector<vector<int>> ret;
vector<int> v = {1,2,3};
permutation(ret,v,0);
for(auto e: ret)
{
for(auto ee: e)
{
cout << ee << " ";
}
cout << endl;
}
system("pause");
}
- 对string对象的全排列也类似,只是没有给出例子。
- 这种方法最终的结果,有重复,只是我们的测试用例没有给出重复的用例
方法二 借助pop_back回溯
【算法思想】:所有的全排列都是对递归的使用。之所以与方法一不一样,是因为当string或者vector进行全排列的时候,它可以借助pop_back()这个函数,来进行状态的还原。更重要的是,我们还需要用一个数组vector< bool >型的数组标记每个元素是否可以取,取过的则跳过不取这个元素。
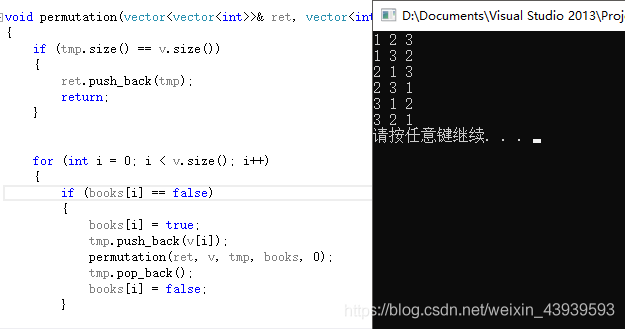
void permutation(vector<vector<int>>& ret, vector<int>& v, vector<int> tmp, vector<bool>& books)
{
if (tmp.size() == v.size())
{
ret.push_back(tmp);
return;
}
for (int i = 0; i < v.size(); i++)
{
if (books[i] == false) //如果books[i]为false代表还没有选择,可以选择
{
books[i] = true; // 将标志改为true,等会递归的时候不能在选择v[i]
tmp.push_back(v[i]); // 添加进tmp数组
permutation(ret, v, tmp, books); //继续递归调用
tmp.pop_back(); // 递归出来,还原原来的状态,将添加进去的v[i] pop出来
books[i] = false; // 标志位改为可以访问的状态
}
}
}
int main()
{
vector<vector<int>> ret;
vector<int> v = { 1, 2, 3 };
vector<int> tmp;
vector<bool> books(v.size(), false);
permutation(ret, v, tmp, books);
for (auto e : ret)
{
for (auto ee : e)
{
cout << ee << " ";
}
cout << endl;
}
system("pause");
}
- 对string对象的全排列也类似,只是没有给出例子。
- 这种方法最终的结果,有重复,只是我们的测试用例没有给出重复的用例
方法三 一种全排列的模板
无重复元素的全排列
方法一: 利用set去重优化
算法思想:
对有重复的上述两种方法进行改进,加入set< string > 对象,自动去重,这样子,我们就可以选出无重复元素的全排列。如果字符串的数量很多的话,set效率有点低。
那我们也可以用unordered_set做一个备忘录,如果在备忘录中的话,我们就可以查找出来,这样的话我们就不加入进vector
代码实现:
void permutation(set<vector<int>>& ret, vector<int>& v, vector<int> tmp,vector<bool>& books, int start) //存进set中
{
if (tmp.size() == v.size())
{
ret.insert(tmp);
return;
}
for (int i = 0; i < v.size(); i++)
{
if (books[i] == false)
{
books[i] = true;
tmp.push_back(v[i]);
permutation(ret, v, tmp, books, 0);
tmp.pop_back();
books[i] = false;
}
}
}
int main()
{
set<vector<int>> ret;
vector<int> v = {1, 1,1, 3 };
vector<int> tmp;
vector<bool> books(v.size(), false);
permutation(ret, v, tmp, books, 0);
for (auto e : ret)
{
for (auto ee : e)
{
cout << ee << " ";
}
cout << endl;
}
system("pause");
}
- 我们用set< vector< int>> 的set集合,set自带去重,加入进set的都是独一无二的数组。所以这个是对上面的有重复的进行优化
- 但是set还得调用insert函数,代价性能会随着数据的增多而过大
方法二:回溯过程中去重
算法思想:
先将要全排列的数组先sort()排好序以后,我们根据重复值a[i] == a[i-1]和 看之前的重复值是否被访问过,决定是否要用这个值。
代码实现:
int a[4] = { 1,1,3,4};
bool vis[4] = { false };
int cnt = 0;
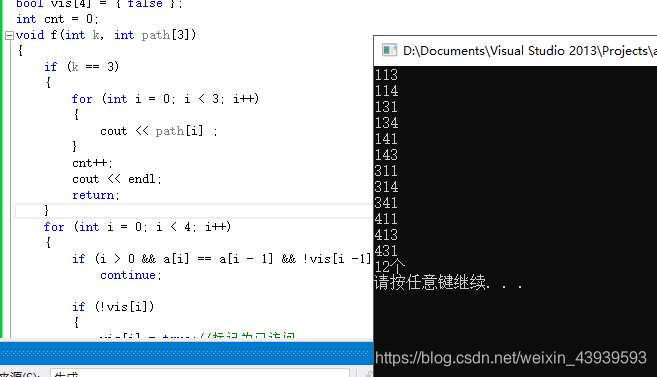
void f(int k, int path[3]) // 一共4个数,选出三个进行全排列
{
if (k == 3)
{
for (int i = 0; i < 3; i++)
{
cout << path[i] ;
}
cnt++;
cout << endl;
return;
}
for (int i = 0; i < 4; i++)
{
if (i > 0 && a[i] == a[i - 1] && !vis[i -1]) // 现在选取的元素和上一个相同,上一个元素还没有被使用
continue;
if (!vis[i]) //vis[i]为false的时候,!vis[i] = true, 所以进入循环
{
vis[i] = true; //标记为已访问
path[k] = a[i]; //将k的位置填入数据
f(k + 1, path); //递归
vis[i] = false; //还原状态
}
}
}
int main()
{
int path[3];
f(0, path);
cout << cnt << "个" << endl;
system("pause");
}
- 如果没有加上去重语句的话,就是24个
方法三:使用库函数next_permutation
算法思想:
对于vector和string对象可以使用库函数next_permutation来完成全排列。但是next_permutation有一个限制条件:在全排列之前,数组或者字符串必须是有序的,所以我们得在使用库函数next_permutation之前 sort()排序。
代码实现:
int main()
{
vector<int> v = { 1,1,1,4 };
sort(v.begin(), v.end());
do{
for (auto&e : v)
{
cout << e << " ";
}
cout << endl;
} while (next_permutation(v.begin(),v.end())); //限制条件,在做这个之前必须是有序的
system("pause");
}
- 我们可以看出来是无重复的,打印出来的都是独一无二的。(对于string类型也是一样的)
- next_permutation是库里的,经过高度优化过的,肯定比我们自己写的无重复全排列的效率高很多。emm,有一次oj中用这个函数可以过90%,而自己写的全排列才可以过50%