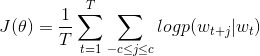猫咪爱柠檬

word2vec原理学习笔记

目录

学习词向量的意义

使用神经网络学习词向量的基本思路

word2vec主要思路

skip-gram预测

CBOW预测

softmax函数

模型训练

Skip-gram

CBOW

梯度下降

计算参数向量的梯度

负采样（Negative Sample）

本文由学习参考资料等材料后，本着容易理解的原则进行整理后形成。

学习词向量的意义

中文中的词语含义博大精深，例如：

他说：“她这个人真有意思（funny）。”她说：“他这个人怪有意思的（funny）。”于是人们以为他们有了意思（wish），并让他向她意思意思（express）。他火了：“我根本没有那个意思（thought）！”她也生气了：“你们这么说是什么意思（intention）？”事后有人说：“真有意思（funny）。”也有人说：“真没意思（nonsense）”。（原文见《生活报》1994.11.13.第六版）［吴尉天，1999］ ——《统计自然语言处理》

词是自然语言处理中最小单位。词向量出现之前，词语使用词表长度的one-hot向量来表示，词表越大，词向量越大，且这些向量并没有词语意思的表示。因为他们是正交的，所以无法通过任何运算得到相似度。

motel:[ 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 ]

hotel: [ 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 ]

$motel\cdot hotel^T = 0$

提出：语言学家J.R.Firth提出，通过一个单词的上细纹可以得到他的意思。这是现代统计自然语言处理最成功的思想之一。

通过向量定义词语的含义，即通过调整一个单词及其上下文单词的向量，是的根据这两个向量可以推测这两个词语的相似度；或根据向量可以预测词语的上下文。这种手法也是递归的，根据向量来调整向量，与词典中意向的定义相似。

意义：通过词向量可以推辞或近似得到两个词语的相似性，即给词向量一个“意思”，而非一个简单的表示。

使用神经网络学习词向量的基本思路

定义一个可以预测某个单词的上下文模型：

损失函数定义如下：

$J = 1-p(w_{-t}|w_t)$

这里的 $w_{-t}$ 表示的上下文，如果完美预测，损失函数为零。

然后在一个大型语料库的不同位置得到训练实例，调整词向量，最小化损失函数。

word2vec主要思路

两种主要方法，通过上下文预测中心词或通过中心词预测上下文。

skip-gram预测

通过中心词预测上下文

CBOW预测

Continuous Bag of Words：通过上下文预测中心词

两种提高训练效率的方法：

Hierarchical softmax:层次softmax
Negative sampling:负采样

softmax函数

从实数空间到概率分布的标准映射方法。指数函数可以把实数映射成正数，然后归一化得到概率。

$p_i =\frac{e^{u_i}}{\sum_{j}e^{u_i}}$

softmax之所以叫softmax，是因为指数函数会导致较大的书变得更大，小的数变得更小；这种选择作用类俗语max函数。

模型训练

Skip-gram

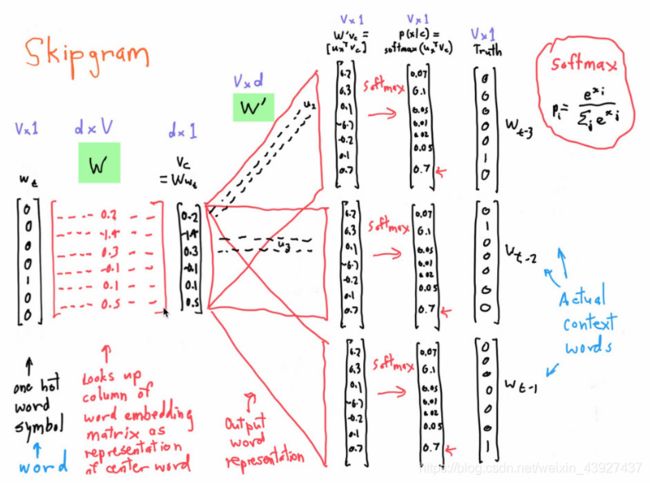
这张图很便于过程理解，所以直接贴过来了。从最左边的one-hot向量，乘以center word的,找到词向量，乘以另一个context word的矩阵得到每个词语的“相似度”，对相似度取softmax得到概率，与答案对比计算损失。抄原文，写的太清楚了。和是需要我们学习的参数。

skip-gram模型是根据中中心词预测上下文词出现的概率。记上图中的为 $W^{(1)}$ ，为 $W^{(2)}$ ，具体步骤如下：

生成中心词one-hot向量
得到上下文的词的输入向量 $u^i = W^{(1)}x$
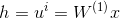
设置为 $h = u^i = W^{(1)}x$
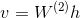根据 $v = W^{(2)}h$ 生成2C个分数向量， $v^{i-C}, ......,v^{i-1}, v^{i+1},......,v^{i+C}$
将每个词的得分转化为概率，

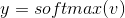
同样的，将生成的概率与真实上下文的词进行对比，希望得到匹配的结果。

与CBOW的目标函数不同，Skip-gram使用了贝叶斯假设来推到概率，假设条件独立。换句话说，他的上下文之间的关系是独立的。我们可以得到优化函数：

$minimize J = -logP(w^{i-C},...,w^{i-1}, w^{i+1},...,w^{i+C}|w^{i}) \\ = -log \prod_{j=0,j\neq C}^{2C} P(w^{(i-C+j)}|w^{i}) \\ = -log \prod_{j = 0,j \neq C}^{2C} P(v^{(i-c+j)}|u^{i}) \\ = -log \prod_{j = 0,j \neq C}^{2C} \frac{exp(v^{(i-c+j)T}u^{(i)})}{\sum_{k = 1}^{|V|}exp(v^{(k)T}u^{(i)})} \\ = -\sum_{j=0,j \neq C}^{2C} v^{(i-c+j)T}u^{(i)} + 2Clog\sum_{k=1}^{|V|} exp(v^{(k)T}u^{(i)})$

在每次迭代中，通过计算梯度更新未知参数。

CBOW

模型步骤分解如下：

1. 对敞口大小为C的上下文，生成one-hot矩阵 $(x^{(i-C)}, ..., x^{(x-1)}, x^{(i+1)},...,x^{(i+C)})$

2. one-hot向量左乘输入矩阵 $W^{(1)}$ ,即可得到上下文的词向量 $(u^{(i-C)} = W^{(1)}x^{(i-C)}, u^{(i-C+1)} = W^{(1)}x^{(i-C+1)},...,u^{(i+C)} = W^{(1)}x^{(i+C)})$

3. 对上下文的词向量求平均 $h=\frac{u^{(i-C)}+...+u^{(i+C)}}{2C}$

4. 根据输入矩阵 $W^{(2)}$ 生成得分向量 $z=W^{(2)}h$

5. 将得分转化为概率， $\hat{y} = softmax(z)$

怎样学习参数 $W^{(1)}$ 和 $W^{(2)}$ 呢？

首先创建爱你目标函数，从真实概率分布中学习未知概率分布，通常会根据信息论从中选择两个分布的距离度量函数，最常用的是交叉上函数：

$H(\hat{y},y) = -\sum_{j=1}^{|V|}y_ilog(\hat{y}_j)$

由于y是one-hot向量，所以上面的式子可以简化为

$H(\hat{y},y) = -y_ilog(\hat{y}_j)$

因为是1，所以优化目标为：

$minimizeJ = -log P(w^{(i)}|w^{(i-C)},...,w^{(i-1)},w^{(i+1)}, ..., w^{(i+C)}) \\ = -log P(v^{(i)}|h) \\ = -log \frac{exp(v^{(i)T} h)}{\sum_{j=1}^{|V|}exp(v^{(i)T} u^{(j)})} \\ =-exp(v^{(i)T} h) +log\sum_{j=1}^{|V|}exp(v^{(i)T} u^{(j)})$

接下来就可以采用梯度下降优化目标函数。

这里解释一下为什么可以用交叉熵作为目标函数？如果预测准确， $\hat{y} = 1$ ，我们可以计算损失，也就是交叉熵 $H(\hat{y},y) = -1log(1) = 0$ ；如果预测不准确，假设 $\hat{y} = 0.01$ ，交叉熵 $H(\hat{y},y) = -1log(0.01)\approx 4.605$ ，所以，对于概率分布的距离，交叉熵有很好的表现。

梯度下降

把所有的参数写入向量 $\theta$ ，对d维的词向量和大小为V的词表来讲，有：

由于有两个矩阵，所以 $\theta$ 的维度中有个2.。

在整个训练数据上计算损失函数 $J(\theta)$ 的最小化，需要对所有窗口计算一下梯度：

$\theta_j^{new} = \theta_j^{old} - \alpha {\frac{\partial }{\partial \theta_j^{old}}} J(\theta) \\$

$\theta_j^{new} = \theta_j^{old} - \alpha \bigtriangledown_\theta J(\theta)$

上面是梯度下降的优化方法。然而通常训练集会很大，也许有几亿的单词，更新一次就需要耗费很长的时间训练，所以使用随机梯度下降（Stochastic Gradient Descent）来计算参数，核心是每个窗口t后更新参数，公式就变为

$\theta_j^{new} = \theta_j^{old} - \alpha \bigtriangledown_\theta J_t(\theta)$

神经网络喜欢嘈杂的算法，这可能是SGD成功的另一个原因。

在计算每个窗口时，最多有个词，所以梯度是很稀疏的，我么你只需要更新出现的词的向量。有两种方法：

1. 对每个词向量做hash；

2. 只更新输入词向量矩阵和输出词向量矩阵的指定列（即词所在的那列）

最重要的一点，如果我么你有百万级别的词向量要计算，最好使用分布式方式。

计算参数向量的梯度

以skip-gram为例

对于大小为c的窗口，预测目标词的上下文可能出现的词，目标函数为

$J(\theta) = \frac{1}{T} \sum_{t=1}^{T} \sum_{-c \le j \le c} logp(w_{t+j}|w_t)$

即，最大化给定中心词后的任意上下文概率。对于 $p(w_{t+j}|w_j)$ 最简单的公式为：

$p(w_O | w_I) = \frac{exp(u_{O}^T v_I)}{\sum_{w=1}^{W} exp(u_w^T v_I)}$

这就是softmax函数形式，其中和分别表示词的输入向量和输出向量（每个词有两个向量，这点和那重要！）

想要优化目标函数，我么你需要对公式求导求梯度，在推到过程中，两个知识点需要掌握：

矩阵求导 $\frac{\partial X^T a }{\partial X} = \frac{\partial a^T X}{\partial X} = a$
链式法则 $\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}$

对概率p求导

$\frac{\partial p(o|c)}{\partial v_c} = \frac{\partial }{\partial v_c} log(\frac{exp(u_o^T v_c)}{\sum_{w=1}^W exp(u_w^Tv_c)}) \\ = {\frac{\partial }{\partial v_c}}(log(exp(u_O^Tv_c))-log(\sum_{w=1}^Wexp(u_w^Tv_c))) \\ =u_o- \frac{1}{\sum_{w=1}^W exp(u_w^Tv_c)}\frac{\partial }{\partial v_c}\sum_{w=1}^W exp(u_w^Tv_c) \\ = u_o-\frac{1}{\sum_{w=1}^W exp(u_w^Tv_c)}\sum_{x=1}^{W}\frac{\partial }{\partial v_c}exp(u_x^Tv_c) \\ = u_o - \frac{1}{\sum_{w=1}^W exp(u_w^Tv_c)}\sum_{x=1}^{W}exp(u_x^T v_c)u_x \\ = u_o - \sum_{x=1}^{W}\frac{exp(u_x^T v_c)}{\sum_{w=1}^{W}exp(u_w^T v_c)}u_x \\ =u_o-\sum_{x=1}^{W}p(x|c) u_x$

第二项是一个期望：所有上下文词向量乘以他们的概率之和，所以就等于观测值减去期望值

为了便于理解，附上常用的求导公式：

$y = log_a x \Rightarrow {y}' = \frac{1}{xlna} \\$

$y = e^x \Rightarrow {y}' = e^x \\$

$y = lnx \Rightarrow {y}' = \frac{1}{x}$

第三步中，用x代替了w，防止与前面求和的w混淆。

负采样（Negative Sample）

无论是Skip-gram还是CBOW模型，其实都是分类模型。对于机器学习中的分类任务，在训练的时候不但要给正例，还要给负例。对于Hierarchical Softmax，负例是二叉树的其他路径。对于Negative Sampling，负例是随机挑选出来的。据说Negative Sampling能提高速度、改进模型质量。

以上两种目标函数可以发现，在迭代过程中，需要计算真个词汇表的和，而词的个数通常在百万级，所以需要花费巨大的计算时间。一个简单的做法是可以对全部词汇做近似。

在每个训练步骤中，只采样几个负样本代替遍历整个词汇及。按照词频排序的分布中采样，把上述的公式和负采样结合在一起。我们只需要更新：

目标函数
梯度
更新法则

NS方法是Mikolov et al.在论文Distribution Representations of Words and Phrases and Their Compositionality 中提出的。NS事实上优化的是不同于上面的目标函数。存在一个中心词和上下文词对，用表示该词来自训练集，表示词不在训练集。首先，使用sigmod函数对概率P建模：

$P(D=1|w,c,\theta) = \frac{1}{1+exp(-v_c^T v_w)}$

然后，建立一个目标函数，来最大化出现在训练集中的词对的概率和没有出现在训练集的词对的概率。我们采用简单的最大似然来计算，这里 $\theta$ 就是模型中的未知参数，也就是上面模型中的 $W^{(1)}$ 和 $W^{(2)}$

$\theta = argmax_\theta \prod_{(w,c) \in D} P(D=1|w,c, \theta) \prod_{(w,c) \notin D} P(D=0 |w,c, \theta) \\ = argmax_\theta \prod_{(w,c) \in D} P(D=1|w,c, \theta) \prod_{(w,c) \notin D} (1-P(D=0 |w,c, \theta))$

$log\theta = argmax_\theta \sum_{(w,c) \in D} logP(D=1|w,c,\theta) + \sum_{(w,c) \notin D} log(1-P(D=1|w,c,\theta)) \\ = argmax_\theta \sum_{(w,c) \in D} log \frac{1}{1 + exp(-v_c^T v_w)} + \sum_{(w,c) \notin D} log(1 - \frac{1}{1+exp(-v_c^T v_w)}) \\ = argmax_\theta \sum_{(w,c) \in D} log \frac{1}{1 + exp(-v_c^T v_w)} + \sum_{(w,c) \notin D} log \frac{1}{1+ exp(v_c^T w_w)}$

其中， ${(w,c) \notin D}$ 表示负样本的采样。那么，我们的目标函数就变成了：

$-log \sigma(v^{(i-C+j)}\cdot h) + \sum_{k=1}^K log \sigma(\breve{v}^{(k)} \cdot h)$

其中， $\breve{v}^{(k)}|k=1...K$ 表示从分布采样的个负样本。

关于什么样的分布能够是的近似效果最好的讨论有很多，常用的方法是一元模型值去3/4次方，3/4次方能够是的低频词的采样效率被提高。

参考资料：

https://blog.csdn.net/pirage/article/details/84931180

http://www.hankcs.com/nlp/word-vector-representations-word2vec.html

你可能感兴趣的:(自然语言处理)

UNDERSTANDING HTML WITH LARGE LANGUAGE MODELS liferecords LLM 语言模型人工智能自然语言处理
UNDERSTANDINGHTMLWITHLARGELANGUAGEMODELS相关链接：arXiv关键字：大型语言模型、HTML理解、Web自动化、自然语言处理、机器学习摘要大型语言模型（LLMs）在各种自然语言任务上表现出色。然而，它们在HTML理解方面的能力——即解析网页的原始HTML，对于自动化基于Web的任务、爬取和浏览器辅助检索等应用——尚未被充分探索。我们为HTML理解模型（经过微调
ChatGPT技巧大揭秘：AI写代码新境界 2401_83550420 chatgpt4.0 chatgpt chatgpt 人工智能 AI写作
ChatGPT无限次数:点击直达ChatGPT技巧大揭秘：AI写代码新境界随着人工智能技术的不断进步，开发人员现在有了更多有趣的工具来提高他们的工作效率。其中，ChatGPT作为一种基于深度学习的自然语言处理模型，已经成为许多开发者的新宠。在本文中，我们将揭秘使用ChatGPT来帮助编写代码的技巧，探索AI在编程领域的新境界。ChatGPT简介ChatGPT是一种基于大型神经网络的对话生成模型，它
AI大模型学习：开启智能时代的新篇章游向大厂的咸鱼人工智能学习
随着人工智能技术的不断发展，AI大模型已经成为当今领先的技术之一，引领着智能时代的发展。这些大型神经网络模型，如OpenAI的GPT系列、Google的BERT等，在自然语言处理、图像识别、智能推荐等领域展现出了令人瞩目的能力。然而，这些模型的背后是一系列复杂的学习过程，深度学习技术的不断演进推动了AI大模型学习的发展。首先，AI大模型学习的基础是深度学习技术。深度学习是一种模仿人类大脑结构的机器
【循环神经网络rnn】一篇文章讲透 CX330的烟花 rnn 人工智能深度学习算法 python 机器学习数据结构
目录引言二、RNN的基本原理代码事例三、RNN的优化方法1长短期记忆网络（LSTM）2门控循环单元（GRU）四、更多优化方法1选择合适的RNN结构2使用并行化技术3优化超参数4使用梯度裁剪5使用混合精度训练6利用分布式训练7使用预训练模型五、RNN的应用场景1自然语言处理2语音识别3时间序列预测六、RNN的未来发展七、结论引言众所周知，CNN与循环神经网络（RNN）或生成对抗网络（GAN）等算法结
ChatGPT神技：AI成为你的编程良友 2401_83481083 chatgpt4.0 chatgpt chatgpt 人工智能 AI写作
ChatGPT无限次数:点击直达ChatGPT神技：AI成为你的编程良友近年来，人工智能技术的发展迅猛，ChatGPT作为其中一项创新技术，正逐渐走进我们的生活。在编程领域，AI不仅可以助力我们提高效率，还能成为我们的良友，帮助解决各种编程难题。一、ChatGPT简介ChatGPT是一种基于自然语言处理技术的人工智能模型，它能够生成类人对话。ChatGPT通过深度学习模型，能够理解输入的文本并生成
智合同如何助力建筑行业合同智能化管理智合同（小智）合同智能应用 AI技术降本增效提质人工智能自然语言处理知识图谱深度学习大数据
#建筑行业#人工智能#AI#合同智能应用#深度学习#自然语言处理技术#知识图谱智合同-采用深度学习、自然语言处理技术、知识图谱等人工智能技术，为企业提供专业的合同相关的智能服务。其主要服务包含：合同智能审查、合同要素智能提取、合同版本对比、合同智能起草、ICR智能识别、合同履约追踪、文本一致性对比、广告审查、合同范本库等服务。智合同在助力建筑行业合同智能化管理方面具有显著的优势。首先，智合同利用A
GEE在灾害预警中的遥感云大数据应用及GPT模型辅助分析 AIzmjl GPT 生态遥感大数据 gpt gee 灾害预警水体湿地遥感
随着遥感技术的快速发展，云大数据在灾害、水体与湿地领域的应用日益广泛。通过遥感云大数据，我们能够实时获取灾害发生地的影像信息，为灾害预警、应急响应提供有力支持。同时，在水体与湿地监测方面，遥感云大数据也发挥着重要作用，帮助我们了解水体的分布、变化以及湿地的生态状况。近年来，GPT模型在自然语言处理领域取得了显著成果，其强大的文本生成和理解能力为遥感云大数据的应用提供了新的可能。通过将GPT模型与遥
自然语言处理概念以及发展黑夜照亮前行的路自然语言处理
自然语言概念总结自然语言处理（NaturalLanguageProcessing，简称NLP）是计算机科学领域与人工智能领域的一个重要方向，它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。自然语言处理旨在帮助计算机理解和处理自然语言，使计算机能够像人类一样处理和生成语言。从概念上讲，自然语言处理融合了语言学、计算机科学和数学等多学科的知识。它并不仅仅是一般地研究自然语言，而是侧重
什么是分布式搜索引擎罗彬桦分布式搜索引擎搜索引擎分布式
什么是分布式搜索引擎搜索引擎所谓搜索引擎，就是根据用户需求与一定算法，运用特定策略从互联网检索出制定信息反馈给用户的一门检索技术。搜索引擎依托于多种技术，如网络爬虫技术、检索排序技术、网页处理技术、大数据处理技术、自然语言处理技术等，为信息检索用户提供快速、高相关性的信息服务。搜索引擎技术的核心模块一般包括爬虫、索引、检索和排序等，同时可添加其他一系列辅助模块，以为用户创造更好的网络使用环境。分布
自然语言处理（NLP）技术的概念及优势刘小董学习心得自然语言处理
自然语言处理（NLP）是人工智能领域的一个重要分支，其目标是使计算机能够理解、处理和生成人类自然语言的形式和含义。NLP技术的优势包括：实现人机交互：NLP技术可以使计算机与人类之间实现自然的语言交互，使人们可以通过语音识别、语义理解等方式与计算机进行交流。大规模文本处理：NLP技术可以对大规模文本进行自动化处理和分析，提取关键信息和知识，从而实现文本分类、情感分析、信息检索等任务。自动化翻译：N
大型语言模型RAG（检索增强生成）：检索技术的应用与挑战 in_tsz 语言模型人工智能自然语言处理
摘要检索增强生成（RAG）系统通过结合传统的语言模型生成能力和结构化数据检索，为复杂的问题提供精确的答案。本文深入探讨了RAG系统中检索技术的工作原理、实现方式以及面临的挑战，并对未来的发展方向提出了展望。随着大型预训练语言模型（LLMs）如GPT-3和BERT的出现，自然语言处理（NLP）领域取得了显著进展。然而，这些模型在处理知识密集型任务时仍存在局限性，特别是在需要最新或特定领域知识的情况下
AI人工智能小程序系统开发修行者对666 安卓gradle android adb
开发AI人工智能小程序系统需要以下步骤：1.确定需求：了解客户对人工智能小程序的期望，并分析系统的实际应用场景。2.设计架构：选择合适的技术框架和人工智能算法，进行小程序系统架构的设计。3.数据采集和处理：收集必要的数据，并进行预处理和特征提取，为人工智能算法提供支持。4.开发算法模型：根据需求和设计，开发相应的算法模型，如自然语言处理、图像识别等。5.实现小程序功能：将算法模型集成到小程序系统中
NLP技术小天才dhsb 网络其他
自然语言处理（NLP）技术可以应用在多个领域，例如机器翻译、情感分析、文本分类等。以下是几个例子：1.机器翻译：NLP技术可以将一种语言的文本自动翻译成另一种语言。例如，谷歌翻译就是应用了NLP技术，它可以将英语的文本翻译成其他语言，如法语、西班牙语等。2.情感分析：NLP技术可以分析文本中的情感倾向。例如，通过分析社交媒体上用户的评论和推文，可以判断用户对某个产品或事件的情感态度是正面的、负面的
【AI视野·今日NLP 自然语言处理论文速览第八十二期】Tue, 5 Mar 2024 hitrjj LLM NLP Papers 人工智能自然语言处理 NLP 预训练模型文本摘要情绪识别推理训练
AI视野·今日CS.NLP自然语言处理论文速览Tue,5Mar2024(showingfirst100of175entries)Totally100papers上期速览✈更多精彩请移步主页DailyComputationandLanguagePapersKey-Point-DrivenDataSynthesiswithitsEnhancementonMathematicalReasoningAut
Transformer、BERT和GPT 自然语言处理领域的重要模型 Jiang_Immortals 人工智能自然语言处理 transformer bert
Transformer、BERT和GPT都是自然语言处理领域的重要模型，它们之间有一些区别和联系。区别：架构：Transformer是一种基于自注意力机制的神经网络架构，用于编码输入序列和解码输出序列。BERT（BidirectionalEncoderRepresentationsfromTransformers）是基于Transformer架构的双向编码模型，用于学习上下文无关的词向量表示。GP
大语言模型可信性浅谈 MarkHD 语言模型人工智能自然语言处理
大语言模型可信性的研究摘要：随着人工智能技术的快速发展，大语言模型在自然语言处理领域的应用越来越广泛。然而，大语言模型的可信性一直是人们关注的焦点。本文将从多个维度探讨大语言模型的可信性问题，包括模型性能、数据质量、隐私保护等方面，并提出相应的解决方案。一、引言大语言模型是指能够处理大规模文本数据的深度学习模型，如BERT、GPT等。这些模型在自然语言处理任务中取得了显著的成果，包括文本分类、情感
ChatGPT介绍程序媛9688 gpt
ChatGPT概述ChatGPT是一种前沿的大型语言模型（LargeLanguageModel,LLM），由人工智能研究组织OpenAI研发并推出。它基于Transformer架构，这是一种在自然语言处理（NLP）领域取得突破的深度学习方法。通过在海量的互联网文本数据上进行预训练，ChatGPT获得了强大的语言理解和生成能力。语言理解能力ChatGPT能够理解和分析复杂的自然语言文本。无论是用户提
Python中的自然语言处理和文本挖掘 api77 电商api api python 自然语言处理 easyui 开发语言网络前端 java
在Python中，自然语言处理（NLP）和文本挖掘通常涉及对文本数据进行清洗、转换、分析和提取有用信息的过程。Python有许多库和工具可以帮助我们完成这些任务，其中最常用的包括nltk（自然语言处理工具包）、spaCy、gensim、textblob和scikit-learn等。以下是一个简单的例子，展示了如何使用Python和nltk库进行基本的自然语言处理和文本挖掘。安装必要的库首先，确保你
Transformer结构介绍和Pyotrch代码实现肆十二 Pytorch语法 transformer 深度学习人工智能
Transformer结构介绍和Pyotrch代码实现关注B站查看更多手把手教学：肆十二-的个人空间-肆十二-个人主页-哔哩哔哩视频(bilibili.com)基本结构介绍Transformer结构是近年来自然语言处理（NLP）领域的重要突破，它完全基于注意力机制（AttentionMechanism）来实现，克服了传统RNN模型无法并行计算以及容易丢失长距离依赖信息的问题。Transformer
【探索AI】四：AI（人工智能）自然语言处理（NLP）美少女战士1@ 学习笔记 AI 人工智能自然语言处理
自然语言处理（NLP）的概念自然语言处理（NaturalLanguageProcessing，NLP）是一门交叉学科，涉及人工智能、计算机科学和语言学等领域，旨在让计算机能够理解、分析、生成和处理人类语言。NLP技术致力于使计算机能够与人类以自然语言进行交流，从而实现更加智能、便捷的人机交互。在自然语言处理中，常见的任务包括但不限于：文本分类：将文本按照预定义的类别进行分类，如垃圾邮件分类、新闻分
ChatGPT 4.0：革新文献检索与推荐体验 chatgpt
ChatGPT4.0：革新文献检索与推荐体验随着信息时代的到来，学术文献的数量急剧增加，如何快速而准确地检索到所需的文献，以及发现潜在有价值的研究，成为了学术界的一大挑战。ChatGPT4.0作为最新一代的自然语言处理模型，不仅在文献检索方面展现出强大的能力，更是在文献推荐领域发挥着越来越重要的作用。文献检索：精准、快速、深入ChatGPT4.0在文献检索方面的优势主要体现在三个方面：精准性、速度
Phoncent：开启AI创作与学习的新时代庄泽峰人工智能 gpt AIGC AI写作
随着人工智能技术的飞速发展，我们生活中的许多方面都正在经历着深刻的变革。在这个大背景下，Phoncent平台的出现，无疑为我们提供了一个全新的、一站式的AI创作与学习体验。Phoncent的核心优势在于其深度整合了GPT技术。GPT，作为一种先进的大型语言模型，已经在自然语言处理领域展现出了惊人的能力。它能够理解并生成人类语言，为我们提供了与机器进行自然、流畅交流的可能性。在Phoncent平台上
深度学习的进展 CuiXg 深度学习人工智能
深度学习的进展深度学习作为人工智能领域的重要分支之一，利用神经网络模拟人类大脑的学习过程，通过数据训练模型以自动提取特征、识别模式、进行分类和预测等任务。近年来，深度学习在多个领域取得显著进展，尤其在自然语言处理、计算机视觉、语音识别和机器翻译等方面实现了突破性进展。方向一：深度学习的基本原理和算法深度学习基于神经网络概念，涉及反向传播、卷积神经网络、循环神经网络等算法。这些算法模拟人脑神经元间的
Attention注意力机制 xieyan0811
网上的文章总把Attention注意力机制和Transformer模型结合来讲，看起来非常复杂。实际上Attention不仅作用于自然语言处理领域，目前已是很通用的技术。本篇来看看Attention的原理，以及在各个领域的典型应用。原理越来越多的模型用到注意力机制，它已成为与全连接，卷积，循环网络同等重要的技术。简单地说，当人观察图片时，一般先扫一眼，确定大概信息，然后聚焦在图中的重要区域，这个区
掌握Python编程与ChatGPT的强强联手：开启人工智能助手新时代快乐非自愿 python chatgpt 人工智能
本文将介绍如何利用Python编程语言和ChatGPT技术实现强强联手，以打造功能强大的人工智能助手。我们将探讨Python编程在ChatGPT应用中的重要性，并展示如何利用Python与ChatGPT共同构建一个智能对话系统。最后，我们将探讨如何将这一技术应用于实际场景，为用户提供高效、实用的解决方案。随着人工智能技术的不断发展，自然语言处理（NLP）已经成为当今科技领域的热点。在众多NLP技术
探索卷积神经网络的奇妙世界-JSP hkmaike cnn 人工智能神经网络
卷积神经网络（ConvolutionalNeuralNetworks，CNNs）是一种深度学习模型，被广泛用于图像识别、语音识别、自然语言处理等领域。它的特殊结构使得它在处理具有空间结构的数据时表现出色。本文将深入介绍卷积神经网络的原理、应用和未来发展方向。卷积神经网络的基本结构卷积神经网络的核心是卷积层（ConvolutionalLayer）。卷积层通过滤波器（Filter）在输入数据上进行滑动
【人工智能学习思维脉络导图】 AK@ 人工智能人工智能学习
曾梦想执剑走天涯，我是程序猿【AK】目录知识图谱1.基础知识2.人工智能核心概念3.实践与应用4.持续学习与进展5.挑战与自我提升6.人脉网络知识图谱人工智能学习思维脉络导图1.基础知识计算机科学基础数学基础（线性代数、微积分、概率论和统计学）编程语言（Python、R等）2.人工智能核心概念机器学习监督学习无监督学习强化学习深度学习神经网络卷积神经网络（CNN）循环神经网络（RNN）自然语言处理
合槽位填充技术的问答系统构建步骤及其所需的技术和工具 Komorebi_9999 知识图谱问答系统自然语言处理
下面是结合槽位填充技术的问答系统构建步骤及其所需的技术和工具：1.知识图谱构建技术/工具：Neo4j或ArangoDB（图数据库）RDF2Neo（将RDF数据导入Neo4j的工具）D2RQ（将关系型数据库转化为SPARQL端点）模型算法：资源描述框架（RDF）Web本体语言（OWL）2.自然语言处理（NLP）技术/工具：spaCy（用于文本处理、词性标注、命名实体识别等）NLTK或HuggingF
【无标题】 Komorebi_9999 知识图谱问答系统自然语言处理
要构建一个基于知识图谱的问答系统，你需要进行以下工作：知识图谱构建：数据采集：从各种来源（如公开数据库、API、网页等）收集与你的领域相关的数据。数据清洗和预处理：清洗数据，去除重复、错误或不相关的信息，对数据进行归一化、标准化处理。实体识别和关系抽取：从数据中识别出实体（如人、地点、概念等）和它们之间的关系。构建图谱：将实体和关系组织成图谱结构，通常使用图数据库来存储。自然语言处理（NLP）：分
人工智能出海业务：快速发展的新趋势金鸣识别人工智能 ocr 图像处理机器学习目标检测神经网络视觉检测
随着全球人工智能技术的持续进步和应用领域的不断拓展，人工智能在海外市场的出海业务正呈现出蓬勃发展的势头。从美国硅谷到中国北京中关村，从欧洲伦敦到新加坡科技园，越来越多的人工智能企业纷纷将目光投向海外，寻求更广阔的市场空间和更多的商业机会。人工智能技术的快速发展为企业的出海提供了有力支撑。人工智能在图像识别、自然语言处理、智能驾驶等领域取得了显著进展，为企业走出国门打下了坚实基础。越来越多的人工智能
算法单链的创建与删除换个号韩国红果果 c 算法
先创建结构体 struct student { int data; //int tag;//标记这是第几个 struct student *next; }; // addone 用于将一个数插入已从小到大排好序的链中 struct student *addone(struct student *h,int x){ if(h==NULL) //??????
《大型网站系统与Java中间件实践》第2章读后感白糖_ java中间件
断断续续花了两天时间试读了《大型网站系统与Java中间件实践》的第2章，这章总述了从一个小型单机构建的网站发展到大型网站的演化过程---整个过程会遇到很多困难，但每一个屏障都会有解决方案，最终就是依靠这些个解决方案汇聚到一起组成了一个健壮稳定高效的大型系统。看完整章内容，
zeus持久层spring事务单元测试 deng520159 java DAO spring jdbc
今天把zeus事务单元测试放出来,让大家指出他的毛病, 1.ZeusTransactionTest.java 单元测试 package com.dengliang.zeus.webdemo.test; import java.util.ArrayList; import java.util.List; import org.junit.Test; import
Rss 订阅开发周凡杨 html xml 订阅 rss 规范
RSS是 Really Simple Syndication的缩写（对rss2.0而言，是这三个词的缩写，对rss1.0而言则是RDF Site Summary的缩写，1.0与2.0走的是两个体系）。 RSS
分页查询实现 g21121 分页查询
在查询列表时我们常常会用到分页，分页的好处就是减少数据交换，每次查询一定数量减少数据库压力等等。按实现形式分前台分页和服务器分页：前台分页就是一次查询出所有记录，在页面中用js进行虚拟分页，这种形式在数据量较小时优势比较明显，一次加载就不必再访问服务器了，但当数据量较大时会对页面造成压力，传输速度也会大幅下降。服务器分页就是每次请求相同数量记录，按一定规则排序，每次取一定序号直接的数据
spring jms异步消息处理 510888780 jms
spring JMS对于异步消息处理基本上只需配置下就能进行高效的处理。其核心就是消息侦听器容器，常用的类就是DefaultMessageListenerContainer。该容器可配置侦听器的并发数量，以及配合MessageListenerAdapter使用消息驱动POJO进行消息处理。且消息驱动POJO是放入TaskExecutor中进行处理，进一步提高性能，减少侦听器的阻塞。具体配置如下：
highCharts柱状图布衣凌宇 hightCharts 柱图
第一步：导入 exporting.js,grid.js,highcharts.js;第二步：写controller @Controller@RequestMapping(value="${adminPath}/statistick")public class StatistickController { private UserServi
我的spring学习笔记2-IoC（反向控制依赖注入） aijuans spring mvc Spring 教程 spring3 教程 Spring 入门
IoC（反向控制依赖注入）这是Spring提出来了，这也是Spring一大特色。这里我不用多说，我们看Spring教程就可以了解。当然我们不用Spring也可以用IoC，下面我将介绍不用Spring的IoC。 IoC不是框架，她是java的技术，如今大多数轻量级的容器都会用到IoC技术。这里我就用一个例子来说明：如：程序中有 Mysql.calss 、Oracle.class 、SqlSe
TLS java简单实现 antlove java ssl keystore tls secure
1. SSLServer.java package ssl; import java.io.FileInputStream; import java.io.InputStream; import java.net.ServerSocket; import java.net.Socket; import java.security.KeyStore; import
Zip解压压缩文件百合不是茶 Zip格式解压 Zip流的使用文件解压
ZIP文件的解压缩实质上就是从输入流中读取数据。Java.util.zip包提供了类ZipInputStream来读取ZIP文件,下面的代码段创建了一个输入流来读取ZIP格式的文件; ZipInputStream in = new ZipInputStream(new FileInputStream(zipFileName)); &n
underscore.js 学习（一） bijian1013 JavaScript underscore
工作中需要用到underscore.js，发现这是一个包括了很多基本功能函数的js库，里面有很多实用的函数。而且它没有扩展 javascript的原生对象。主要涉及对Collection、Object、Array、Function的操作。学
java jvm常用命令工具——jstatd命令(Java Statistics Monitoring Daemon) bijian1013 java jvm jstatd
1.介绍 jstatd是一个基于RMI（Remove Method Invocation）的服务程序，它用于监控基于HotSpot的JVM中资源的创建及销毁，并且提供了一个远程接口允许远程的监控工具连接到本地的JVM执行命令。 jstatd是基于RMI的，所以在运行jstatd的服务
【Spring框架三】Spring常用注解之Transactional bit1129 transactional
Spring可以通过注解@Transactional来为业务逻辑层的方法(调用DAO完成持久化动作)添加事务能力，如下是@Transactional注解的定义： /* * Copyright 2002-2010 the original author or authors. * * Licensed under the Apache License, Version
我(程序员)的前进方向 bitray 程序员
作为一个普通的程序员,我一直游走在java语言中,java也确实让我有了很多的体会.不过随着学习的深入,java语言的新技术产生的越来越多,从最初期的javase,我逐渐开始转变到ssh,ssi,这种主流的码农,.过了几天为了解决新问题,webservice的大旗也被我祭出来了,又过了些日子jms架构的activemq也开始必须学习了.再后来开始了一系列技术学习,osgi,restful.....
nginx lua开发经验总结 ronin47
使用nginx lua已经两三个月了，项目接开发完毕了，这几天准备上线并且跟高德地图对接。回顾下来lua在项目中占得必中还是比较大的，跟PHP的占比差不多持平了，因此在开发中遇到一些问题备忘一下 1：content_by_lua中代码容量有限制，一般不要写太多代码，正常编写代码一般在100行左右（具体容量没有细心测哈哈，在4kb左右），如果超出了则重启nginx的时候会报 too long pa
java-66-用递归颠倒一个栈。例如输入栈{1,2,3,4,5}，1在栈顶。颠倒之后的栈为{5,4,3,2,1}，5处在栈顶 bylijinnan java
import java.util.Stack; public class ReverseStackRecursive { /** * Q 66.颠倒栈。 * 题目：用递归颠倒一个栈。例如输入栈{1,2,3,4,5}，1在栈顶。 * 颠倒之后的栈为{5,4,3,2,1}，5处在栈顶。 *1. Pop the top element *2. Revers
正确理解Linux内存占用过高的问题 cfyme linux
Linux开机后，使用top命令查看，4G物理内存发现已使用的多大3.2G，占用率高达80%以上： Mem: 3889836k total, 3341868k used, 547968k free, 286044k buffers Swap: 6127608k total,&nb
[JWFD开源工作流]当前流程引擎设计的一个急需解决的问题 comsci 工作流
当我们的流程引擎进入IRC阶段的时候，当循环反馈模型出现之后，每次循环都会导致一大堆节点内存数据残留在系统内存中，循环的次数越多，这些残留数据将导致系统内存溢出，并使得引擎崩溃。。。。。。而解决办法就是利用汇编语言或者其它系统编程语言，在引擎运行时，把这些残留数据清除掉。
自定义类的equals函数 dai_lm equals
仅作笔记使用 public class VectorQueue { private final Vector<VectorItem> queue; private class VectorItem { private final Object item; private final int quantity; public VectorI
Linux下安装R语言 datageek R语言 linux
命令如下：sudo gedit /etc/apt/sources.list1、deb http://mirrors.ustc.edu.cn/CRAN/bin/linux/ubuntu/ precise/ 2、deb http://dk.archive.ubuntu.com/ubuntu hardy universesudo apt-key adv --keyserver ke
如何修改mysql 并发数(连接数)最大值 dcj3sjt126com mysql
MySQL的连接数最大值跟MySQL没关系，主要看系统和业务逻辑了方法一：进入MYSQL安装目录打开MYSQL配置文件 my.ini 或 my.cnf查找 max_connections=100 修改为 max_connections=1000 服务里重起MYSQL即可　　方法二：MySQL的最大连接数默认是100客户端登录：mysql -uusername -ppass
单一功能原则 dcj3sjt126com 面向对象的程序设计软件设计编程原则
单一功能原则[ 编辑] SOLID 原则单一功能原则开闭原则 Liskov代换原则接口隔离原则依赖反转原则查论编在面向对象编程领域中，单一功能原则（Single responsibility principle）规定每个类都应该有
POJO、VO和JavaBean区别和联系 fanmingxing VO POJO javabean
POJO和JavaBean是我们常见的两个关键字，一般容易混淆，POJO全称是Plain Ordinary Java Object / Plain Old Java Object，中文可以翻译成：普通Java类，具有一部分getter/setter方法的那种类就可以称作POJO，但是JavaBean则比POJO复杂很多，JavaBean是一种组件技术，就好像你做了一个扳子，而这个扳子会在很多地方被
SpringSecurity3.X--LDAP：AD配置 hanqunfeng SpringSecurity
前面介绍过基于本地数据库验证的方式，参考http://hanqunfeng.iteye.com/blog/1155226，这里说一下如何修改为使用AD进行身份验证【只对用户名和密码进行验证，权限依旧存储在本地数据库中】。将配置文件中的如下部分删除：
mac mysql 修改密码 IXHONG mysql
$ sudo /usr/local/mysql/bin/mysqld_safe –user=root & //启动MySQL(也可以通过偏好设置面板来启动)$ sudo /usr/local/mysql/bin/mysqladmin -uroot password yourpassword //设置MySQL密码（注意，这是第一次MySQL密码为空的时候的设置命令，如果是修改密码，还需在-
设计模式--抽象工厂模式 kerryg 设计模式
抽象工厂模式：工厂模式有一个问题就是，类的创建依赖于工厂类，也就是说，如果想要拓展程序，必须对工厂类进行修改，这违背了闭包原则。我们采用抽象工厂模式，创建多个工厂类，这样一旦需要增加新的功能，直接增加新的工厂类就可以了，不需要修改之前的代码。总结：这个模式的好处就是，如果想增加一个功能，就需要做一个实现类，
评"高中女生军训期跳楼” nannan408
首先，先抛出我的观点，各位看官少点砖头。那就是，中国的差异化教育必须做起来。孔圣人有云：有教无类。不同类型的人，都应该有对应的教育方法。目前中国的一体化教育，不知道已经扼杀了多少创造性人才。我们出不了爱迪生，出不了爱因斯坦，很大原因，是我们的培养思路错了，我们是第一要“顺从”。如果不顺从，我们的学校，就会用各种方法，罚站，罚写作业，各种罚。军
scala如何读取和写入文件内容？ qindongliang1922 java jvm scala
直接看如下代码： package file import java.io.RandomAccessFile import java.nio.charset.Charset import scala.io.Source import scala.reflect.io.{File, Path} /** * Created by qindongliang on 2015/
C语言算法之百元买百鸡 qiufeihu c 算法
中国古代数学家张丘建在他的《算经》中提出了一个著名的“百钱买百鸡问题”，鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一，百钱买百鸡，问翁，母，雏各几何？代码如下： #include <stdio.h> int main() { int cock,hen,chick; /*定义变量为基本整型*/ for(coc
Hadoop集群安全性：Hadoop中Namenode单点故障的解决方案及详细介绍AvatarNode wyz2009107220 NameNode
正如大家所知，NameNode在Hadoop系统中存在单点故障问题，这个对于标榜高可用性的Hadoop来说一直是个软肋。本文讨论一下为了解决这个问题而存在的几个solution。 1. Secondary NameNode 原理：Secondary NN会定期的从NN中读取editlog，与自己存储的Image进行合并形成新的metadata image 优点：Hadoop较早的版本都自带，

按字母分类： A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 其他